2.2 Система геодезических координат

1. Геодезическая широта - угол , образованный нормалью к поверхности эллипсоида в данной точке и плоскостью экватора.

2. Геодезическая долгота - двугранный угол , образованный плоскостью меридиана , где расположена точка М, с плоскостью начального меридиана (рис. 2.1).

2.3 Главные радиусы кривизны в данной точке эллипсоида

Рис. 2.2

Через нормаль к поверхности эллипсоида можно провести бесчисленное множество плоскостей.

Эти плоскости, перпендикулярные касательной плоскости к поверхности эллипсоида в данной точке, называются нормальными.

Кривые, образуемые от пересечения нормальных плоскостей с поверхностью эллипсоида, называются нормальными сечениями.

Из множества нормальных сечений в данной точке эллипсоида М можно выделить два главных сечения:

Меридианное сечение - сечение, проходящее через данную точку и оба полюса. На рис. 2.2 оно представлено эллипсом .

Сечение первого вертикала - сечение, проходящее через точку М и перпендикулярное меридианному эллипсу. На рис. 2.2 оно представлено кривой .

Радиус кривизны меридиана в данной точке М определяется выражением:

. (2.4)

С возрастанием широты радиус М увеличивается. Так на экваторе (В = 0°) он равен

,

а на полюсе (В = 90°)

.

Радиус кривизны первого вертикала в данной точке М, вычисляется по формуле:

. (2.5)

Из (2.5) следует, что на экваторе (В = 0°) он будет

,

а на полюсе (В = 90°)

.

Средний радиус кривизны в данной точке М равен среднему геометрическому величин М и N, т.е.

, (2.6)

который на экваторе принимает значение:

,

а на полюсе равен

.

И наконец радиус кривизны произвольного нормального сечения, заданного азимутом А, может быть определен из выражения:

. (2.7)

2.4 Длина дуги меридиана

1. Длина дуги меридиана от экватора до точки с широтой В вычисляется по формуле:

, (2.8)

где

(2.9)

Численные значения констант в (2.9) приведены для эллипсоида Красовского.

2. Если ожидаемая длина дуги меридиана между двумя точками с широтой В₁ и В₂ не превышает 450 км, ее точную длину с погрешностью не более 1 см можно вычислить по приближенной формуле:

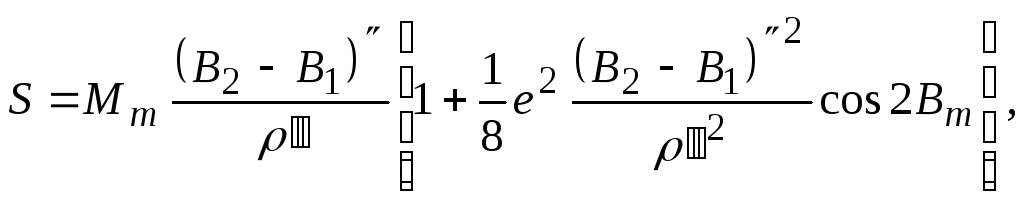(2.10)

где , - радиус кривизны меридиана на широте .

Если ожидаемая длина дуги не более 45 км, ее точную длину можно

вычислить по приближенной формуле:

(2.11)

2.5 Длина дуги параллели

Длина дуги параллели на широте , при разности долгот крайних точек этой дуги , дается формулой:

(2.12)

2.6 Площадь сфероидической трапеции, ограниченной дугами меридианов и параллелей

(2.13)

где

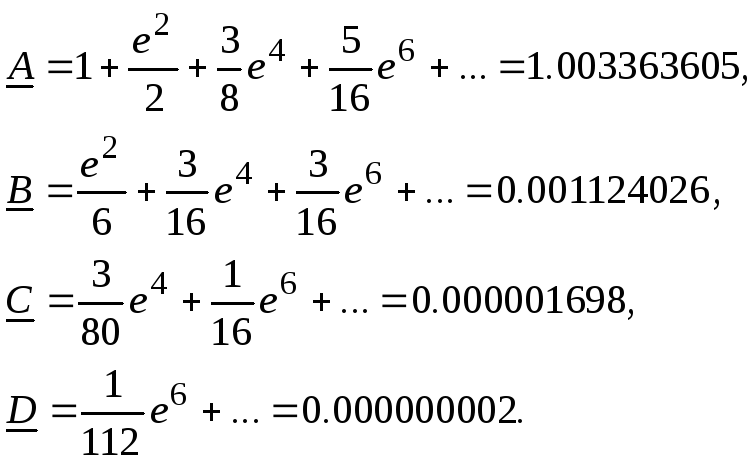(2.14)

Численные значения в выражениях (2.14) приведены для эллипсоида Красовского.

2.7 Вычисление плоских прямоугольных координат х и у в проекции Гаусса по геодезическим координатам В и L

Для вычисления плоских конформных координат в проекции Гаусса по известным геодезическим координатам В и L служат формулы:

(2.15)

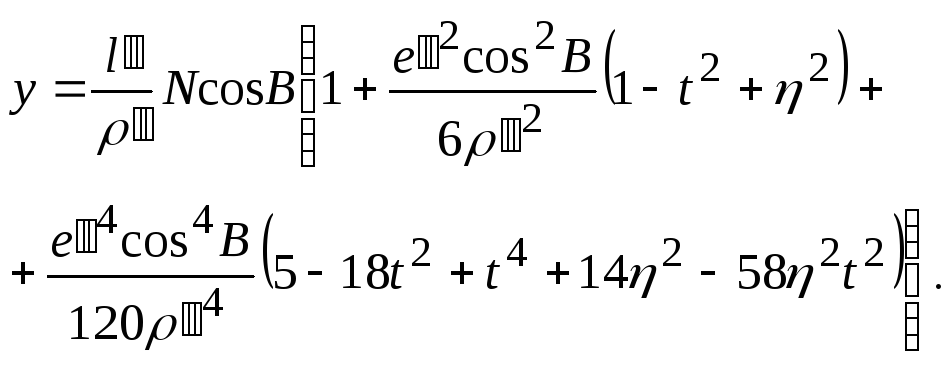(2.16)

В формулах (2.15) и (2.16) приняты обозначения:

- длина дуги меридиана от экватора до точки с широтой В;

- разность долгот данной точки и осевого меридиана;

2.8 Сближение меридианов

Сближение меридианов на плоскости в проекции Гаусса выражается довольно сложной формулой. Однако с погрешностью порядка на краю шестиградусной зоны на широте 50° его можно определить по приближенной формуле:

(2.17)

2.9 Переход от расстояний на эллипсоиде к расстояниям на плоскости в проекции Гаусса

Названный выше переход может быть осуществлен в первом приближении умножением длины дуги меридиана или параллели на масштабный коэффициент:

(2.18)

где - средняя ордината линии; R_m - средний радиус кривизны для данной линии.

2.10 Изображение эллипсоида на шаре

При картографировании значительных территорий в масштабе 1:1000 000 и мельче целесообразно и вполне допустимо пренебречь сжатием земного эллипсоида и принять Землю за шар. В этом случае задача сводится к определению радиуса шара R .

Как решается поставленная задача?

Единого решения не существует. Все зависит от того, каким шаром мы хотим заменить эллипсоид. Рассмотрим несколько наиболее типичных случаев.

1. Шар имеет поверхность, одинаковую с поверхностью эллипсоида. В этом случае:

2. Если же мы хотим, чтобы шар имел объем, равный объему эллипсоида, то

3. При изображении некоторой части земной поверхности на плоскости удобно заменить эллипсоид шаром, радиус которого равен среднему радиусу кривизны R, который равен согласно (3.7):

4. Если мы хотим, чтобы длина меридиана на шаре была равна длине меридиана на эллипсоиде, то согласно(2.9) принимаем:

5. Если мы хотим получить равновеликое изображение на шаре для любого широтного пояса, то принимаем , а сферические координаты и точек на шаре вычисляем по геодезическим координатам, используя формулы:

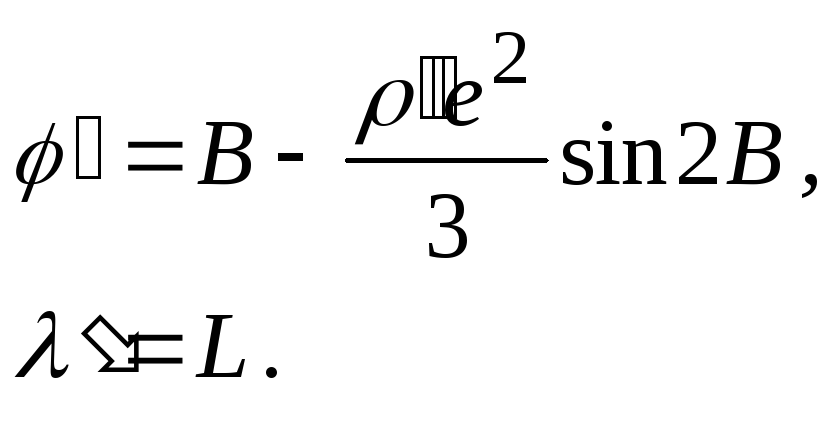(2.19)

6. Если мы хотим, чтобы при изображении земного эллипсоида на шаре сохранялись без искажения углы между любыми направлениями, т.е. чтобы получилось равноугольное изображение, радиус шара принимают равным большой полуоси эллипсоида , а сферические координаты получают из выражений:

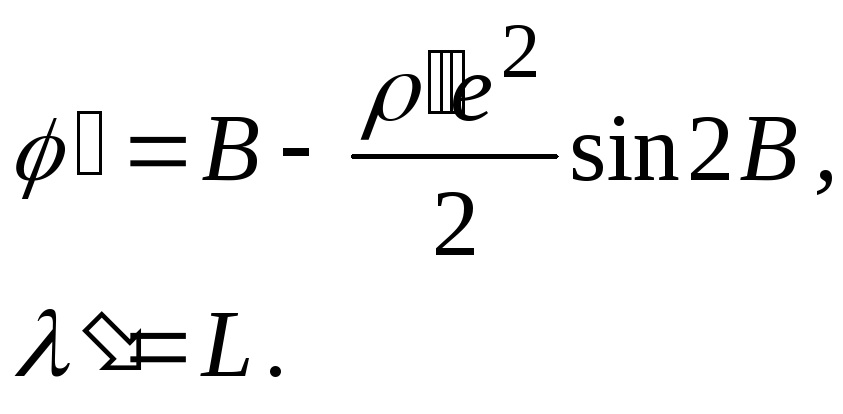(2.20)

7. Если мы хотим, чтобы масштаб по меридиану на шаре был равен масштабу по меридиану на эллипсоиде, сферические координаты определяются из выражений:

(2.21)

где X - вычисляется по формуле (2.9).