6.2 Равнопромежуточные конические проекции

Рассмотрим сначала эту проекцию на шаре. Для равнопромежуточной проекции . Вот почему, приняв главный масштаб , на основании первого выражения (6.2) будем иметь

,

откуда

.

Интегрируя правую и левую части этого равенства, найдём

, (6.9)

где - - расстояние от экватора до параллели с широтой , -постоянная интегрирования. Здесь выражена в радианной мере.

Раскроем геометрический смысл постоянной интегрирования. Если точка находится на экваторе, т.е. , то

,

следовательно, — радиус изображений экватора.

Полюс в равнопромежуточной проекции представляет дугу окружности, которую называют полярной линией. Радиус полярной линии определяется из выражения

.

Масштаб по параллелям, принимая во внимание (6.9) будет равен

. (6.10)

Так как в конической проекции параллели пересекают меридианы под прямым углом, угол равен 90°, и направление осей эллипса искажений совпадают с направлениями меридиана и параллели, т.е. , .

Поэтому на основании (3.12) наибольшему искажению углов соответствуют направления

на глобусе, (6.11)

на карте.

Величина наибольшего искажения углов, исходя из (3.7), определяется из выражения

. (6.12)

Радиус параллели с наименьшим масштабом, принимая во внимание (6.6), равен

(6.13)

Радиус экватора будет соответственно равен

, (6.14)

где - выражено в радианной мере, коэффициент пропорциональности на основании (6.8)

. (6.15)

Таким образом, чтобы рассчитать коническую проекцию, необходимо задать широту параллели касания , где , вычислить по формуле (6.13) радиус этой параллели, найти радиус экватора, а из (6.9) радиусы всех остальных параллелей. Определить по (6.15) коэффициент пропорциональности и вычислить по формуле (4.8) долготы на карте. Величины искажений определятся из выражений (6.10) и (6.12).

Из приведённого выше следует, что в зависимости от выбора широты параллели касания мы можем получить множество равнопромежуточных конических проекций.

Рассмотрим теперь равнопромежуточную коническую проекцию на эллипсоиде.

Так как в равнопромежуточной проекции , радиус параллели касания, где , определяется из второго выражения (6.6)

(6.16)

где и - широта и радиус кривизны первого вертикала на параллели касания соответственно.

Радиус любой другой параллели с широтой будет равен

(6.17)

где - длина дуги меридиана от параллели касания до параллели с широтой , вычисляемая по формуле (2.18)

Коэффициент пропорциональности в соответствии с (6.8) будет равен

(6.18)

а увеличение масштаба по параллели согласно (6.4)

. (6.19)

Максимальное искажение углов определяется по формуле (6.12). В качестве примера рассмотрим расчет равнопромежуточной конической проекции на эллипсоиде для карты Украины в масштабе 1:1000000.

Широту параллели касания, как и в случае цилиндрических проекций примем .

Коэффициент пропорциональности .

Все остальные данные приведены в таблице 6.1

Таблица 6.1

44°	619,821	1,0023	0° 08’
45°	608,713	1,0013	0° 04’
46°	597,598	1,0006	0° 02’
47°	586,482	1,0001	0°
48°	575,364	1,0000	0°
49°	564,244	1,0002	0°
50°	553,122	1,0006	0° 02’
51°	541,998	1,0014	0° 05’
52°	530,872	1,0026	0° 09’

Как видим, искажение расстояний по параллели в этой проекции не превышает для всей территории Украины

2,3 м/км в южных района;

2,6 м/км в северных районах.

Наибольшие искажения углов составляет не более 9 минут, а потому при решении многих картометрических задач могут рассматриваться как пренебрегаемо малые.

Наибольшие искажения площадей составляет:

23 м² /га на юге;

26 м²/га на севере.

Чтобы приведенные в таблице 6.1 искажения сделать ещё меньше имеет смысл вместо проекции на касательный конус использовать проекцию на секущий конус, как это показано на рис.4.8.

В этом случае на первый план выдвигается задача правильного выбора параллелей сечения. Существует несколько способов такого выбора. Рассмотрим один из них.

Если обозначить через и , широты крайних параллелей изображаемой территории, то широты параллелей сечения определятся по формулам

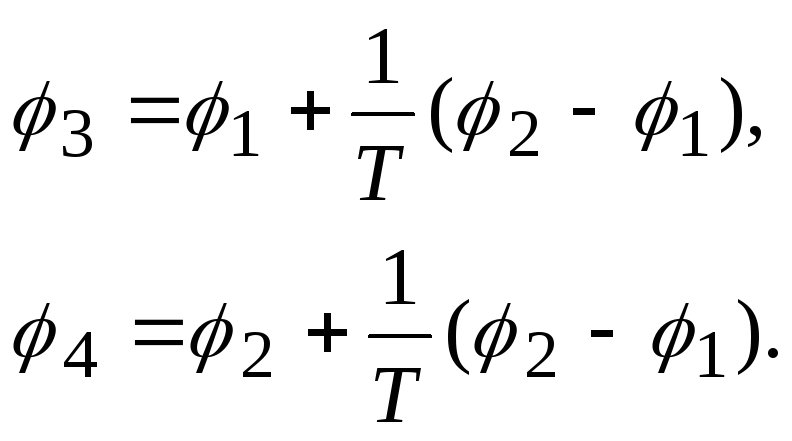(6.20)

где: Т — коэффициент зависящий от конфигурации картографируемой территории, который принимает следующие значения:

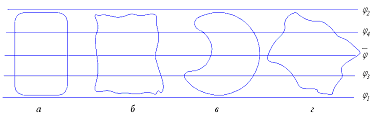
Рис.6.2

1. Если территория имеет небольшое протяжение по широте (рис. 6.2а), .

2.Для территории, имеющей форму прямоугольника или параллелограмма (рис.6.2 б), .

З. Если изображаемая территория имеет форму круга, эллипса или какой-либо другой криволинейной фигуры (рис.6.2в), .

4.Если территория имеет форму, близкую к четырёхугольнику или ромбу (рис.6.2.г), .

Получаемые по формулам (6.20) значения округляют до целого градуса или половины градуса.

Если говорить о территории Украины, то она имеет протяжение по широте 8°, а по долготе 19°. Вот почему для неё наиболее подходящим будет вариант, представленный на рис.7.2а. Тогда на основании (6.20) имеем

,

.

Рассмотрим теперь равнопромежуточную секущую коническую проекцию на эллипсоиде.

Из выражения (6.2) имеем

Обозначив ,

где: - приращение длины дуги меридиана, найдём

Откуда интегрированием левой и правой части получим

(6.21)

где - длина дуги меридиана, вычисляемая по формуле (2.8).

В соответствии с (6.19), имея в виду, что на параллелях сечения , подставляя вместо с его значение из (6.21), можно получить

. (6.22)

Обозначив в (6.22)

(6.23)

где: - радиусы параллелей сечения, решим уравнение относительно и . В результате получим

(6.24)

. (6.25)

Рассчитаем параметры этой проекции для карты Украины в масштабе 1:1000000.

,

,

,

,

,

.

Все остальные данные приведены в таблице 6.2 .

44°	619,821		1,0023		0° 08’
45°	608,713		1,0013		0° 04’
46°	597,598		1,0006		0° 02’
47°	586,482		1,0001		0°
48°	575,364		1,0000		0°
49°	564,244		1,0002		0°
50°	553,122		1,0006		0° 02’
51°	541,998		1,0014		0° 05’
52°	530,872		1,0026		0° 09’

Таблица 6.2

Сравнивая данные, приведённые в таблицах 6.1 и 6.2, мы видим, что проекция на секущий конус позволяет уменьшить искажения длин линий по параллели, площадей и углов почти в два раза.

Наибольшее искажение на параллели составляет 1,4 м/км для расстояний;

14 м²/га для площадей,

0° 05’ для углов.