5.8 Равноугольная поперечно-цилиндрическая проекция на секущем цилиндре (проекция utm)

Чтобы уменьшить искажение на краю шестиградусной зоны, присущие проекции Гаусса-Крюгера, в некоторых странах применяется поперечно-цилиндрическая проекция Меркатора на секущем цилиндре, получившая название проекция UTM.

В этой проекции (рис.5.12) цилиндр пересекает поверхность шара или эллипсоида по линиям малых кругов, параллельных осевому меридиану и отстоящих от него на к западу и востоку.

Расстояние по дуге большого круга от плоскости осевого меридиана P₁AaP до плоскости малого круга проходящей через линию сечения Q₁A₁a₁Q - равному 180 км, соответствует центральный угол aOa₁. Если принять радиус шара R=6367558 для случая, когда длина меридиана на шаре равна длине меридиана на

Рис.5.12

эллипсоиде (см. 2.10), этот угол можно вычислить по формуле

.

Имея угол , для вычисления прямоугольных координат по известным сферическим мы можем воспользоваться выражениями (5.8) и (5.13) заменив в них на , а координаты на и

(5.29)

Так как проекция равноугольная, увеличение по осям и будет

. (5.30)

Увеличение площадей

.

Так как для осевого меридиана , и , то увеличение по осевому меридиану на всём протяжении от экватора до полюса составит

или

что соответствует 40 см на 1 км, а увеличение площадей равно

или

что соответствует - 8 м² на 1 га.

Для территории Украины искажение длин линий на краю шестиградусной зоны составит

южная часть или 31 см на 1 км;

северная часть или 12 см на км.

Искажение площадей соответственно

южная часть или 6 м² на 1 га;

северная часть или 2м² на 1 га.

Сравнивая эти данные с соответствующими показателями для проекции Гаусса-Крюгера, мы видим, что в проекции UTM искажения длин линий и площадей существенно меньше.

6 Конические проекции

6.1 Общая теория конических проекций

Как уже отмечалось в 4.2 в конической проекции меридианы - прямые, расходящиеся лучами из центра проекции в , а параллели -дуги концентрических окружностей с центром в точке .

Уравнение конической проекции в общем виде представлено выражениями

(4.8)

(4.9)

Таким образом при задании конкретного вида проекции необходимо установить значение коэффициента пропорциональности c и вид функции .

Для установления общих закономерностей конических проекций возьмём на глобусе и карте (рис.6.1) по два бесконечно близких

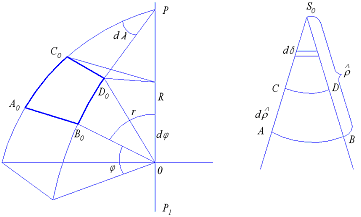
Рис.6.1

меридиана, составляющих между собой угол на глобусе и угол на карте, и по две бесконечно близкие параллели, отстоящие одна от другой на угол на глобусе и на отрезок - на карте. Знак минус взят потому, что с возрастанием широты радиус убывает.

Частный масштаб по меридиану будет равен

- для шара, (6.1)

- для эллипсоида.

Увеличение масштаба m по меридиану для шара и эллипсоида будут соответственно равны

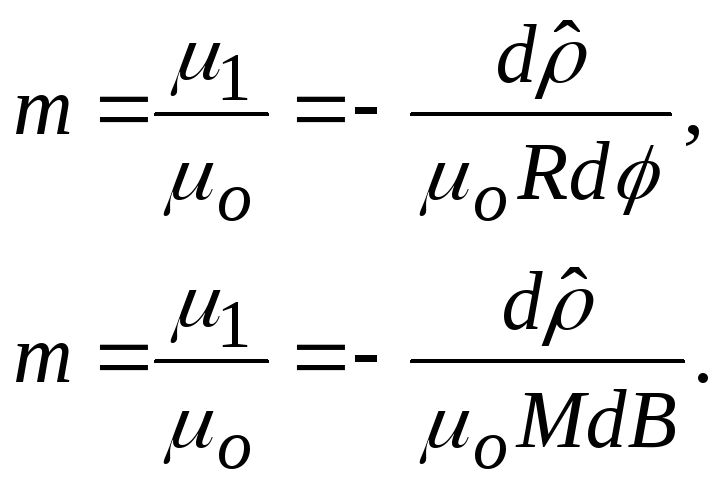(6.2)

где - масштаб глобуса и главный масштаб карты.

Для частного масштаба по параллелям можем записать

. (6.3)

Продифференцируем (4.8) и подставим в (6.3). После очевидных преобразований получаем

для шара, (6.4)

для эллипсоида.

Соответственно увеличение по параллелям для шара и эллипсоида будет

(6.5)

Так как в конической проекции меридианы и параллели перпендикулярны, то главные направления эллипса искажений совпадает с направлением меридиана и параллели.

Масштаб площадей определяется из выражения (3.20)

а направления наибольшего искажения углов из выражения (3.12)

где , , если , или , , если .

Опуская выводы, приведём готовые формулы для определения параметров проекции на широте, где увеличение по параллели наименьшее т.е. .

для шара, (6.6)

для эллипсоида,

где черта над соответствующими обозначениями означает, что они соответствуют минимуму n.

На основании (6.5) можем записать

. (6.7)

Подставим в (6.7) значение из (7.6) и принимая во внимание (6.4), найдём значение коэффициента пропорциональности c

,

откуда

. (6.8)

Таким образом, задавая широту или параллели, где мы хотим иметь наименьшее увеличение можно определить коэффициент пропорциональности c и параметры