5.2 Простая равнопромежуточная цилиндрическая проекция

Предложена в 1438г. португальским принцем Генрихом Мореплавателем.

В этой проекции (рис. 5.2) расстояние между меридианами равно выпрямленной дуге экватора, а расстояние между параллелями - выпрямленной дуге меридиана. Если принять Землю за шар радиусом R, то и определятся из уравнений

Рис. 5.2

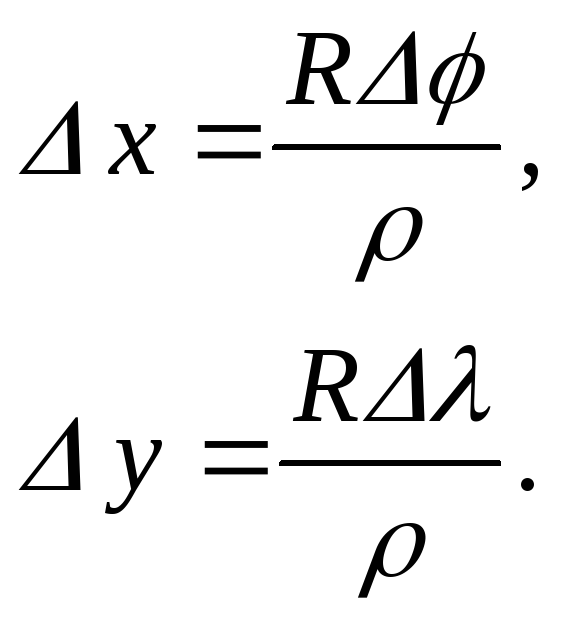(5.7)

Сетка меридианов и параллелей - квадраты. Увеличение по меридиану и параллели будут

Соответственно полуоси эллипса искажений будут равны

Увеличение площадей

.

Наибольшее искажение направлений

.

Эта проекция может быть применена для территорий, расположенных вблизи экватора. В средних широтах, в т.ч. в Украине, эта проекция неприменима из-за больших искажений.

5.3 Прямоугольная равнопромежуточная цилиндрическая проекция

В целях уменьшения искажений вместо касательного по экватору цилиндра берётся секущий цилиндр с параллелями сечения .

Расстояние между меридианами (рис.5.3) равно выпрямленной дуге параллели сечения, а расстояние между параллелями выпрямленной дуге меридиана. Сетка меридианов и параллелей прямоугольная.

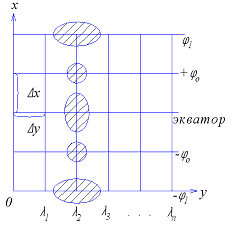
Рис.5.3

Если принять Землю за шар, и определяются по формулам

(5.8)

Увеличение по меридиану и параллели будет

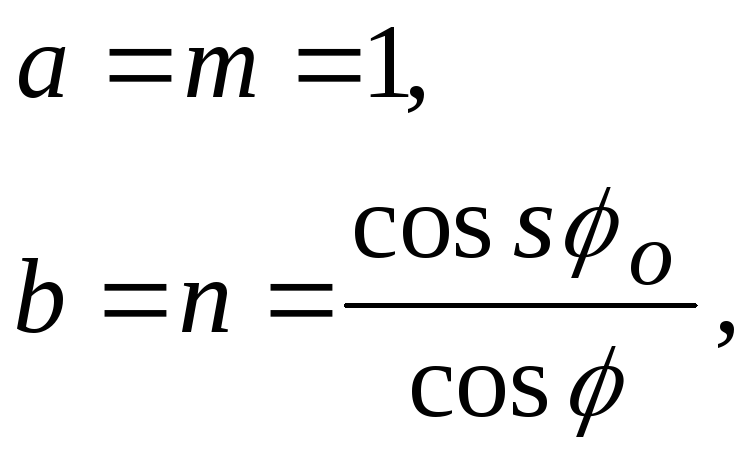
между параллелями сечения , на параллели сечения , вне этого интервала .

Увеличение площадей

.

Максимальное искажение направлений

Для территории Украины самая южная точка Форос в Крыму имеет широту , а самая северная точка пос. Знобь Новгородская в Черниговской области .

Если за параллель сечения принять среднюю параллель, искажения по территории Украины распределятся, как это показано в таблице 5.1

44°	1,000	0,930	4°08'
45°	1,000	0,946	3°09'
46°	1,000	0,963	2°08'
47°	1,000	0,981	1°05'
48°	1,000	1,000	0°
49°	1,000	1,020	–1º08'
50°	1,000	1,041	–2º18'
51°	1,000	1,063	–3º31'
52°	1,000	1,087	–4º46

Таблица 5.1

На основании данных, приведённых в таблице 5.1 можно заключить:

• Наибольшие искажения вдоль параллели и искажение площадей в этой проекции составляют 7% на юге и около 9% на севере

• Искажения углов по краям территории превышают 4°

• Искажения к северу от параллели сечения возрастают быстрее, чем к югу от неё.

5.4 Равноугольная цилиндрическая проекция Меркатора

Предложена в 1569 году фламандским картографом Г. Меркатором.

Рассмотрим сначала эту проекцию для шара.

В рассмотренной нами ранее простой цилиндрической проекции увеличение масштаба по меридиану равно единице, а по параллели . Таким образом кружок, взятый на глобусе, изображается в этой проекции эллипсом, вытянутым по параллели.

Чтобы проекция была равноугольной, как это следует из выражения (3.7), необходимо и достаточно обеспечить равенство

.

Следовательно, чтобы сделать цилиндрическую проекцию равноугольной, нужно меридианы, также как и параллели, вытянуть в раз. Как это осуществить практически? Разделим меридианы, начиная от экватора, на бесконечно малые отрезки , как это оказано на рис.5.4. Середине каждого такого отрезка соответствует своя широта. Тогда длина отрезка меридиана от экватора до некоторой точки с широтой будет равна

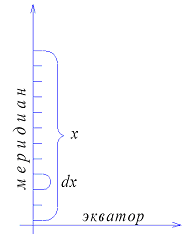
Рис.5.4

. (5.9)

В свою очередь, как это следует из рис.5.1

(5.10)

Подставляя значение из (5.10) в подынтегральное выражение (5.9) и выполнив интегрирование, найдём

. (5.11)

Ордината сохранит своё значение, т.е.

. (5.12)

Сетка меридианов и параллелей прямоугольная (рис.5.5). Увеличение по меридиану и параллели будет

.

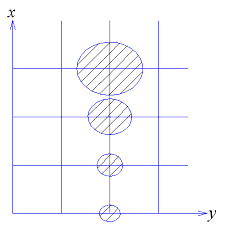
Рис.5.5

Эллипсы искажений представляют собой окружности радиусом .

Если касательной по экватору цилиндр заменить секущим по параллели , то выражение (5.11) принимает вид

, (5.13)

а второе выражение (5.8) остаётся без изменений.

Увеличение по меридиану и параллели

.

Увеличение площадей

.

Для территории Украины, если принять , увеличение площадей составит, как это следует из табл.5.2, до на юге до на севере.

Таблица 5.2

	44°	45°	46°	47°	48°	49°	50°	51°	52°
	0,865	0,895	0,927	0,962	1	1,04	1,084	1,13	1,182

До сих пор мы рассматривали проекцию Меркатора на шаре. Если за модель Земли принять эллипсоид вращения, формулы для вычисления и принимают вид

(5.14)

где - радиус параллели касания или сечения

,

, - первый эксцентриситет земного эллипсоида, определяемый выражением (2.2).