5. Цилиндрические проекции

Рис. 4.5

Опишем вокруг глобуса цилиндр, касательный по экватору (рис.4.5). Продолжим плоскости меридианов и параллелей до пересечения с поверхностью цилиндра. Линии пересечения этих плоскостей примем за изображения меридианов и параллелей. Разрежем цилиндр по образующей и развернем на плоскость. В результате получим картографическую сетку в цилиндрической проекции.

Меридианы и параллели изобразятся в этой проекции взаимно перпендикулярными прямыми.

Общее уравнение цилиндрических проекций:

(4.11)

где - коэффициент пропорциональности.

Из (4.11) следует, что меридианы всегда – равноотстоящие прямые.

Таким образом, различные цилиндрические проекции различаются видом функции , т.е. способом построения параллелей.

Сравнив азимутальные, конические и цилиндрические проекции напрашивается вывод.

Азимутальная проекция – частный случай конической проекции, когда угол при вершине конуса равен , т.е. когда коэффициент пропорциональности (4.8).

С другой стороны, цилиндрическая проекция – также частный случай конической проекции, когда вершина конуса, касательного к глобусу по экватору, удалена в бесконечность, а угол при вершине конуса равен нулю.

Таким образом, в широком смысле конические проекции заключают в себе все цилиндрические и азимутальные проекции, в том числе и перспективные, являющиеся частным случаем азимутальных.

Наряду с нормальными проекциями, представленными на рис. 4.2, 4.3, 4.4, 4.5, азимутальные, конические и цилиндрические проекции могут быть поперечными, когда для азимутальных проекций картинная плоскость касается глобуса на экваторе, а ось цилиндра или конуса лежит в плоскости экватора, как это показано на рис.4.6, и косыми, когда главный луч, ось конуса или цилиндра расположены относительно оси вращения под углом , причем , как это показано на рис.4.7.

Рис.4.6 Рис. 4.7

До сих пор мы рассматривали касательные проекции. Это азимутальные проекции, касающиеся глобуса в точке касания (рис.4.3, 4.7), нормальные конические и цилиндрические проекции, касающиеся глобуса по параллели касания, в т.ч. по экватору (рис. 4.2, 4.5) и поперечно-цилиндрические проекции, касающиеся глобуса по меридиану касания (рис. 4.6).

Однако, перечисленные выше проекции могут быть также секущими проекциями, когда картинная плоскость пересекает глобус по параллели в азимутальной проекции, а конус или цилиндр пересекают глобус по двум параллелям, которые называют параллелями сечения в конической и цилиндрической проекции, как это показано на рис. 4.8.

Рис. 4.8

Кроме перечисленных выше проекций для мелкомасштабного картографирования принимают ещё несколько видов проекций, в т.ч:

6. Поликонические проекции

Поликоническими называются проекции, у которых средний меридиан – прямая линия и сохраняет длину, т.е. m=1, параллели -разноцентренные окружности, ортогональные среднему меридиану, остальные меридианы – кривые линии, ортогональных параллелям и обращенные вогнутостью к среднему меридиану.

Общие уравнения поликонических проекций

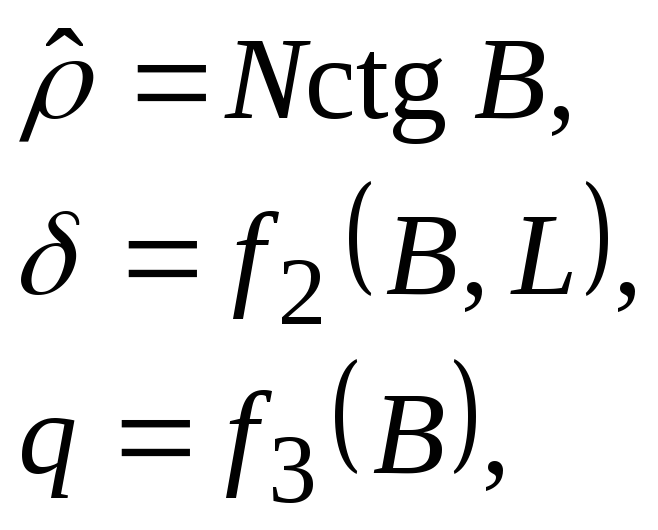(4.12)

где: - радиус параллелей, - угол между меридианами, -координата центров параллелей.

7. Псевдоконические проекции

Псевдоконическими называют проекции, у которых параллели , также, как и у конических проекций ,-концентрические окружности, а меридианы – какие угодно кривые.

Общие уравнения псевдоконических проекций

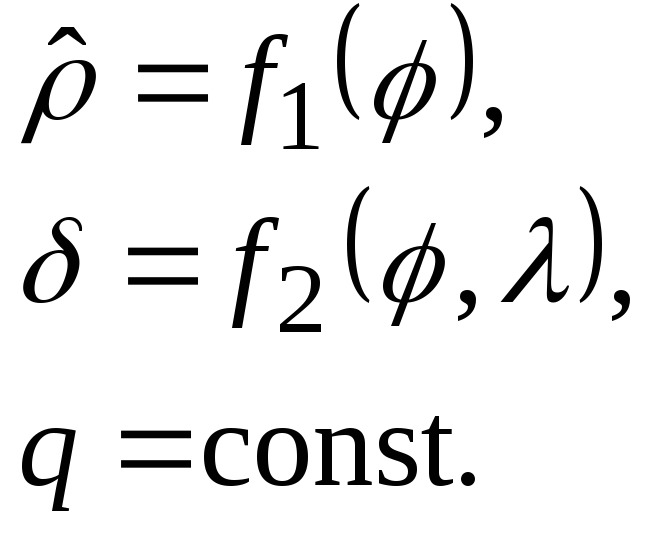(4.13)

8. Псевдоазимутальные проекции

У этих проекций параллели – замкнутые концентрические окружности, меридианы – в виде кривых, симметричных относительно осевого меридиана.

Общие уравнения псевдоазимутальных проекций

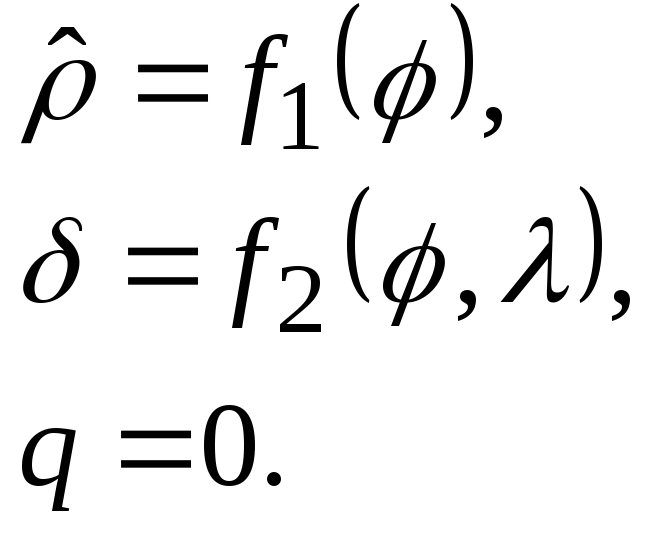(4.14)

9. Псевдоцилиндрические проекции

Псевдоцилиндрические проекции это проекции у которых параллели – параллельные линии, а меридианы – т.н. псевдоцилиндрические кривые.

Общие уравнения псевдоцилиндрических проекций

(4.15)

5 ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ

5.1 Общая теория цилиндрических проекций

Общее уравнение цилиндрических проекций в соответствии с (4.11) будет

где -расстояние параллелей от экватора или от параллели сечения, -расстояние от начального меридиана до данного, -коэффициент пропорциональности.

Найдём выражение для масштабов вдоль меридиана и вдоль параллели, принимая землю за шар (рис.5.1). Полагая бесконечно малыми отрезками, найдём частные масштабы по меридиану и параллели. По определению масштаб вдоль меридиана будет

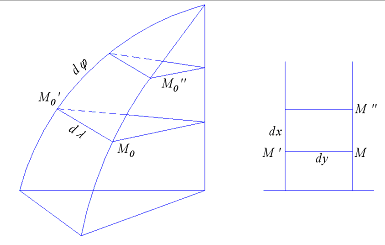
Рис.5.1

, (5.1)

а вдоль параллелей, принимая во внимание (4.11)

, (5.2)

где: r – радиус параллели.

Увеличение масштабов вдоль меридиана и параллели будут соответственно равны

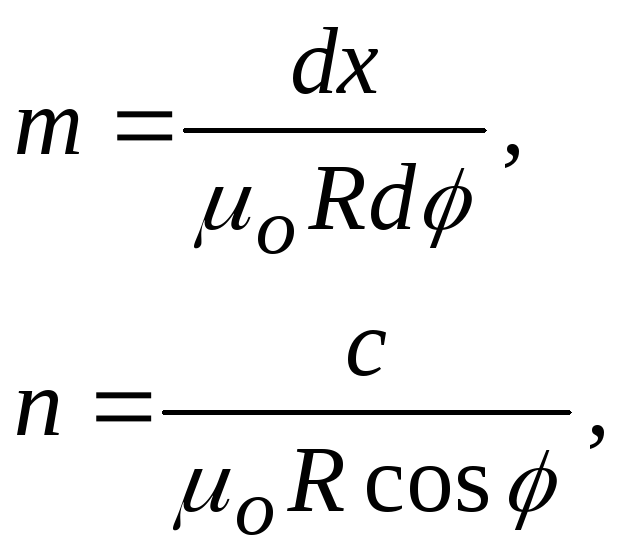(5.3)

где - главный масштаб карты.

Для определения коэффициента пропорциональности задаём широту параллели касания или сечения, где частный масштаб равен главному т.е.

.

Откуда . Подставив во второе уравнение выражений (4.11) и (5.3), найдём

, (5.4)

. (5.5)

Так как меридианы и параллели пересекаются под прямым углом, т.е. , то полуоси эллипса искажений на основании (3.24) будут равны увеличению по меридиану и параллели. Следовательно и .

Если Землю принять за эллипсоид, формулы для увеличения принимают вид

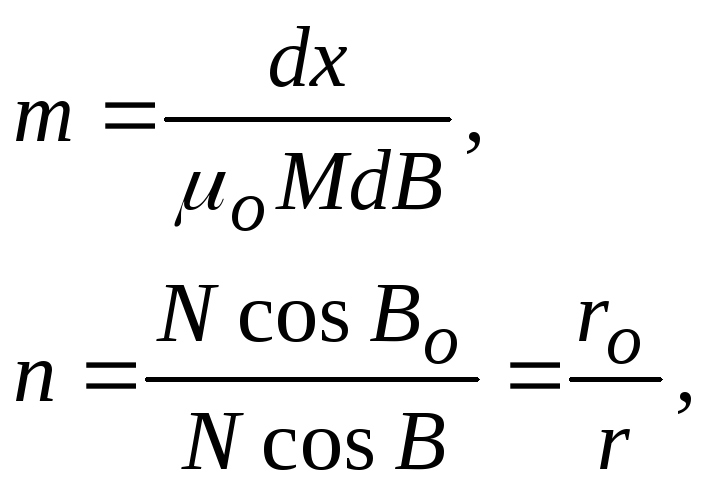(5.6)

где - радиус параллели сечения или касания.

Из (4.11) и (5.5) следует, что для задания цилиндрической проекции необходимо на основании тех или иных дополнительных условий задать в явном виде функцию и коэффициент пропорциональности .