§ 6.9. Теплоемкость и энтальпия влажного воздуха

Изобарную теплоемкость с_p обычно относят к 1 кг сухого воздуха или к (l+d) кг влажного воздуха. Она равна сумме теплоемкостей 1 кг сухого воз­духа и d кг пара

_,

где с_pВ - удельная изобарная теплоемкость сухого воздуха; с_рП - удельная

изобарная теплоемкость водяного пара.

Можно принять с_рВ ≈ 1 кДж/(кг^.К) = const, с_рП = 1,96 кДж/(кг^.К). Тогда

Энтальпия влажного воздуха определяется как энтальпия газовой смеси, состоящей из 1 кг сухого воздуха и d кг водяного пара

где i_В=c_pВ t ≈ t - энтальпия сухого воздуха; - эн­тальпия водяного пара, находящегося во влажном воздухе в перегретом со­стоянии; t - температура влажного воздуха; r - скрытая теплота парообразо­вания; с_рВОД = 4,19 кДж/(кг^.К) - удельная изобарная теплоемкость воды; t_н - температура насыщения при парциальном давлении пара в смеси; t - темпе­ратура влажного воздуха.

Учитывая, что для 0 ≤ t_Н ≤ 100°С кДж/(кг^.К)

, получим

§6.10. id - ДИАГРАММА ВЛАЖНОГО ВОЗДУХА

Параметры влажного воздуха можно определить графически, пользуясь id - диаграммой влажного воздуха, предложенной Л.К.Рамзиным в 1918 г. (рис. 6.10).

На этой диаграмме вертикальные линии - линии влагосодержания d (г/кг); линии, наклоненные к вертикальным линиям под углом 45°, являются линиями постоянных энтальпий. Кроме того, на диаграмме имеются линии постоянных температур влажного воздуха, кривые относительной влажности φ воздуха, кривая парциальных давлений p_П = f (d). Диаграмма обычно строится для какого-либо среднего барометрического давления.

По id - диаграмме, зная температуру t и относительную влажность φ, можно определить энтальпию i, влагосодержание d и парциальное давление Р_П. По температурам сухого и мокрого термометров можно определить температуру точки росы, т.е. температуру, при которой воздух насыщен во­дяным паром (φ = 100%).

Процесс нагрева влажного воздуха на id - диаграмме изображается вер­тикальной прямой линией (линия АВ) при d = const. Процесс охлаждения также протекает при d = const и изображается вертикальной прямой (линия МО). Этот процесс справедлив только до состояния полного насыщения (φ = 100%). При дальнейшем охлаждении воздух будет пересыщен влагой, и она будет выпадать в виде росы.

Процесс конденсации условно можно считать проходящим по линии φ = 100%. Например, при конденсации от точки О до точки S количество об­разовавшейся воды будет равно .

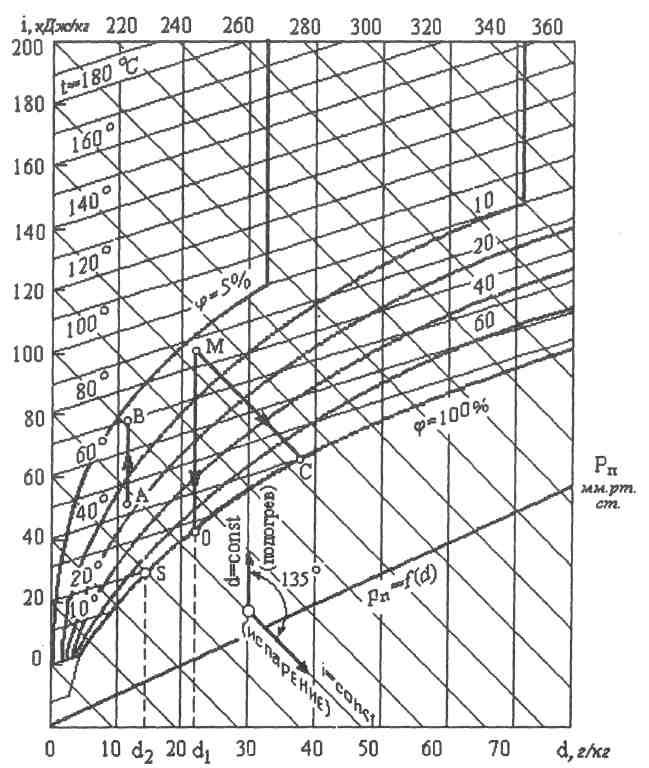
Рис. 6.10

Температура точки росы с помощью id - диаграммы находится следую­щим образом. Из точки, характеризующей данное состояние влажного воз духа, проводится вертикаль до пересечения с линией φ = 100%. Изотерма, проходящая через эту точку пересечения, и будет определять температуру точки росы.

Глава 7 термодинамика газового потока

§ 7.1. Уравнение энергии газового потока

Процессы движения газа, происходящие в различных теплотехнических установках, связаны с преобразованием энергии в газовом потоке. Расчеты рабочих процессов этих установок строятся на общих положениях теории га­зового потока. Эта теория базируется на основных положениях термодина­мики и на ряде допущений, к числу которых относятся следующие:

1.Течение газа установившееся, т.е. в каждом выделенном сечении пара­метры газа во всех его точках остаются постоянными.

2.От сечения к сечению происходят бесконечно малые изменения пара­метров газа по сравнению со значениями самих параметров. Течение газа стационарное.

При таких допущениях газ при движении будет проходить ряд последова­тельных равновесных состояний.

Стационарное течение газа описывается системой уравнений, включаю­щей уравнение неразрывности потока, уравнение состояния и уравнение энергии (уравнение 1-го закона термодинамики применительно к газовому потоку).

Уравнение неразрывности характеризует неизменность массового расхо­да газа в любом сечении канала при установившемся течении. Это уравнение имеет вид

,

или

,

где G - массовый секундный расход газа; , F₂ - площади поперечных сече­ний канала; w₁ , w₂ - скорости в соответствующих сечениях; ρ₁,ρ₂- плотности газа для тех же сечений потока (ρ=l/v).

Для одномерного газового потока в соответствии со вторым законом Ньютона (сила равна массе, умноженной на ускорение) можно записать сле­дующее соотношение [11]

где

- изменение давления по координате х;

- изменение скорости по координате х;

- сила, действующая на выделенный элементарный объем dV;

- ускорение элементарной массы газа pdV.

Последнее соотношение можно переписать в виде

.

Учитывая, что ρ=1/v, получим

_(7.1)

Полученное соотношение показывает, что приращения давления dp и ско­рости dw имеют разные знаки. Следовательно, скорость одномерного потока возрастает с уменьшением давления.

Величина -vdp совпадает с формулой для располагаемой работы dl в уравнении первого закона термодинамики вида

.

Отсюда уравнение первого закона термодинамики для газового потока при отсутствии сил тяжести и сил трения в газе примет вид

, (7.2)

где приращение кинетической энергии газа на выделенном участке.

Так как , то

, (7.3)

где d(p v) = pdv+ vdp - элементарная работа проталкивания.

Последнее уравнение показывает, что теплота, сообщаемая газу, затрачи­вается на изменение внутренней энергии, на работу проталкивания и на из­менение внешней кинетической энергии газа.

Уравнения (7.2),(7.3) являются основными для потоков газа и пара, при­чем они справедливы как для обратимых (не сопровождающихся действием сил трения), так и для необратимых течений (при наличии сил трения). При наличии сил трения должна затрачиваться работа трения l_тр, которая полностью переходит в теплоту q_тр. Вследствие равенства l_тр =q_тр обе эти величи­ны, имеющие противоположные знаки, взаимно сокращаются.

Уравнение (7.3) с учетом гравитационных сил принимает вид

где gdz - элементарная работа против сил тяжести. Этой составляющей в га­зах ввиду ее малости обычно пренебрегают.

При адиабатном течении газа (dq=0) уравнение (7.2) принимает вид

(7.4)

После интегрирования получим

(7.5)

Таким образом, при адиабатном течении газа сумма удельных энтальпии и кинетической энергии остается неизменной.

Отметим, что уравнения (7.2), (7.3), (7.4) справедливы в случае, когда газ при своем движении совершает лишь работу расширения и не производит полезной технической работы (например, работа на лопатках турбины и проч.). При совершении технической работы уравнение первого закона тер­модинамики (7.3) для потока газа примет вид

, (7.6)

где dl_тех - элементарная техническая работа.

Сравнивая уравнение (7.5) с уравнением первого закона термодинамики (2.17) для расширяющегося, но не перемещающегося газа, получим

.

Таким образом, техническая работа равна работе расширения газа за вы­четом работы проталкивания и работы, затрачиваемой на приращение кине­тической энергии газа.