3.7. Непрямий метод найменших квадратів для системи з n регресій

Розглянемо повну економетричну модель. Система регресій називається повною, якщо:

1. вона має стільки регресій, скільки в ній ендогенних величин;

2. вона має всі змінні, які мають суттєвий вплив на сумісно залежні ендогенні величини;

3. визначник матриці, складеної з коефіцієнтів при ендогенних величинах системи регресій у структурній формі, відмінний від нуля, тобто систему можна розв’язати відносно ендогенних величин.

Нехай повна система регресій структурної форми має n ендогеннних величин та m екзогенних величин

(3.12)

Для оцінки параметрів наведеної системи регресій можна застосувати НМНК, якщо вона ідентифікована.

Економетрична модель буде ідентифікованою, якщо буде ідентифікованою кожна регресія розглянутої системи регресій. Якщо i-та регресія складається з ендогенних величин і екзогенних величин, то ця регресія ідентифікована за умови

або

Припустимо, система ідентифікована. Для оцінювання параметрів цієї системи регресій можна застосувати непрямий метод найменших квадратів. Запишемо систему регресій у матричній формі. Нехай

Тоді система регресій (3.12) запишеться у вигляді:

(3.13)

Якщо визначник , то систему регресій можна розв’язати відносно ендогенних величин, тобто привести до прогнозної форми:

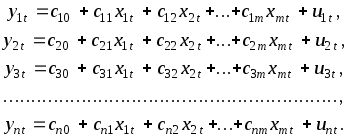(3.14)

Для оцінки параметрів структурної системи регресій (3.14) для кожної з системи регресій застосовується МНК. Сумісна симплекс-таблиця системи нормальних рівнянь матиме вигляд:

0...0......0...0......0...0....................................0...0......1 (3.15) 1 ... 1
... Якщо вибрати діагональні елементі за розв’язувальні елементи, то після кроків ЗЖВ отримаємо розв’язок. ... ... ... ...

Наведена сумісна симплекс-таблиця системи нормальних рівнянь (3.15) дозволяє розв’язати одним циклом ( кроків) ЗЖВ усі системи нормальних рівнянь. Після оцінювання параметрів наведеної прогнозної форми (3.14) визначаються оцінки параметрів структурної системи регресій (3.12). Для цього розглянемо матричну форму системи регресій (3.13). Помножимо цю систему зліва на матрицю :

Якщо позначити , отримаємо прогнозну форму систем регресій .

У матричному рівнянні відомі оцінки параметрів матриці і невідомі оцінки параметрів матриць і . Якщо система регресій ідентифікована, то параметри матриць і однозначно визначаються через параметри матриці із системи рівнянь:

Якщо система ідентифікована, то на частину параметрів матриць і накладені обмеження.

3.8. Двокроковий метод найменших квадратів

У тих випадках, коли система одночасних регресій не ідентифікована, розроблені методи оцінювання параметрів, які враховують багатосторонні зв’язки залежних величин.

Один з таких методів є двокроковий метод найменших квадратів (ДМНК), який є аналогією оцінювання параметрів рекурсивної моделі.

Розглядаємо структурну систему регресій:

(3.16)

На основі статистичних даних потрібно оцінити параметри не ідентифікованої структурної системи регресій.

Для зручності викладання запишемо систему (3.16) у матричній формі: . Позначення матриць і векторів співпадає з позначеннями в попередньому параграфі.

Припустимо, що , тоді систему можна подати в наведеній формі

, або ,

де

Матрицю можна записати в розгорнутому вигляді