2.1 Метод найменших квадратів

Найпоширенішим методом під час розв’язання подібних задач є метод найменших квадратів. Основоположниками методу найменших квадратів є К.Гаусс і П.Лаплас.

Зв’язок між показником Y і фактором X з урахуванням можливих відхилень залишемо у вигляді Y=aX++l, де а і  – невідомі параметри рівняння, l – випадкова зміна. Таким чином, показник Y зображується у вигляді систематичної складової аX+ і випадкової величини l. Залежність =аX+, яка характеризує середнє значення показника Y для даного значення фактора X, називається регресією. Можемо сказати інакше. Регресія характеризує тенденцію зміни показника, зумовлену впливом зміни фактора. Залежність Y=aX++l характеризує індивідуальне значення показника Y з урахуванням можливих відхилень від середніх значень.

Справжні значення параметрів обчислити не можна, оскільки ми маємо обмежене число спостережень, тому отримані розрахункові значення параметрів а і  є статистичними оцінками справжніх параметрів а і . Позначимо оцінки параметрів відповідно через а і b. Тоді рівняння парної регресії буде оцінкою моделі Y=аX+ + l.

Метод найменших квадратів для парної лінійної регресії полягає в підборі таких оцінок параметрів регресії а і b, для яких сума квадратів відхилень спостережуваних значень показника від згладжувальних буде мінімальною. Сума квадратів відхилень має вигляд

(2.1)

Оцінки параметрів а і b лінії регресії Y=аX+b мають бути підібрані методом найменших квадратів так, щоб функціонал Q(a,b) був мінімальним, тобто

(2.2)

Необхідною умовою існування мінімуму функціонала Q(a,b) є рівність нулю частинних похідних цьому функціонала за а і b:

Розкриємо дужки і отримаємо нормальну форму рівнянь:

(2.3)

Розглянемо розв’язок системи нормальних рівнянь. Параметр а визначається такою формулою:

(2.4)

Після ділення чисельника і знаменника на n² отримаємо:

, (2.5)

тобто параметр а дорівнює відношенню кореляційного моменту К(X, Y) до дисперсії фактора X D(X).

У формулі для параметра b поділимо почленно вирази:

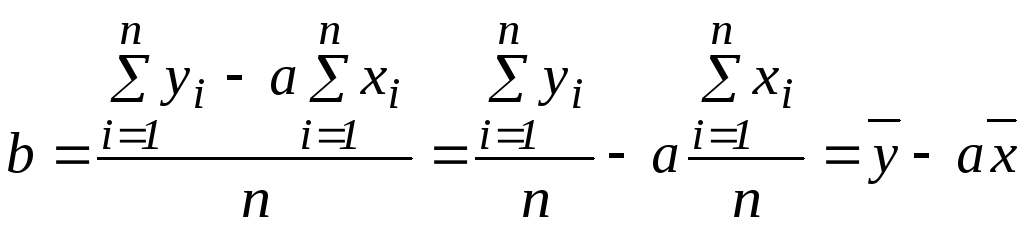(2.6)

Звідси випливає, що лінія регресії проходить через точку, координати якої є середніми значеннями показника Y і фактора X.

Використовуючи рівняння прямої із заданим кутовим коефіцієнтом, яка проходить через точку (x,y), запишемо парну лінійну регресію у вигляді:

(2.7)

У даному випадку парна лінійна регресія виражається через такі числові характеристики: середні значення показника і фактора, кореляційний момент і дисперсію фактора.

Вище, під час визначення оцінок коефіцієнтів лінії регресії, введено статистичний кореляційний момент

(2.8)

Кореляційний момент – це статистична характеристика системи випадкових величин, яка описує не лише зв’язок між випадковими величинами X і Y, а й їх розсіяння.