Правила дифференцирования.

Для того, чтобы уметь вычислять любые производные, необходимо помнить производные основных элементарных функций и знать правила дифференцирования. В таблице представлены основные элементарные функции и их производные.

Основные правила дифференцирования.

1. Производная линейной комбинации функций

(с₁f₁(x)+c₂f₂(x)) = с₁f₁(x)+c₂f₂(x)

Например: (6 sin x - 2 ln x) = 6 cos x -

2. Производная произведения функций

(f(x)g(x)) = f (x) ּg(x) + f(x) ּg (x)

Например: (lnxּcosx)' = ּcosx - lnxּsinx.

3. Производная частного двух функций

Например:

Таблица производных основных элементарных функций

Функция f(x)	Производная f’(x)	Функция f (x)	Производная f’(x)
c (const)	0	ln x
xa (а-любое число)	a x a-1	logax
		ax	ax ln a
		ex	ex
cos x	-sin x	arctg x
sin x	cos x	arcsin x
tg(x)		ctg(x)

Дифференциалом df(x) функции f(x) в точке х называется произведение производной от функции f(x) в этой точке на величину приращения аргумента x

df(x) = . (11)

По определению для независимой переменной Δх = dx. Действительно, если взять функцию f(x) = х, то ее дифференциал dx = df(x) = = (x) x = 1x = x, т.е. dx = х. Поэтому дифференциал функции f(x) записывают чаще так

(12)

Геометрический смысл дифференциала поясняет рис.4. Производная f(x) численно равна тангенсу угла наклона касательной к графику функции f(x). Дифференциал равен изменению ординаты, вызванному изменением аргумента, если двигаться не по графику функции, а по касательной к нему в точке М.

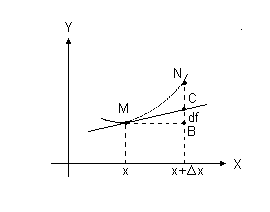
Рис.4. Геометрический смысл дифференциала.

Замена истинного приращения функции f(x) = f(x + x) - f(x) на дифференциал равносильна замене части графика функции на соответствующую часть касательной к этому графику. В этой связи говорят, что дифференциал определяет главную линейную часть приращения функции.

3. Фрактальная графика

Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов, дробный, ломанный». Фракталами называются геометрические объекты — линии, поверхности, пространственные тела, имеющие сильно изрезанную форму и обладающие свойством самоподобия. Самоподобие означает, что фрактал более не менее единообразно устроен в широком диапазоне масштабов. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга

Примерами фракталов в природе являются деревья, например ель, снежинки, кровеносная система человека, береговая линия и т. д. (рис. 5, 6).

Как следует из определения, отдельные элементы фрактала наследуют свойства родительских структур. Поскольку более детальное описание элементов меньшего масштаба происходит по простому алгоритму, описать такой объект можно всего лишь несколькими математическими уравнениями. Фракталы позволяют описывать целые классы изображений, с другой стороны, к изображениям вне этих классов, фракталы применимы слабо.

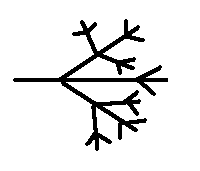
Рис. 5. Простейший фрактал. Рис. 6. Фрактал Ковер Серпинского.

Способность фрактальной графики моделировать образы живой природы вычислительным путем часто используют для автоматической генерации необычных иллюстраций.

Различают геометрические и алгебраические фракталы. Геометрические фракталы самые наглядные. В двухмерном случае их получают с помощью ломаной, называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате многократного повторения этой процедуры, получается геометрический фрактал. Примерами геометрических фракталов могут служит кривые Серпинского (рис 7), треугольник Серпинского (рис 8), дракон Хартера-Хейтуэя (рис. 9).

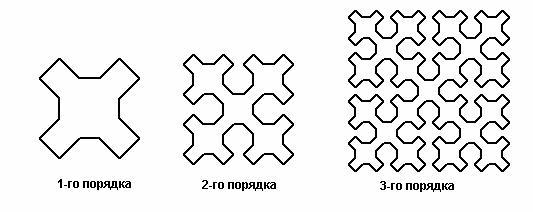
Рисунок 7. Кривые Серпинского

Рисунок 8. Треугольник Серпинского

Рис. 9. 5 итераций при построении фрактала «дракон Хартера-Хейтуэя».

Для фракталов вводится понятие размерности. Для обычных геометрических объектов фрактальная размерность дает привычные числа: 0 для конечного множества точек, 1 для прямой. 2 для плоскости и 3 для пространства. Пусть на некотором этапе развития фрактала пришлось использовать N₁ элементов длины l₁ , а на другом этапе N₂ элементов длины l₂ , тогда фрактальная размерность D определяется по формуле

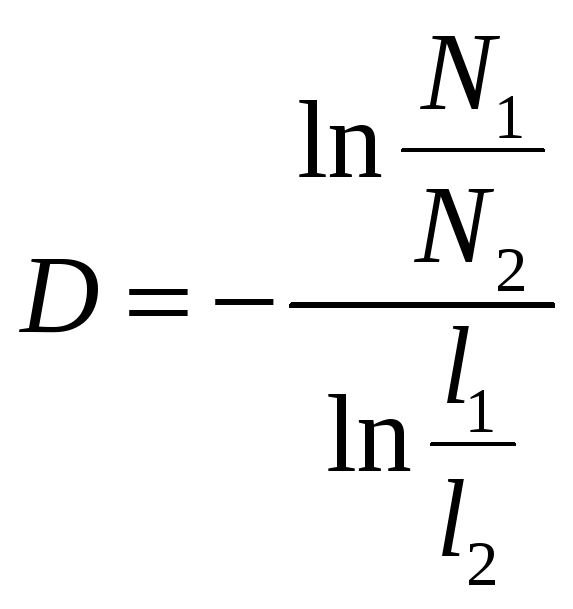(13)

Определим фрактальную размерность ломанной линии, образующей дракона. Один исходный отрезок имеет длину единицу, на третьей итерации имеем 4 отрезка длиной1/2. Следовательно N₁/N₂ = ¼, а l₁/l₂ = 1/(0.5) = 2. D = - ( ln(1/4))/ln(2) = 2. Дракон при бесконечном числе итераций полностью займет кусок плоскости.

На рис. 10 представлен Н — фрактал, образованны буквой Н, на рис.11 фрактал дерево Архимеда. У Н - фрактала при каждой итерации длина отрезка уменьшается вдвое. На рис. 10 и 11 представлены 4 итерации обеих фракталов.

С другой стороны фрактал является функцией – математическим выражением, описывающим эту структуру. Таким образом, получение нового фрактала неразрывно связано с получением соответствующего математического выражения или системы математических выражений. Для построения целого ряд фракталов используются последовательности функций от комплексных чисел. Наиболее известен фрактал «множество Мандельброта» .

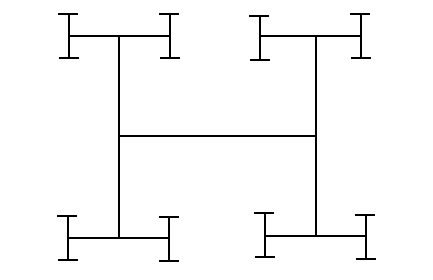
Рис. 10. Н — фрактал.

Рис. 11. Фрактал «дерево Архимеда».

Построение множества Мандельброта (рис. 12)

Рассмотрим последовательность комплексных чисел z_n и возьмем произвольное комлексное число c. теперь для каждого комлексного k рассмотрим последовательность вида

(14)

Множество {k} таких, что данная последовательность стремится к нулю, называется множеством Жюлиа. Объединение всех связных множеств Жюлиа есть множество Мандельброта. Фракталы можно получить, строя множество Мандельброта и выбирая любой способ раскраски.

Рис. 12. Фрактал множество Мандельброта.

Далее приведены другие геометрические и алгебраические фракталы (рис. 13).

Рис. 13. Фракталы.

Литература.

а) Основная учебная литература

1. Ильин В. А., Поздняк Э. Г. Аналитическая геометрия. – М.: Высшая школа, 2004. – 224 с.

2. Ефимов Н. В. Краткий куря аналитической геометрии. – М.: Высшая школа, 2005. – 176 с.

3. Погорелов А.В. Аналитическая геометрия. – М.: ANALITICHESKA, 2005 г.), - 176 с.

б) дополнительная литература и другие информационные источники

4. Шнейдер В.Е. и др. Краткий курс высшей математики, т.1, т. 2.. – М.: Высшая школа, 1978. – 472 с.

5. Кокстер Г. С. К. Введение в геометрию. - М.: Наука, 1966. – 428 с.

6. Колмогоров А.Н. Паркеты из правильных многоугольников.// Квант, №3, 1970.

Вопросы к зачету.

1. Как строится Декартова система координат на плоскости.

2. Какие базовые преобразования системы координат на плоскости существуют.

3. Прямая на плоскости.

4. Базовые кривые второго порядка.

5. Дать определение оси симметрии и плоскости симметрии. Привести примеры.

6. Виды узоров на полосе.

7. Правильные многоугольники, виды, области применения.

8. Золотое сечение, золотой прямоугольник, золотая спираль.

9. Паркеты на плоскости из правильных многоугольников.

10. Паркеты из неправильных многоугольников.

11. Способы построения паркетов.

12. Мозаики Пенроуза.

13. Исскуство Эшера.

14. Предел последоватедьности.

15. Прелел функции. Правили вычисления пределов.

16. Производная функции. Дифференциал. Правила вычисления.

17. Понятие фрактала.

Контрольная работа.

1. Нарисовать примеры 4-х узоров на полосе (свои варианты).

2. Нарисовать паркеты из правильных многоугольников (3,3,3,4,4) - четыре варианта.

3. Нарисовать 10/1, 10/2, 10/3, 10/4 многоугольники.

4. Нарисовать 6 итераций Н – фрактала.

5. Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС. Сделать чертеж.

№	А	В	С
5.1.	(-5, 3)	(10,6)	(1, 5)
5.2.	(-7, 1)	(5, 0)	(2, 5)
5.3.	(5, 1)	(0, 3)	(-2, 4)
5.4.	(5, 2)	(-1, 0)	(4, 4)
5.5.	(2, -2)	(3, -4)	(2, -1)
5.6.
5.7.
5.8.	(-2, 1)	(3, 1)	(0, -2)
5.9.	(-3, 3)	(7, 5)	(4, 8)
5.10	(2, 0)	(5, -2)	(10, 2)

6. Указать тип кривой второго порядка, сделать чертеж.

6.1. .

7. Вычислить пределы

7.6.

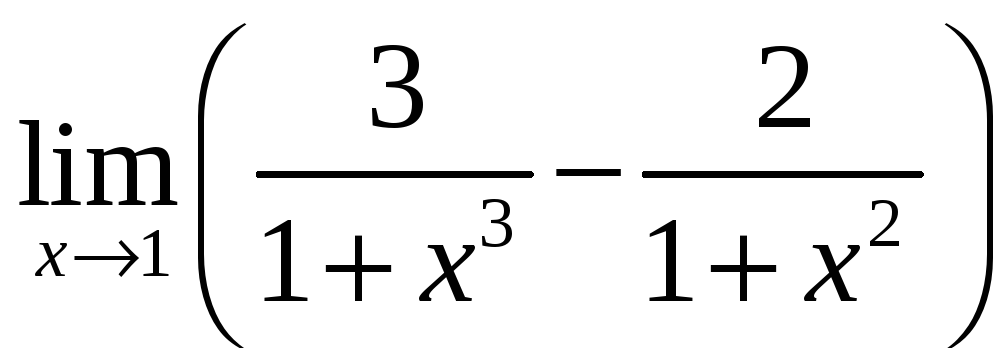
7.9.

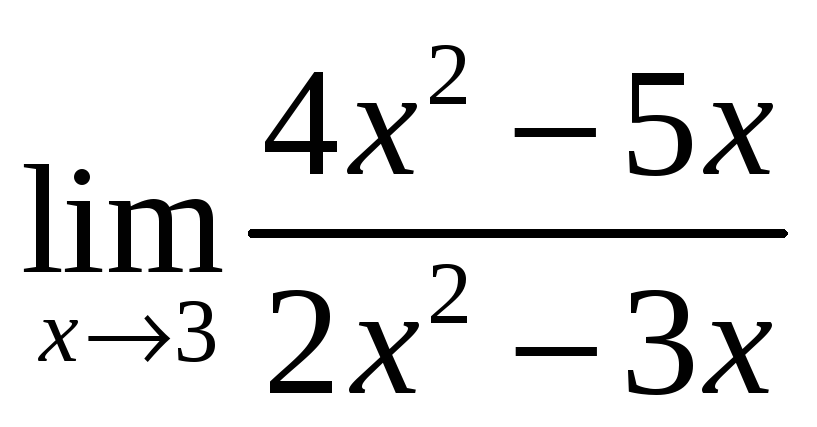
7.10.

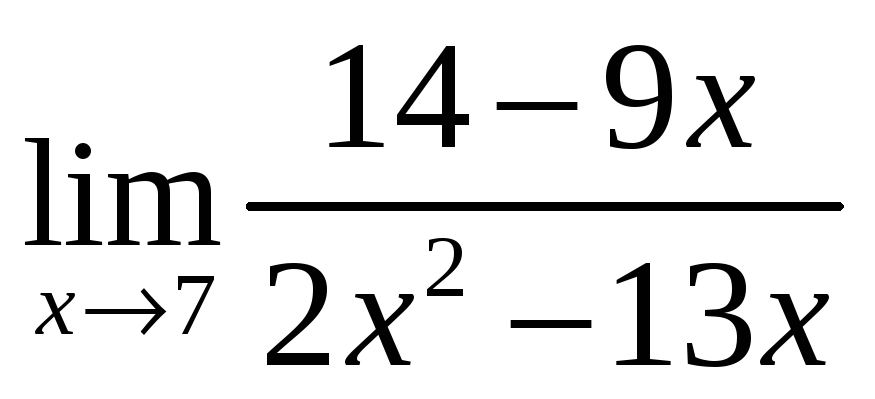
7. Вычислить производную

8.1		8.6
8.2		8.7
8.3		8.8
8.4		8.9
8.5		8.10

44