1.7. Исскуство Эшера.

Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные работы, в которых использованы или показаны широкий круг математических идей. Эшер интересовался всеми видами мозаик - регулярными и нерегулярными (нерегулярные мозаики образуют неповоряющиеся узоры) - а также ввел собственный вид, который назвал "метаморфозами", где фигуры изменяются и взаимодействуют друг с другом, а иногда изменяют и саму плоскость.

Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражением, смещением (переносом) и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шестинаправленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей (рис. 41 а, б).

Регулярное разбиение 

плоскости птицами Рептилии Цикл Эволюция

Рис. 41 а. Метаморфозы Эшера.

Рис. 41 б. Мозаики М. Эшера.

Те же геометрические идеи Эшер использовал, создавая узоры в круге (рис. 42).

Рис. 42. Узоры М. Эшера в круге.

2. Базовые понятия математического анализа.

2.1. Предел числовой последовательности

Числовую функцию, а_n= f(n), заданную на множестве натуральных чисел, называют числовой последовательностью. Говорят, что последовательность задана, если каждому натуральному числу n по некоторому закону f поставлено в соответствие число f(n). В том случае, когда закон f задан формулой, говорят об аналитическом задании последовательности, при этом, как правило, записывают аналитическое выражение для члена а_n. называемого общим членом последовательности. Например, последовательность квадратов целых чисел

1, 4, 9, 16, 25, .., n², ...  {n²}

Часто закон, по которому задается последовательность, позволяет построить очередной член последовательности по известным предыдущим. Такой способ задания называется рекуррентным. Хорошо известная арифметическая последовательность (арифметическая прогрессия)

а, a + d, a + 2d, a + 3d, ..., a + nd, ...,

может быть задана при помощи рекуррентного соотношения

a_n= a_n-1+ d.

Геометрическая последовательность (геометрическая прогрессия)

с, cq, cq², cq³, ..., cqⁿ, ...

может быть задана при помощи следующего рекуррентного соотношения

b_n = qb_n-1 .

Для полного задания последовательности, кроме рекуррентного соотношения, необходимо задать некоторое число первых членов последовательности. Так для арифметической и геометрической последовательностей, из бесконечного числа членов достаточно задать лишь их первые члены а и с (а также и параметры прогрессий d и c.

Рассмотрим три последовательности:

1, 0, -1, -2, -3, ...,-n,... (1)

2, 4, 6, ..., n²,... (2)

1, , , ..., , ... (3)

При увеличении числа n члены первой последовательности неограниченно убывают, члены второй - неограниченно возрастают, а члены третьей последовательности убывают начиная с числа 1 до числа 0. Следовательно, числовые последовательности могут быть ограничены либо сверху, либо снизу, либо и сверху и снизу.

Последовательность называется ограниченной сверху, если существует число M (верхняя граница), такое, что, а_n  M для всех n. Последовательность (1) ограничена сверху, например, числом 2. Поскольку для всех n кроме того выполняется условие а_n  а_n-1, то это убывающая последовательность.

Последовательность (а_n) называется ограниченной снизу, если существует такое число m (нижняя граница), что а_n  m для всех n. Если для всех членов последовательности выполняется условие а_n  a _n-1, то она называется возрастающей. Последовательность (2) является ограниченной снизу возрастающей последовательностью.

Последовательность (а_n) называется ограниченной, если она ограничена и сверху и снизу. Очевидно, что (3) - ограниченная убывающая последовательность.

Рассмотрим последовательность

, ... = {a_n} (4)

Члены этой последовательности по мере возрастания номера члена приближаются к числу 1. Говорят, что последовательность (4) сходится к числу 1.

Формально сходимость последовательности определяется следующим образом. Последовательность {а_n} сходится к числу A, если для любого сколь угодно малого числа  > 0 можно указать такое натуральное число n₀(), что для всех n больших n₀, то есть для n > n₀, выполняется неравенствоa_n - A < .

Проиллюстрируем это определение на примере последовательности (4). Построим отклонение общего члена последовательности от 1.

С возрастанием n это отклонение, уменьшаясь, стремится к нулю. Пусть  =3/500. Вычислим отклонение для а₁₆₆

Тем начиная n = 166 (n₀ =165) выполняется неравенство a_n - 1 < 3/500.

Г

Рис. 1. Геометрическийсмысл

сходимости последовательности

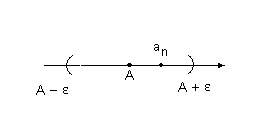еометрический смысл сходимости последовательности проиллюстрирован на рис. 1. Каждому члену числовой последовательности (поскольку это число) соответствует точка на числовой оси. Если последовательность имеет пределом точку A, то для всех номеров последовательности, начиная с некоторого n₀ члены последовательности находятся внутри отрезка (A-,A+), называемого -окрестностью числа A.

Если  очень мало, то число n₀ может быть весьма большим. Следовательно, много членов последовательности окажутся вне -окрестности, однако их всегда будет лишь конечное число. Все остальные члены последовательности, начиная с номера n₀ и более, попадают в -окрестность. Таким образом, если последовательность сходится к A, то какую бы окрестность точки A ни взять, почти все числа а_n попадают в выбранную окрестность.

Отсюда следует, что добавление или исключение конечного числа членов такой последовательности не влияет на ее сходимость. Если последовательность {а_n} сходится к A, то пишут

(5)

(читается “предел а_n при n стремящимся к бесконечности равен A”). В этом случае говорят, что число A есть предел последовательности (a_n) или иначе, при неограниченном увеличении номера общий член последовательности стремится к величине A.

Если последовательность не имеет конечного предела или не имеет предела вообще, то ее называют расходящейся. Так последовательность

-1, 1, -1, 1, ... (-1)ⁿ, ...

расходится, так как в этом случае не существует.

Последовательность (2) тоже является расходящейся, так как по мере возрастания n члены последовательности становятся больше любого наперед заданного числа, то есть а_n стремится к бесконечности В этом случае пишут: . Заметим, что хотя здесь предел формально и существует, но он не является конечным числом.