1.5. Узоры на плоскости. Паркеты.

Паркет (сетка, мозаика или кристалл) - бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Существует три вида правильных многоугольников, полностью заполняющих плоскость треугольник, квадрат и шестиугольник (рис. 32 а, б, в, г, д).

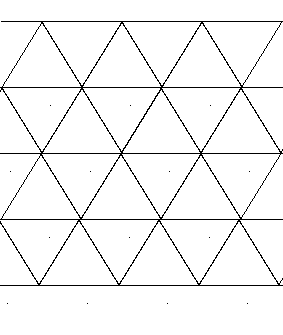
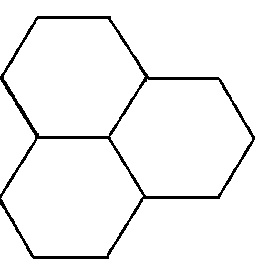
Рис. 32 а, б, в. Правильные многоугольники полностью покрывающие плоскость.

Рис. 32 г. Пол в аббатстве Сен-Мишель, Франция.

Рис. 32 д. Пол в королевском замке Блуа, Франция. Х11 - XV111 в.

Плоскость можно покрыть прямоугольниками. Существует всего 6 вариантов регулярного покрытия плоскости прямоугольниками. Каждый вариант обладает своим набором осей и плоскостей симметрии. Эти узоры мы можем видеть в паркетных полах, кирпичной кладке и мощении тротуаров плиткой. На рис. 23 - 26 показаны все 6 видов узоров и покрытия полов и тротуаров..

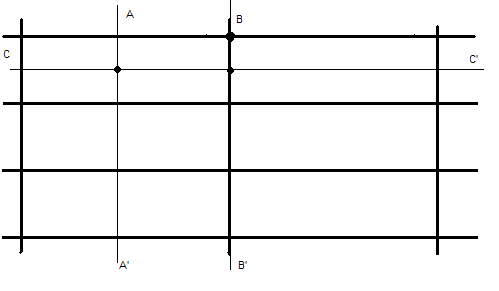
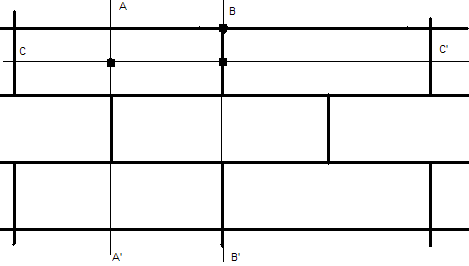
Рис. 23 а, б. Три плоскости симметрии и три оси симметрии.

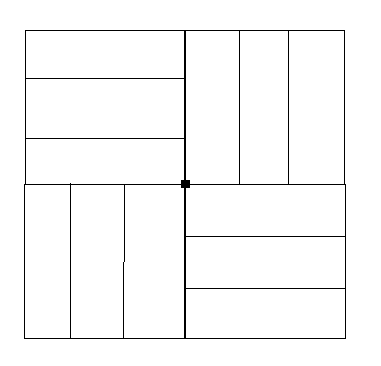
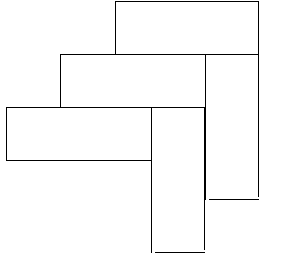
Рис. 24. Одна ось симметрии 4-го порядка. Рис. 25. Нет осей или плоскостей

симметрии.

а б

Рис. 26. Сдвиг по полосе на 1/3 длины. а – три оси симметрии, б – две оси и плоскость.

Рис. 27. Тротуар в Амстердаме (см. рис. 25).

Если использовать другие правильные многоугольники, то известны комбинации разных правильных многоугольников, также образующих паркеты. Будем обозначать многоугольники цифрами по числу их вершин: 3 - правильный треугольник, 4 - квадрат, 6 - правильный шестиугольник, 12 - правильный двенадцатиугольник. Тогда можно показать, что существуют следующие способы уложить паркет комбинациями правильных многоугольников: (3,3,3,3,3,3) (рис. 21 а); (4,4,4) (рис. 21 б); (6,6,6) (рис. 21 в); (4,8,8) (рис. 28 а), (3,3,6,6) - два варианта паркета (рис. 28 б); (4,6,12) (рис. 28 в); (3,4,4,6) - четыре варианта (рис. 28 г); (3,3,3,4,4) - четыре варианта; (3,3,3,3,6); (3,12,12); (цифры в скобках - обозначения многоугольников, сходящихся в каждой вершине.

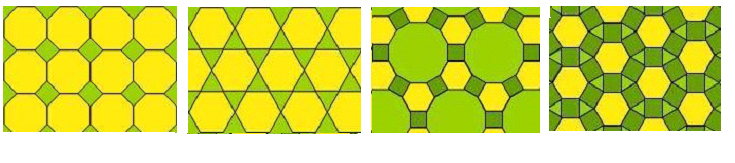
а б в г

Рис. 28. Варианты паркетов.

Можно доказать, что не существует других вариантов укладки паркета из правильных многоугольников (при условии, что любые два многоугольника в паркете имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек).

Паркеты из неправильных многоугольников

Если многоугольники образуют полосу, то ими легко покрыть плоскость (рис. 29)

Рис. 29. Узоры на полосе, образующие паркет.

Плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами. До сих пор не найдены все типы выпуклых пятиугольников, из которых складываются паркеты. Зато доказана теорема, утверждающая: «Нельзя сложить паркет из копий выпуклого семиугольника». В то же время существуют паркеты из невыпуклых семиугольников.

Паркеты из произвольных фигур

Существует несколько способов построения паркетов из произвольных фигур.

Способ первый. Берем уже известный нам паркет из правильных треугольников, шестиугольников, квадратов, или из произвольных многоугольников, и выполняем преобразования: сжатие/растяжение, замена прямолинейных отрезков кривыми с началом и концом в тех же точках, что у отрезков. На рис. 30 показаны паркеты, полученные их деформированных 4-х и 6-угольников.

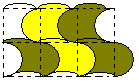
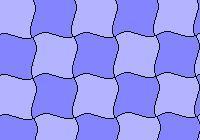
Рис. 30. Паркеты из деформированных правильных многоугольников.

Способ второй. Объединяем отдельные элементы уже существующих паркетов. Примеры: паркеты, полученные в результате объединения элементов квадратной сетки (рис. 31 а, б), паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников (рис. 31 в)

а б в

Рис. 31. Паркеты полученные объединением элементов существующих паркетов.

Способ третий. Берем существующий паркет и дополняем новыми линиями. Получаем разбиение плоскости на фигуры, которые затем можно по-новому объединить. Например, накладываем друг на друга две (или более) сетки уже известных паркетов, смещая или поворачивая одну сетку относительно другой; фигуры, образовавшиеся при пересечении линий, считаем элементами паркета. Пример, трансформация сетки из греческих крестов, причем сами греческие кресты получены из паркета, состоящего из обычных квадратов (рис.32):

Рис. 32. Паркеты, полученные преобразованием сетки из греческих крестов

Паркеты могут быть получены с помощью параллельного переноса звездчатых многоугольников (рис. 33):

Паркет (роспись стен) из звездчатых многоугольников (замок Блуа, Франция).

Рис. 33. Паркеты из звездчатых многоугольников.Совмещая вершины звездчатых многоугольников, получаем паркеты, состоящие из правильных восьмиугольников, равнобедренных прямоугольных треугольников, а также из звездчатых 16-угольников, напоминающих мальтийский крест.