2.2. Предел функции и его свойства

Пусть f(x) - функция непрерывного аргумента. Число A называется пределом функции y = f(x) при xx₀, если для каждого сколь угодно малого числа  >0 можно указать зависящее от  число () > 0 такое, что для всех х, удовлетворяющих неравенству x₀-х<, имеет место неравенство A - f(x) < . В формализованной форме это записывается так

(6)

(читается: f(x) стремится к A при х стремящимся к х₀). Наличие у функции f(x) предела A в точке х₀ содержательно означает, что как только независимая переменная х достаточно близко приблизится к значению х₀, так функция f(x) будет сколь угодно близка к A.

Справедливы следующие свойства пределов.

1. Если предел функции существует, то он единственен.

2. Предел постоянной величины равен самой постоянной.

3. Если при хx₀ существуют конечные пределы функций f(x) и g(x) , то

, где а и b числа.

4.

5.

В качестве примера вычислим два предела.

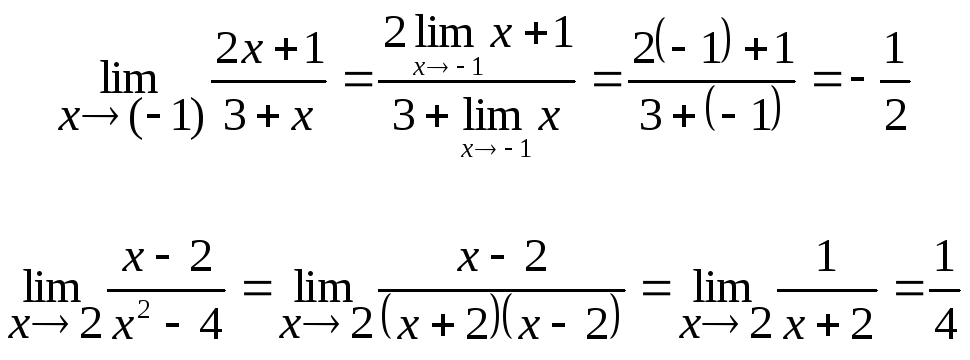
Функция f(x) называется непрерывной в точке х₀, если она определена в этой точке и некоторой ее окрестности, а также

(7)

Точки, в которых равенство (7) не выполняется, называются точками разрыва функции.

Все элементарные функции, а также любая их комбинация непрерывны в своей области определения. На практике непрерывные функции часто называют "хорошими функциями".

2.3. Определение производной

Значение функции в каждой допустимой фиксированной точке есть число. Изменяя значения аргумента, получим, в общем случае, различные значения функции. Как сильно изменится значение функции при данном изменении аргумента? Поиск ответа на этот вопрос приводит к понятию производной.

Пусть задана некоторая функция y = f(x). Выберем произвольное допустимое значение аргумента х и вычислим f(х). Затем, не выходя из области определения, изменим х на малую величину х. Вычислим f(х + x) и образуем отношение

(8)

Если существует конечный предел

то функция f(x) называется дифференцируемой в точке х, а значение предела называется производной от функции f(x) в точке х и обозначается

(9)

Значение производной зависит от выбранного значения точки х. Следовательно, производная - это функция от того же аргумента, что и f(x). Операцию вычисления производной называется дифференцированием функции.

.

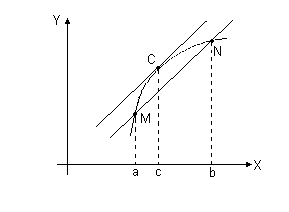
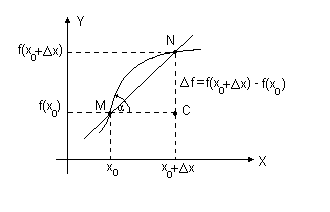
Рис. 2. Геометрический смысл производной

Рис. 3. Геометрический смысл формулы конечных приращений.

Рассмотрим геометрический смысл производной. Если изобразить на рисунке график функции f(x), то величина отношения (8) равна тангенсу угла наклона секущей графика к его оси абсцисс (см. рис. 2)

Если х  0, то точка N стремится к точке M и секущая MN стремится занять положение касательной к f(x) в точке M. Следовательно, значение производной f(x) в любой точке х области определения функции равно тангенсу наклона касательной к графику y = f(x) в точке с координатами х и f(x) к оси абсцисс.

Геометрический смысл производной позволяет пояснить важную формулу конечных приращений

f(b) - f(a) = f (c)(b -a). (10)

Действительно (см. рис. 3), на отрезке [a,b] всегда найдется точка с, в которой касательная параллельна секущей MN. В этом случае из построения следует формула (10), позволяющая выразить приращение функции через приращение аргументов и производную.