
- •Основы робототехники. Устройство роботов План лекции.
- •Лекция 1 Введение
- •Классификация роботов по назначению
- •Лекция 2 Кинематика манипулятора
- •Матрицы сложных поворотов
- •Лекция 3 Матрица поворота вокруг произвольной оси
- •Представление матриц поворота через углы Эйлера
- •Лекция 4 Геометрический смысл матриц поворота
- •Свойства матриц поворота
- •Однородные координаты и матрицы преобразований
- •Лекция 5 Звенья, сочленения и их параметры
- •Представление Денавита – Хартенберга
- •Алгоритм формирования систем координат звеньев
- •Для манипулятора Пума
- •Лекция 6 Уравнения кинематики манипулятора
- •Классификация манипуляторов
- •Обратная задача кинематики
- •Метод обратных преобразований
- •Лекция 7 Геометрический подход
- •Определение различных конфигураций манипулятора
- •Решение обратной задачи кинематики для первых трех сочленений
- •Решение для первого сочленения
- •Решение для второго сочленения
- •Лекция 8 Решение для третьего сочленения
- •Решение обратной задачи кинематики для последних трех сочленений
- •Решение для четвертого сочленения
- •Решение для пятого сочленения
- •Решение для шестого сочленения
- •Лекция 9 Уравнения вида конфигурации для определения индикаторов конфигурации манипулятора
- •Машинное моделирование
- •Динамика манипулятора
- •Метод Лагранжа-Эйлера
- •Скорость произвольной точки звена манипулятора
- •Лекция 10 Кинематическая энергия манипулятора
- •Потенциальная энергия манипулятора
- •Уравнение движения манипулятора
- •Уравнения движения манипулятора с вращательными сочленениями
- •Пример: двухзвенный манипулятор
- •Лекция 11 Уравнения Ньютона-Эйлера
- •Вращающиеся системы координат
- •Лекция 12 Подвижные системы координат
- •Кинематика звеньев
- •Лекция 13 Рекуррентные уравнения динамики манипулятора
- •Лекция 14 Планирование траекторий манипулятора
- •Сглаженные траектории в пространстве присоединенных переменных
- •Расчет 4-3-4 - траектории
- •Лекция 15 Граничные условия для 4-3-4-траекторий
- •Лекция 16 Управление манипуляторами промышленного робота
- •Метод вычисления управляющих моментов
- •Передаточная функция одного сочленения робота
- •Лекция 17 Устройство позиционирования для одного сочленения манипулятора
- •Критерии работоспособности и устойчивости
- •Лекция 18 Компенсация в системах с цифровым управлением
- •Зависимость момента от напряжения
- •Управление манипулятором с переменной структурой
- •Адаптивное управление
- •Адаптивное управление по заданной модели
- •Адаптивное управление с авторегрессивной моделью
- •Лекция 19 Адаптивное управление по возмущению
- •Независимое адаптивное управление движением
- •Лекция 20 очувствление Введение
- •Датчики измерения в дальней зоне
- •Триангуляция
- •Метод подсветки
- •Лекция 21 Измерение расстояния по времени прохождения сигнала
- •Очувствление в ближней зоне
- •Индуктивные датчики
- •Датчики Холла
- •Лекция 22 Емкостные датчики
- •Ультразвуковые датчики
- •Оптические датчики измерения в ближней зоне
- •Лекция 23 Тактильные датчики
- •Дискретные пороговые датчики
- •Аналоговые датчики
- •Силомоментное очувствление
- •Элементы датчика схвата, встроенного в запястье
- •Выделение сил и моментов
- •Лекция 24 Системы технического зрения
- •Получение изображения
- •Лекция 25 Методы освещения
- •Стереоизображение
- •Системы технического зрения высокого уровня
- •Сегментация
- •Проведение контуров и определение границ
Для манипулятора Пума
Шаг 1. Формирование базовой системы координат.
Сформировать правую ортонормированную систему координат (х0, y0, z0), связанную с основанием, ось z0 вдоль оси 1-го сочленения к «плечу» манипулятора. Оси х0 и y0 выбираются произвольно при условии их перпендикулярности оси z0.
Шаг 2. Начало и цикл. Для всех i ( i=1,2 … n-1) выполнить шаги 3-6.
Шаг 3. Формирование осей сочленения. Направить ось zi вдоль оси движения (вращательного или поступательного) i+1-го сочленения.
Шаг 4. Формирование начала i-й системы координат. Расположить начало i-й системы координат на пересечении осей zi и zi-1 или на пересечении общей нормали к осям zi и zi-1 с осью zi.
Шаг 5. Формирование оси xi. Выбрать единичный вектор xi следующим образом: xi = ±( zi-1 × zi)/ || zi-1 × zi || или вдоль общего перпендикуляра к осям zi-1 и zi, если они параллельны.
Шаг 6. Формирование оси yi Положить yi = +( zi × xi)/ ||zi ×xi|| , получив тем самым правостороннюю систему координат.
Шаг 7. Формирование системы координат схвата. Как правило, n-е сочленение является вращательным. Сформировать ось zn, направив ее вдоль оси zn-1 и от робота. Выбрать ось хn так, чтобы она была перпендикулярна осям zn-1 и zn.
Шаг 8. Определение параметров звеньев и сочленений. Для каждого i
(i =1…n) выполнить шаги 9-12.
Шаг 9. Определение di Расстояние di – от начала (i-1)-й системы координат до пересечения оси zi-1 с осью xi и началом i-й системы координат, отсчитываемой вдоль оси zi-1. Если i-е соединение – поступательное, то di – присоединенная переменная.
Шаг 10. Определение ai - расстояния между пересечением оси zi-1 с осью xi и началом i-й системы координат, отсчитываемой вдоль оси xi.
Шаг 11. Определение i – угла поворота оси xi -1 вокруг оси zi-1, чтобы она стала сонаправлена с осью xi. Если i-е сочленение – вращательное, то i-присоединенная переменная.
Шаг 12. Определение αi – угла поворота оси zi -1 вокруг оси xi, чтобы она стала сонаправлена с осью zi .
После построения ДХ-координат для всех звеньев можно построить однородные матрицы преобразования, связывающие i-ю и (i-1)-ю системы координат:
i-1Ai=
Tz,dTz,Tx,aTx,α=

 ×
×
× =
= .
(5-1)
.
(5-1)
Преобразуя (3-1), найдем, что матрица, обратная к i-1Аi, имеет вид:
 ,
(5-2)
,
(5-2)
где
![]() -
константы, а
-
константы, а
![]() -
присоединенная переменная, если
рассматриваемое сочленение – вращательное.
-
присоединенная переменная, если
рассматриваемое сочленение – вращательное.
Используя
матрицу
![]() ,
можно связать однородные координаты
рi
точки р
относительно i-й
системы координат (точка р
покоится в i–й
системе координат)с односторонними
координатами этой точки относительно
(i-1)-й
системы тсчета, связанной с (i-1)-м
звеном. Эта связь устанавливается
равенством:
,
можно связать однородные координаты
рi
точки р
относительно i-й
системы координат (точка р
покоится в i–й
системе координат)с односторонними
координатами этой точки относительно
(i-1)-й
системы тсчета, связанной с (i-1)-м
звеном. Эта связь устанавливается
равенством:
![]() ,
(5-3)
,
(5-3)
где
![]() и
и
![]() .
.
Для шестизвенного
манипулятора Пума были определены шесть
матриц
![]() ,
соответствующие показанным на рис. 5.4.
системам координат. Эти матрицы
представлены ниже:
,
соответствующие показанным на рис. 5.4.
системам координат. Эти матрицы
представлены ниже:
 ,
,
 ,
,
 ,
,
 ,
,
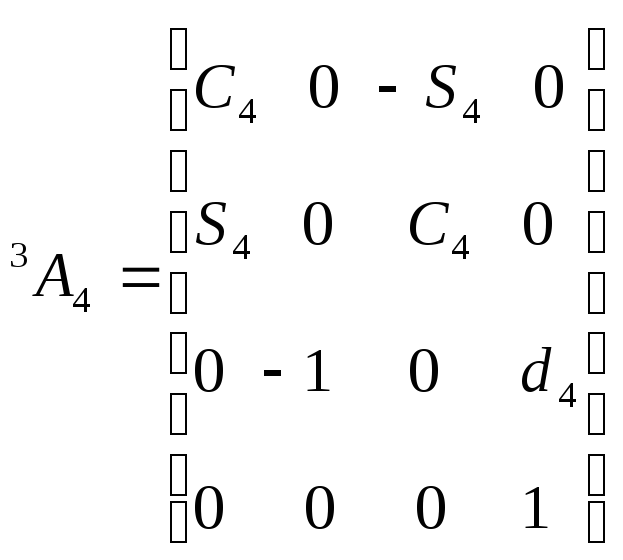
 ,
,
 ,
,
 ,
,
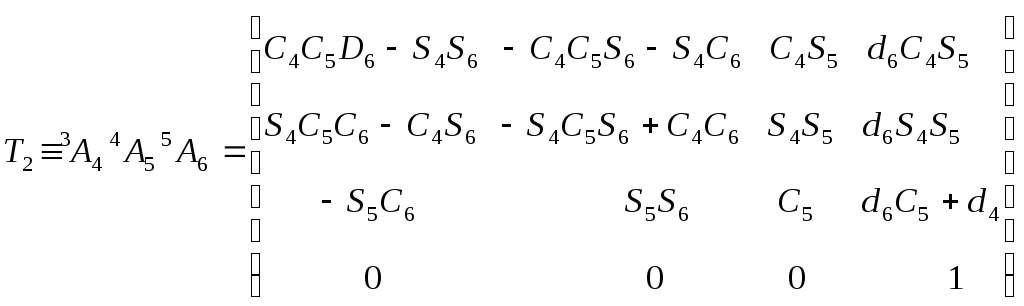 ,
,
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
