
- •9. Расчетные задания.
- •9.1. Линейная и векторная алгебра.
- •9.2. Аналитическая геометрия.
- •10. Тестовые задания для самостоятельной работы.
- •Задание 3. Найдите матрицу х из уравнений:
- •Задание 4. С помощью формул Крамера решить систему уравнений:
- •Задание 9. Найти координаты вектора векторного произведения векторов a и b.
- •2. Найти точку пересечения прямой и плоскости.
9. Расчетные задания.
9.1. Линейная и векторная алгебра.
Задание 1. Для матрицы третьего порядка вычислите ее определитель и определитель матрицы, транспонированной к данной.
1.
 ; 2.
; 2.
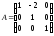 ;
3.
;
3.
 ;
;
4.
 ; 5.
; 5.
 ;
6.
;
6.
 ;
;
7.
 ; 8.
; 8.
 ;
9.
;
9.
 ;
;
10.
 ; 11.
; 11.
 ; 12.
; 12.
 ;
;
13.
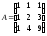 ; 14.
; 14.
 ; 15.
; 15.
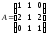 ;
;
16.
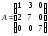 ; 17.
; 17.
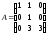 ;
18.
;
18.
 ;
;
19.
 ; 20.
; 20.
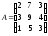 ;
21.
;
21.
 ;
;
22.
 ; 23.
; 23.
 ;
24.
;
24.
 ;
;
25.
 .
.
Задание 2. Вычислите определитель четвертого порядка
1.
 ; 2.
; 2. ; 3.
; 3.
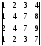 ;
;
4.
 ; 5.
; 5.
 ; 6.
; 6.
 ;
;
7.
 ; 8.
; 8.
 ; 9.
; 9.
 ;
;
10.
 ; 11.
; 11.
 ;
12.
;
12.
 ;
;
13.
 ;
14.
;
14.
 ;
15.
;
15.
 ;
;
16.
 ;
17.
;
17.
 ;
18.
;
18.
 ;
;
19.
 ;
20.
;
20.
 ;
21.
;
21.
 ;
;
22.
 ;
23.
;
23.
 ;
24.
;
24.
 ;
;
25.
 .
.
Задание 3. Найдите матрицу, обратную матрице. Проверьте результат,
вычислив произведение взаимно обратных матриц.
1.
 ; 2.
; 2.
 ;
;
3.
 ; 4.
; 4.
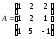 ;
;
5.
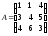 ; 6.
; 6.
 ;
;
7.
 ; 8.
; 8.
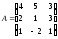 ;
;
9.
 ; 10.
; 10.
 ;
;
11.
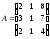 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14. ;
;
15.
 ; 16.
; 16. ;
;
17.
 ; 18.
; 18. ;
;
19.
 ; 20.
; 20.
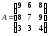 ;
;
21.
 ; 22.
; 22. ;
;
23.
 ; 24.
; 24.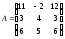 ;
;
25.
 .
.
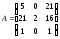
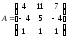
Задание 4. Решите систему линейных уравнений матричным способом.
1.
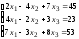 ; 2.
; 2.
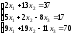 ;
;
3.
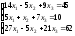 ; 4.
; 4.
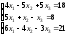 ;
;
5.
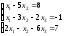 ; 6.
; 6.
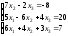 ;
;
7.
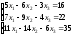 ; 8.
; 8.
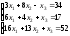 ;
;
9.
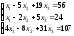 ; 10.
; 10.
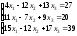 ;
;
11.
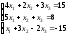 ; 12.
; 12.
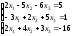 ;
;
13.
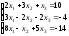 ; 14.
; 14.
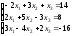 ;
;
15.
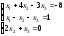 ; 16.
; 16.
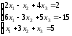 ;
;
17.
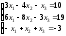 ; 18.
; 18.
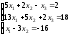 ;
;
19.
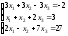 ; 20.
; 20.
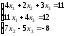 ;
;
21.
 ; 22.
; 22.
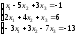 ;
;
23.
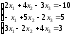 ; 24.
; 24.
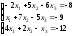 ;
;
25.
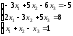 .
.
Задание 5. Решите систему линейных уравнений по формулам Крамера.
1.
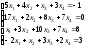 ;
2.
;
2.
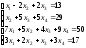 ;
;
3.
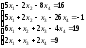 ;
4.
;
4.
 ;
;
5.
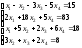 ;
6.
;
6.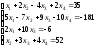 ;
;
7.
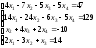 ;
8.
;
8.
 ;
;
9.
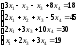 ;
10.
;
10.
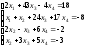 ;
;
11.
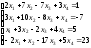 ;
12.
;
12.
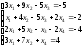 ;
;
13.
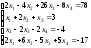 14.
14.
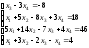 ;
;
15.
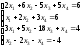 ;
16.
;
16.
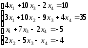 ;
;
17.
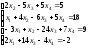 ;
18.
;
18.
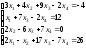 ;
;
19.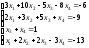 ;
20.
;
20.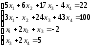 ;
;
21.
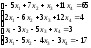 ;
22.
;
22.
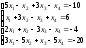 ;
;
23.
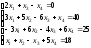 24.
24.
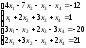 ;
;
25.
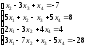 .
.
Задание 6. Решите линейную однородную систему уравнений.
1.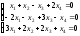 ; 2.
; 2.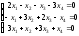 ;
;
3.
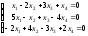 ; 4.
; 4.
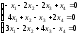 ;
;
5.
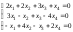 ; 6.
; 6.
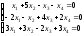 ;
;
7.
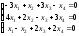 ; 8.
; 8.
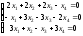 ;
;
9.
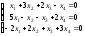 ; 10.
; 10.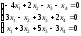 ;
;
11.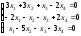 ; 12.
; 12.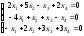 ;
;
13.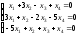 ; 14.
; 14.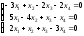 ;
;
15.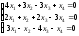 ; 16.
; 16.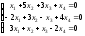 ;
;
17.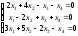 ; 18.
; 18.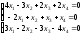 ;
;
19.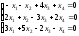 ; 20.
; 20.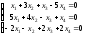 ;
;
21.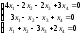 ; 22.
; 22.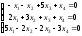 ;
;
23.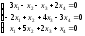 ; 24.
; 24.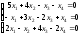 ;
;
25.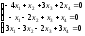 .
.
Задание 7. Дана расширенная матрица системы. Найдите решение этой системы и соответствующей ей однородной системы.
1.
 ; 2.
; 2.
 ;
;
3.
 ; 4.
; 4.
 ;
;
5.
 ; 6.
; 6.
 ;
;
7.
 ; 8.
; 8.
 ;
;
9.
 ; 10.
; 10.
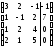 ;
;
11.
 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14.
 ;
;
15.
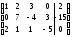 ; 16.
; 16.
 ;
;
17.
 ; 18.
; 18.
 ;
;
19.
 ; 20.
; 20.
 ;
;
21.
 ; 22.
; 22.
 ;
;
23.
 ; 24.
; 24.
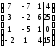 ;
;
25.
 .
.
Задание 8. Даны координаты векторов а1, а2, а3, а4 и b в некотором базисе. Покажите, что векторы а1, а2, а3, а4 образуют базис и найдите координаты вектора b в этом базисе.
-
а1(1,2,-1,-2); а2(2,3,0,1); а3(1,2,1,3); а4(1,3,-1,0);b(7,14,-1,2).
-
а1(2,1,0,-1); а2(2,3,0,-2); а3(2,4,2,1); а4(0,-3,0,2);b(5,2,1,0).
-
а1(1,1,4,2); а2(2,-1,3,1); а3(0,2,0,0); а4(1,-1,0,1);b(5,0,0,5).
-
а1(1,2,3,4); а2(2,3,4,1); а3(3,4,1,2); а4(4,1,2,3);b(2,2,2,4).
-
а1(2,0,0,0); а2(0,4,0,0); а3(0,0,6,0); а4(0,0,0,8);b(6,7,0,1).
-
а1(1,2,-1,-2); а2(2,3,0,1); а3(1,2,1,3); а4(1,3,-1,0);b(6,7,0,1).
-
а1(2,1,0,-1); а2(2,3,0,-2); а3(2,4,2,1); а4(0,-3,0,2);b(-3,2,5,0).
-
а1(2,3,4,5); а2(3,4,5,2); а3(4,5,2,3); а4(5,2,3,4);b(-1,2,1,-2).
-
а1(3,5,-1,-1); а2(3,5,1,4); а3(2,5,0,3); а4(1,3,-1,0);b(7,14,-1,2).
-
а1(4,4,0,-3); а2(4,7,2,-1); а3(2,1,2,3); а4(0,-3,0,2);b(5,2,1,0).
-
а1(3,0,7,3); а2(2,1,3,1); а3(1,1,0,1); а4(1,-1,0,1);b(5,0,0,5).
-
а1(3,5,7,5); а2(5,7,5,3); а3(7,5,3,5); а4(4,1,2,3);b(2,2,2,4).
-
а1(2,4,0,0); а2(0,4,6,0); а3(0,0,6,8); а4(0,0,0,8);b(-14,6,0,1).
-
а1(1,2,-1,-2); а2(3,5,-1,-1); а3(3,5,1,4); а4(2,5,0,3);b(6,7,0,1).
-
а1(2,1,0,-1); а2(4,4,0,-3); а3(2,7,2,-1); а4(2,1,2,3);b(-3,2,5,0).
-
а1(5,7,9,7); а2(7,9,7,5); а3(9,7,5,7); а4(5,2,3,4);b(-1,2,1,-2).
-
а1(1,3,5,3); а2(3,5,3,2); а3(5,3,1,3); а4(3,0,1,2);b(-6,0,2,-3).
-
а1(-1,1,3,1); а2(1,3,1,-1); а3(3,-1,-1,1); а4(2,-1,0,1);b(-3,6,7,-2).
-
а1(0,1,2,3); а2(1,2,3,0); а3(2,3,0,1); а4(3,0,1,2);b(-6,0,2,-3).
-
а1(-1,0,1,2); а2(0,1,2,-1); а3(1,2,-1,0); а4(2,-1,0,1);b(-3,6,7,-2).
-
а1(4,4,3,0); а2(-17,24,1,1); а3(-6,-1,2,0); а4(-5,3,1,0);b(-9,10,1,1).
-
а1(2,2,7,7); а2(-9,-7,-6,-17); а3(-4,-2,2,1); а4(-3,-1,0,2);b(-15,-7,17,14).
-
а1(2,4,2,1);а2(-10,-9,-7,-5);а3(0,10,0,-2);а4(-4,3,-1,0);b(-42,-43,-39,23).
-
а1(3,3,4,1); а2(-1,-8,-7,2); а3(0,5,14,-3); а4(0,1,5,-1);b(9,31,34,-5).
-
а1(8,3,2,5); а2(-26,1,2,-5); а3(4,2,1,6); а4(-2,1,0,2);b(14,17,12,27).
