10 Прямая и точка в плоскости
Давайте вспомним, когда прямая принадлежит плоскости:
1) прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости;
2) прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости и параллельна какой-нибудь прямой этой плоскости.
Из этих двух известных Вам признаков принадлежности прямой плоскости можно сделать следующие выводы:
1) если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой лежат на одноименных следах плоскости;
2) прямая принадлежит плоскости, если она с одним следом плоскости имеет общую точку, а другому следу параллельна.
Рассмотрим плоскость Q, общего положения, задана следами, рисунок 52. Прямая NM принадлежит этой плоскости, поскольку ее следы лежат на одноименных следах плоскостей. На рисунке 53 показан эпюр плоскости, заданной пересекающимися прямыми t и n. Чтобы построить прямую, лежащую в этой плоскости, достаточно провести произвольно одну из проекций, например, горизонтальную c1, а затем спроецировть точки пересечения этой прямой с прямыми плоскости на фронтальную плоскость. Фронтальная проекция прямой c2 пройдет через полученные точки.
Рисунок 52 Рисунок 53
Согласно второму положению на рисунке 54 построена прямая h, принадлежащая плоскости Р, - она имеет точку N (N1, N2) общую с плоскостью Р и параллельна прямой, лежащей в плоскости - горизонтальному следу Р1.
Рисунок 54 Рисунок 55
Рассмотрим плоскости частного положения. Если прямая или фигура принадлежит горизонтально-проецирующей плоскости, то горизонтальные проекции этих геометрических элементов совпадают с горизонтальным следом плоскости.
Если прямая или плоская фигура принадлежит фронтально-проецирующей плоскости, то фронтальные проекции этих геометрических элементов совпадают с фронтальным следом плоскости.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
ЗАДАЧА 1. Дана плоскость Р (a || b). Известна горизонтальная проекция точки В, принадлежащей плоскости Р. Постройте фронтальную проекцию точки В, рисунок 56. На рисунках 57, 58, 59 показано фрагментарно решение этой задачи: 1) Проведем через В1 (известную проекцию точки В) любую прямую,
лежащую в плоскости Р, - для этого прямая должна иметь с плоскостью две общие точки. Отметим их на чертеже - М1 и K1.
-
Построим фронтальные проекции этих точек по принадлежности точек прямым, т. е. М2 на прямой а, K2 на прямой b. Проведем через фронтальные проекции точек фронтальную проекцию прямой.
Рисунок 56 Рисунок 57
-
По признаку принадлежности точки плоскости, построим фронтальную проекцию точки В на прямой М2K2.
Т. о. точка В принадлежит плоскости Р так как она лежит на прямой, принадлежащей этой плоскости.
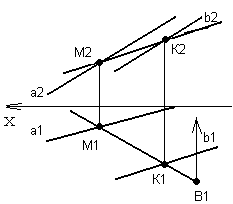
Рисунок 58 Рисунок 59
11 Особые прямые в плоскости
Прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций называется горизонталью; прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций называется фронталью.
Все горизонтали одной плоскости параллельны между собой и параллельны горизонтальному следу плоскости. Все фронтали одной плоскости параллельны между собой и параллельны фронтальному следу плоскости.
На рисунке 60 построена горизонталь в плоскости Р, заданной следами. Фронтальная проекция горизонталь h2 всегда параллельна оси ОХ.
На рисунке 61 построена фронталь в плоскости треугольника АВС. Горизонтальная проекция фронтали f1 всегда параллельна оси ОХ.
Рисунок 60 Рисунок 61