Нелинейная регрессия

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

• регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

• полиномы разных степеней - ;

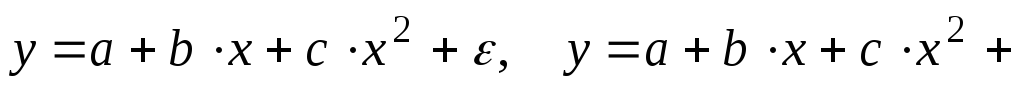
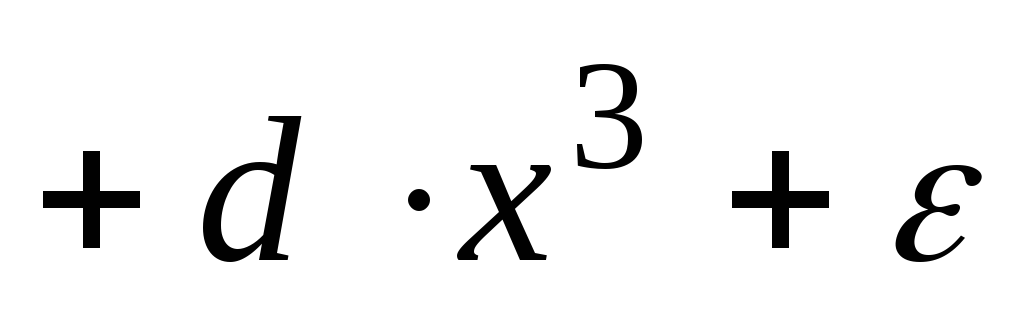• равносторонняя гипербола - .

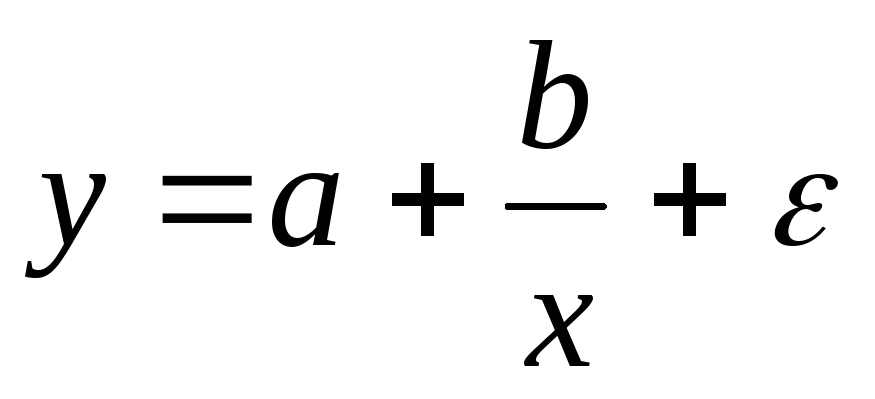К нелинейным регрессиям по оцениваемым параметрам относятся функции:

• степенная - ;

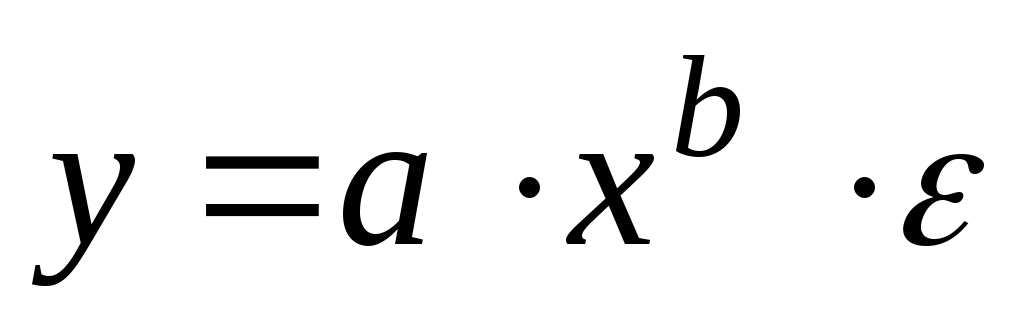• показательная - ;

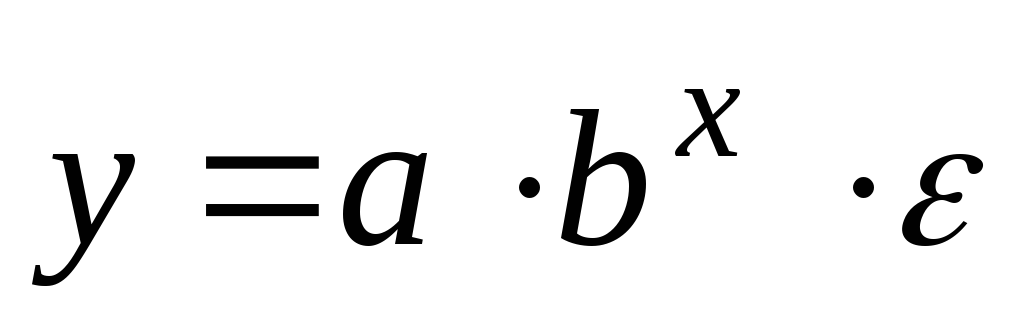• экспоненциальная - .

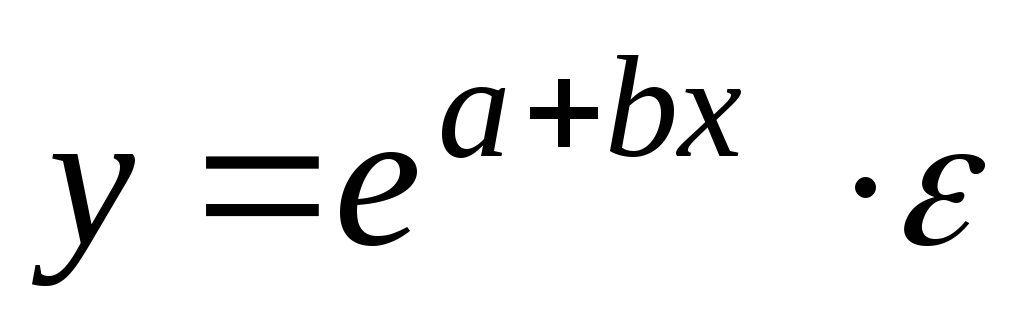Нелинейная регрессия по включенным переменным определяется, как и линейная, методом наименьших квадратов, так как функции линейны по параметрам.

Так в параболе , заменяя переменные , получим двухфакторное уравнение линейной регрессии:

,

для оценки параметров которого используется метод наименьших квадратов. По аналогии для полинома третьего порядка получим трехфакторную модель линейной регрессии.

Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценки параметров и проверки гипотез. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.

Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака.

Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.

При и кривая симметрична относительно высшей точки, т.е. точки перелома кривой, изменяющей направление связи, а именно рост на падение. Такого рода функцию можно наблюдать в экономике труда при изучении зависимости заработной платы работников физического труда от возраста – с увеличением возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы работника.

При и парабола второго порядка симметрична относительно своей низшей точки, что позволяет определить минимум функции в точке, меняющей направление связи, т.е. снижение на рост.

Ввиду симметричности кривой парабола второй степени далеко не всегда пригодна в конкретных исследованиях. Чаще исследователь имеет дело с отдельными сегментами параболы, а не с полной параболической формой. Кроме того, параметры параболической связи не всегда могут быть логически истолкованы. Поэтому если график зависимости не демонстрирует четко выраженной параболы второго порядка (нет смены направленности связи признаков), то она может быть заменена другой нелинейной функцией, например степенной.

Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются методом наименьших квадратов, следует назвать равностороннюю гиперболу: . Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y:

.

Для равносторонней гиперболы виды , заменив на z, получим линейное уравнение регрессии , оценка параметров которого может быть дана методом наименьших квадратов. Система нормальных уравнений составит:

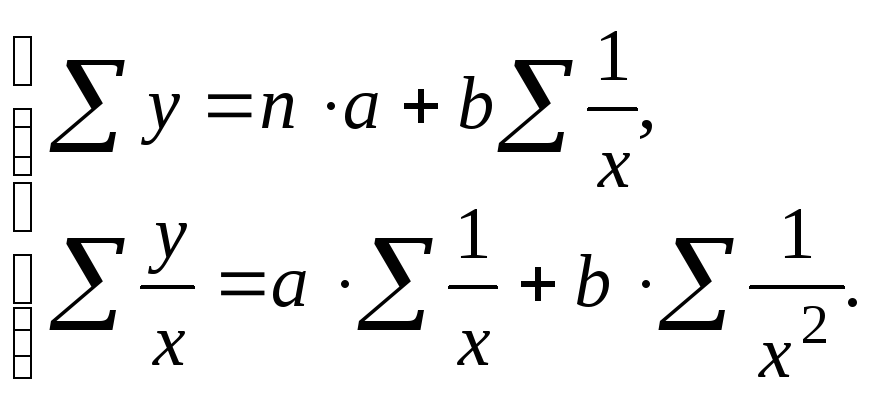
При имеем обратную зависимость, которая при характеризуется нижней асимптотой, т.е. минимальным предельным значением y, оценкой которого служит параметр a. Так для кривой Филлипса величина параметра a, равная 0,00679, означает, что с ростом уровня безработицы темп прироста заработной платы в пределе стремится к нулю. Соответственно можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.

При имеем медленно повышающуюся функцию с верхней асимптотой при , т.е. с максимальным предельным уровнем y, оценку которого дает параметр a.

Примером может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Математическое описание подобного рода взаимосвязей получило название кривых Энгеля. С ростом дохода доля доходов, расходуемых на продовольствие, уменьшается. Соответственно с увеличением дохода доля доходов, расходуемых на непродовольственные товары, будет возрастать. Однако это увеличение не беспредельно, ибо на все товары сумма долей не может быть дольше единицы. Соответственно можно определить границу величины дохода, дальнейшее увеличение которого не приводит к росту доли расходов на отдельные непродовольственные товары.

Однако для описания кривой Энгеля можно также использовать полулогарифмическую кривую . Данная регрессия также сводится к исследованию линейной заменой .

Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейная, то она не может быть сведена к линейной функции, например: или .

В исследованиях по регрессионному анализу относят к нелинейным лишь внутренне нелинейные по оцениваемым параметрам. А все остальные относятся к классу линейных моделей.

Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Итак, для нелинейных моделей приведем процедуру регрессионного анализа:

1. Принимаются некоторые правдоподобные исходные значения параметров.

2. Вычисляются предсказанные значения y по фактическим значениям x с использованием этих значений параметров.

3. Вычисляются остатки для всех наблюдений в выборке и, следовательно, S – сумма квадратов отклонений.

4. Вносятся небольшие изменения в одну или более оценку параметров.

5. Вычисляются новые предсказанные значения y, остатки и S.

6. Если S меньше, чем прежде, то новые оценки параметров лучше прежних и их следует использовать в качестве новой отправной точки.

7. Шаги 4, 5 и 6 повторяют вновь до тех пор, пока не окажется невозможным внести такие изменения в оценки параметров, которые привели бы к уменьшению S.

8. Делается вывод о том, что величина S минимизирована и конечные оценки параметров являются оценками по методу наименьших квадратов.

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция . Это связано с тем, что параметр b в ней имеет четкое экономическое истолкование, т.е. он является коэффициентом эластичности. Это означает, что величина коэффициента показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную значению коэффициента b.

Поскольку коэффициенты эластичности представляют экономический интерес, а виды моделей не ограничиваются только степенной функцией, приведем формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии.

Вид функции, y	Первая производная,	Коэффициент эластичности,
Линейная	b
Парабола второго порядка
Гипербола
Показательная
Степенная
Полулогарифмическая
Логистическая
Обратная