
Метод наименьших квадратов (Ordinary least squares method, ols)
Метод наименьших квадратов имеет две постановки: геометрическую и статистическую. Обратимся в начале к геометрической.
Итак,
имеется набор наблюдений
![]() Задача геометрии состоит в поиске
наилучшего приближения. Измерение
расстояния от точек наблюдения возможно
по вертикали, т.е. по координате y,
либо как перпендикуляр до прямой. Тогда
расстояния:
Задача геометрии состоит в поиске
наилучшего приближения. Измерение
расстояния от точек наблюдения возможно
по вертикали, т.е. по координате y,
либо как перпендикуляр до прямой. Тогда
расстояния:
![]() .
На этом этапе возможна оценка различными
методами. Но если использовать, например,
в качестве оценки сумму модулей
расстояний, то задача может иметь
несколько решений. В то время, как
квадратичная функция (метод наименьших
квадратов) дает единственное решение.
.
На этом этапе возможна оценка различными
методами. Но если использовать, например,
в качестве оценки сумму модулей
расстояний, то задача может иметь
несколько решений. В то время, как
квадратичная функция (метод наименьших
квадратов) дает единственное решение.
Рассмотрим минимизацию функционала
![]() .
.
Для этого необходимо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю.
![]()
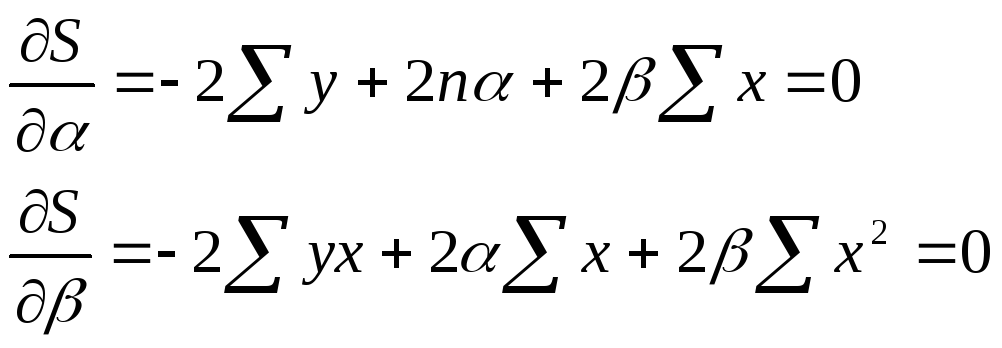
Таким образом,

![]() ,
,
![]() ,
,
![]() .
.
Возможность четкой интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Формально a – значение y при x=0. Если признак-фактор не имеет и не может иметь нулевого значения, то трактовка свободного члена не имеет смысла. Параметр a может не иметь экономического содержания.
Рассмотрим еще раз сумму:
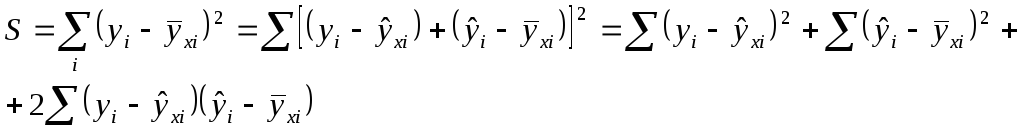
Удвоенная сумма равна нулю. Это вытекает из геометрической постановки задачи.
И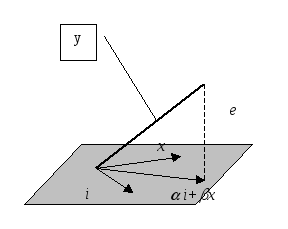 так,
i
и x
- не коллинеарны. В противном случае
все x
постоянны, задача не имеет смысла.
Остатки должны быть перпендикулярны
плоскости. Тогда сумма всех остатков
должна давать 0. Кроме того, плоскость
регрессоров должна включать единичный
вектор. Иногда эта константа включается
неявно. Т.е. например, имеется два
регрессора. Но дополнительное условие,
что они в сумме дают 1.
так,
i
и x
- не коллинеарны. В противном случае
все x
постоянны, задача не имеет смысла.
Остатки должны быть перпендикулярны
плоскости. Тогда сумма всех остатков
должна давать 0. Кроме того, плоскость
регрессоров должна включать единичный
вектор. Иногда эта константа включается
неявно. Т.е. например, имеется два
регрессора. Но дополнительное условие,
что они в сумме дают 1.
Далее вводятся следующие обозначения:
![]() -
total summ square;
-
total summ square;
![]() -
error summ square;
-
error summ square;
![]() -
regression
summ
square.
-
regression
summ
square.
Уравнение регрессии всегда дополняется показателем тесноты связи. При исследовании линейной регрессии таким показателем выступает коэффициент корреляции.
![]() .
.
Линейный
коэффициент корреляции находится в
границах
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
а при
,
а при
![]() ,
,
![]() .
.
Величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в линейной форме. Поэтому близость к нулю не означает отсутствия связи между признаками. Хотя это верно не для всех моделей. Например, при рассмотрении задачи, x и y являются временными рядами, возможно, что коэффициент детерминации близок к 1, но связи между рядами нет, коэффициент просто указывает, что оба ряда растут. В то же время, если объяснять доходы семьи расходами, то коэффициент 0,1 достаточно велик. Т.е. этот коэффициент важен для прогноза, а для самого значения константы он не важен.
Обычно
при исследовании такой модели
рассчитывается квадрат линейного
коэффициента корреляции
![]() ,
называемый коэффициентом детерминации.
Он характеризует долю дисперсии
результативного признака y,
объясняемую регрессией, в общей дисперсии
результативного признака.
,
называемый коэффициентом детерминации.
Он характеризует долю дисперсии
результативного признака y,
объясняемую регрессией, в общей дисперсии
результативного признака.
Свойства коэффициентов регрессии существенным образом зависят от случайной составляющей. Для того, чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие результаты, случайный член должен удовлетворять четырем условиям, известным как условия Гаусса-Маркова.
-
 для
всех наблюдений.
для
всех наблюдений.
Математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Т.е. он не должен иметь систематического смещения ни в одном из двух возможных направлений.
-
 постоянна
для всех дисперсий.
постоянна
для всех дисперсий.
Дисперсия
случайного члена должна быть постоянна
для всех наблюдений. Не должно быть
априорной причины для того, чтобы он
порождал большую ошибку в одних
наблюдениях, чем в других. В силу первого
условия
![]() .
.
Это условие гомоскедастичности. В противном случае, если дисперсия не является постоянной величиной, то выполняется гетероскедастичность.
Величина
![]() неизвестна. Одна из задач регрессионного
анализа состоит в оценке стандартного
отклонения случайного члена.
неизвестна. Одна из задач регрессионного
анализа состоит в оценке стандартного
отклонения случайного члена.
В случае невыполнения этого условия, коэффициенты регрессии, найденные по обычному методу наименьших квадратов (МНК), будут неэффективны. Т.е. можно получить более надежные коэффициенты другим методом.
Это
условие предполагает отсутствие
систематической связи между значениями
случайного члена в любых двух наблюдениях.
Данное условие можно переписать в виде:
![]() .
Если это условие не будет выполнено, то
регрессия опять даст неэффективные
результаты. Это условие отсутствие
автокорреляции ошибок. Практически не
выполняется в задачах с временными
рядами, например, о доходности ГКО.
.
Если это условие не будет выполнено, то
регрессия опять даст неэффективные
результаты. Это условие отсутствие
автокорреляции ошибок. Практически не
выполняется в задачах с временными
рядами, например, о доходности ГКО.
4)
Случайный член должен быть распределен
независимо от объясняющих переменных.
Значения любой независимой переменной
в каждом наблюдении должно считаться
экзогенным, полностью определяемым
внешними причинами, не учитываемыми в
уравнении регрессии. Тогда теоретическая
ковариация между независимой переменной
и случайным членом равна нулю, и т.к.
![]() ,
то
,
то
![]()
Теорема Гаусса-Маркова.
В предположениях модели 1-3аб:
-
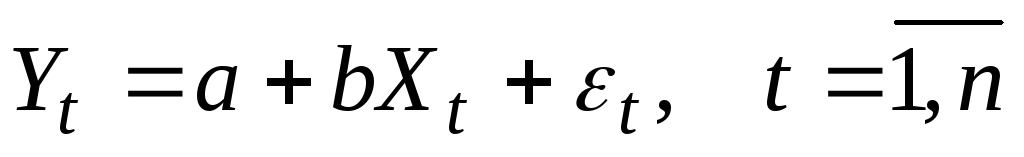
-
 -
детерминированная величина
-
детерминированная величина
3а.
![]()
3б.
![]()
оценки
![]() :
:
![]() ,
полученные по методу наименьших
квадратов, имеют наименьшую дисперсию
в классе всех линейных несмещенных
оценок. (Т.е. являются наилучшими в
некотором смысле. Best
Linear
Unbaised
Estimator
– BLUE).
,
полученные по методу наименьших
квадратов, имеют наименьшую дисперсию
в классе всех линейных несмещенных
оценок. (Т.е. являются наилучшими в
некотором смысле. Best
Linear
Unbaised
Estimator
– BLUE).
Доказательство:
-
Проверим несмещенность оценок:
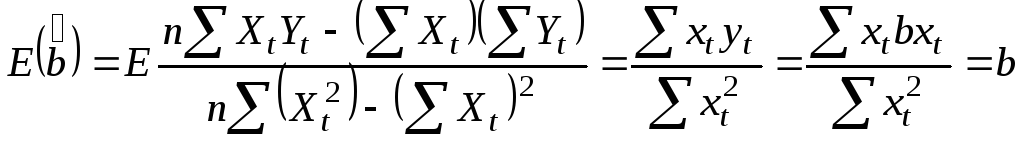 .
.
![]() .
.
![]() .
.
-
Вычислим дисперсии оценок
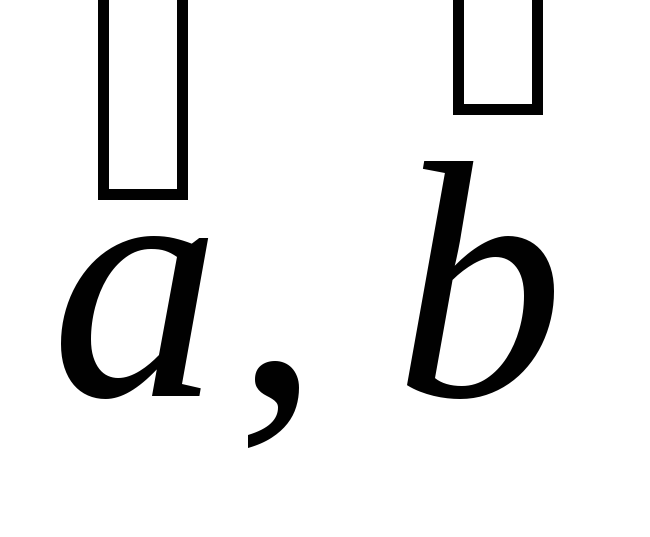 .
.
Представим
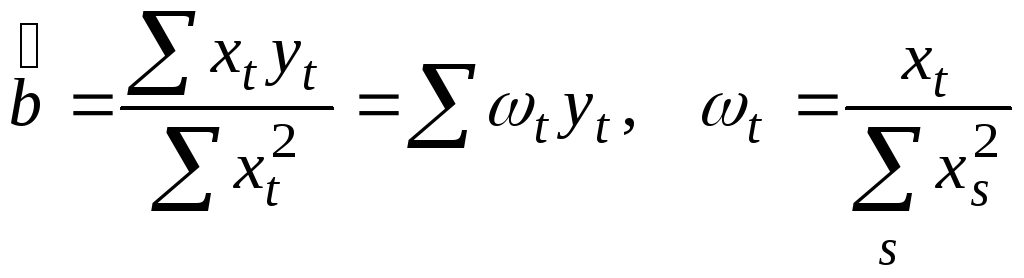
(самостоятельно проверить выполнение условий 1)-4) )
![]() ,
,
![]() ,
,
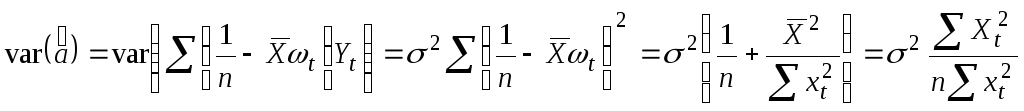 ,
,
используя
![]() .
.
Тогда
можно показать (самостоятельно), что
![]() .
.
3. Покажем, что МНК-оценки являются наилучшими (в смысле наименьшей дисперсии) в классе всех линейных несмещенных оценок.
Пусть
![]() - другая несмещенная оценка,
- другая несмещенная оценка,
![]() ,
тогда
,
тогда
![]() ,
,
тогда
![]() ,
,
![]()
![]() .
.
В
выкладках использованы следующие
формулы:
![]() из определения
из определения
![]() и
и
![]() .
.
Аналогично, можно показать
![]() (самостоятельно).
(самостоятельно).
Оценим
еще один параметр регрессионного
уравнения – дисперсию ошибок. Остатки
регрессии определяются из уравнения
![]() .
Остатки регрессии так же, как и ошибки
.
Остатки регрессии так же, как и ошибки
![]() являются случайными величинами, однако
разница состоит в том, что они наблюдаемы.
являются случайными величинами, однако
разница состоит в том, что они наблюдаемы.
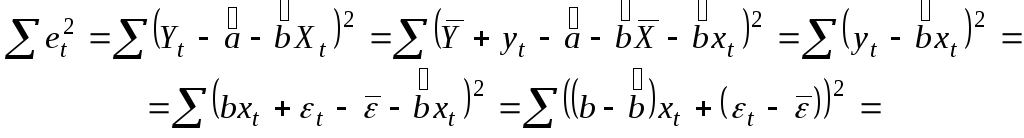
![]() .
.
Вычислим
мат. ожидание
![]() .
.
![]() .
.
Используя
соотношение
![]() .
.
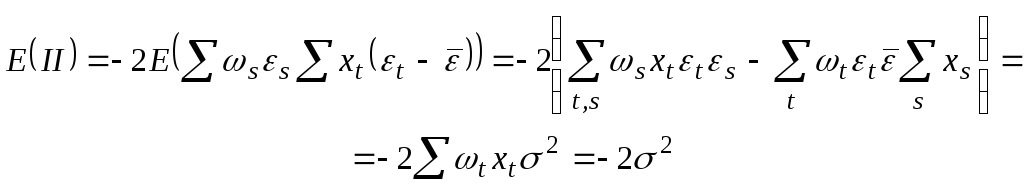
![]() .
.
Таким
образом,
![]() .
.
Отсюда следует, что
![]()
является
несмещенной оценкой дисперсии ошибок
![]() .
.
Как правило, на практике дисперсия ошибок неизвестна, поэтому вместо нее используется оценка, тогда формулы приобретают вид
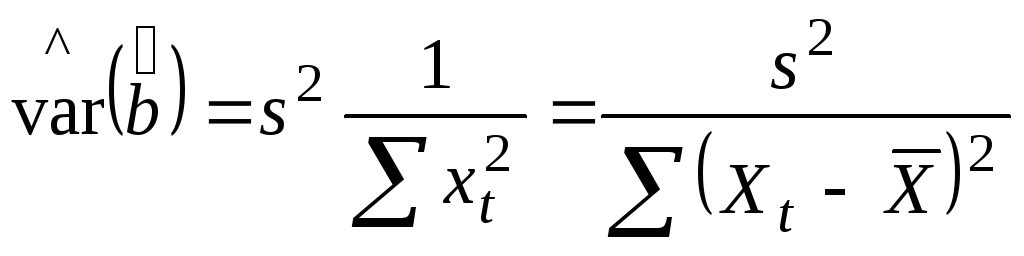 ;
;
 ;
;
![]() .
.
Следующим этапом делается еще одно предположение:
4’) Предположение нормальности.
Наряду с условиями Гаусса-Маркова обычно также предполагается нормальное распределение случайного члена. Если случайный член распределен нормально, то так же будут распределены и коэффициенты регрессии.
![]() .
Тогда из некоррелированности следует
независимость. В силу того, что оценка
коэффициента линейна по
.
Тогда из некоррелированности следует
независимость. В силу того, что оценка
коэффициента линейна по
![]() ,
то и
,
то и
![]() имеет нормальное распределение.
имеет нормальное распределение.
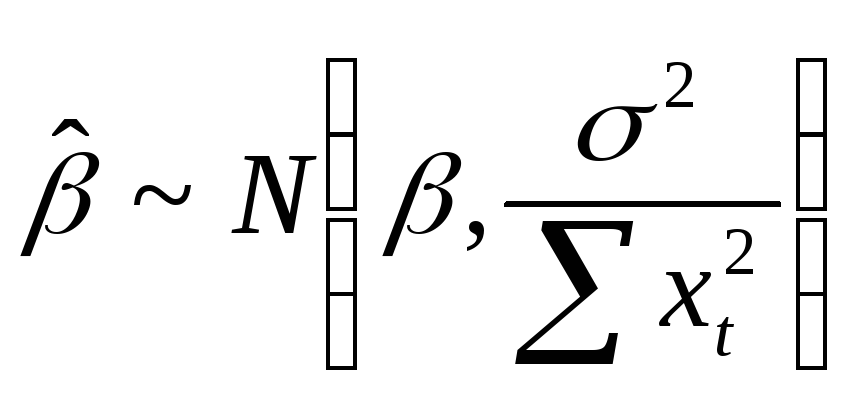 .
А значит, и оценка второго параметра
имеет нормальное распределение.
.
А значит, и оценка второго параметра
имеет нормальное распределение.
![]() .
(доказать)
.
(доказать)
Тогда
статистика
 имеет распределение Стьюдента с n-2
степенями свободы, но только в том
случае, если числитель и знаменатель
независимы. Тестирование гипотезы
происходит по стандартной схеме.
имеет распределение Стьюдента с n-2
степенями свободы, но только в том
случае, если числитель и знаменатель
независимы. Тестирование гипотезы
происходит по стандартной схеме.
