
Оценка существенности параметров линейной корреляции и регрессии.
Будем считать, что
формулирование гипотезы предшествует
эксперименту, и что уже есть некоторая
гипотетическая связь или зависимость.
Например, что зависимость выражена
регрессией:
![]() .
Пусть выдвигается гипотеза о том, что
.
Пусть выдвигается гипотеза о том, что
![]() ,
тогда вторая гипотеза
,
тогда вторая гипотеза
![]() .
.
Или иначе, можно
установить наличие зависимости величины
y
от x,
используя для этого следующую процедуру.
В качестве нулевой гипотезы принимается,
что y
не зависит от x,
т.е. что
![]() .
Альтернативная гипотеза заключается
в том, что
.
Альтернативная гипотеза заключается
в том, что
![]() ,
т.е. x
влияет на y.
Если можно отвергнуть нулевую гипотезу,
то таким образом устанавливается наличие
зависимости.
,
т.е. x
влияет на y.
Если можно отвергнуть нулевую гипотезу,
то таким образом устанавливается наличие
зависимости.
Дальше будем
рассматривать парную регрессию. В
нулевой гипотезе будет утверждать
![]() ,
альтернативная гипотеза
,
альтернативная гипотеза
![]() .
Будем полагать, что что четыре условия
Гаусса-Маркова выполняются.
.
Будем полагать, что что четыре условия
Гаусса-Маркова выполняются.
Если гипотеза
![]() верна, то оценки
верна, то оценки
![]() ,
полученные в ходе регрессионного
анализа, будут иметь распределение с
математическим ожиданием
,
полученные в ходе регрессионного
анализа, будут иметь распределение с
математическим ожиданием
![]() и дисперсией
и дисперсией
![]() .
Далее допустим, что остаточный член u
распределен нормально, в этом случае
величина
.
Далее допустим, что остаточный член u
распределен нормально, в этом случае
величина
![]() также будет нормально распределена,
тогда (учитывая структуру нормального
распределения -
также будет нормально распределена,
тогда (учитывая структуру нормального
распределения -
![]() )
большинство оценок параметра
)
большинство оценок параметра
![]() будет находиться в пределах двух
стандартных отклонений от
будет находиться в пределах двух
стандартных отклонений от
![]() (если верна гипотеза
(если верна гипотеза
![]() ).
).
Рассмотрим пример
на модели общей инфляции
![]() .
Темпы общей инфляции
.
Темпы общей инфляции
![]() (в процентах) в экономике зависят от
темпов инфляции, вызванной ростом
заработной платы (
(в процентах) в экономике зависят от
темпов инфляции, вызванной ростом
заработной платы (![]() ,
в процентах). Рассмотрим гипотезу о том,
что без учета эффектов, вносимых случайным
членом, общая инфляция равна инфляции,
вызванной ростом заработной платы, т.е.
нулевая гипотеза
,
в процентах). Рассмотрим гипотезу о том,
что без учета эффектов, вносимых случайным
членом, общая инфляция равна инфляции,
вызванной ростом заработной платы, т.е.
нулевая гипотеза
![]() и
и
![]() .
.
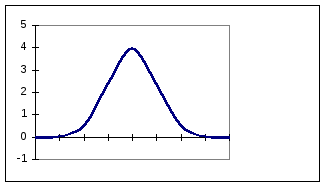 Тогда,
если нулевая гипотеза верна, то оценки
коэффициентов регрессии распределены
следующим образом (см. рис.). При
справедливости нулевой гипотезы оценка
будет находиться приблизительно между
0,8 и 1,2.
Тогда,
если нулевая гипотеза верна, то оценки
коэффициентов регрессии распределены
следующим образом (см. рис.). При
справедливости нулевой гипотезы оценка
будет находиться приблизительно между
0,8 и 1,2.
0,7
0,8 0,9 1,0 1,1 1,2 1,3![]() ,
используя регрессионный анализ. Допустим,
что оценка значительно отличается от
1. Допустим, что она равна 0,7. Это составит
три стандартных отклонения от 1.
Вероятность того, что отличие от среднего
достигнет трех стандартных отклонений
в положительную или отрицательную
сторону, составляет 0,0027. На этом основании
можно сделать два вывода:
,
используя регрессионный анализ. Допустим,
что оценка значительно отличается от
1. Допустим, что она равна 0,7. Это составит
три стандартных отклонения от 1.
Вероятность того, что отличие от среднего
достигнет трех стандартных отклонений
в положительную или отрицательную
сторону, составляет 0,0027. На этом основании
можно сделать два вывода:
-
Нулевая гипотеза верна,
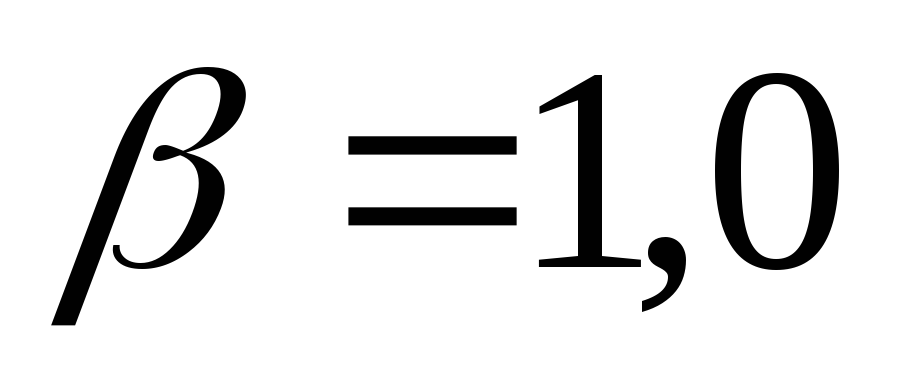 ,
эксперимент дал ложный результат.
Вероятность получения такого исходного
значения имеет место в 0,27% случаев, и
это именно тот случай.
,
эксперимент дал ложный результат.
Вероятность получения такого исходного
значения имеет место в 0,27% случаев, и
это именно тот случай. -
Гипотеза противоречит результату оценивания регрессии. Т.е. принимается альтернативная гипотеза.
Очевидно, что чем меньше вероятность построения регрессии при условии правильности гипотезы, тем больше вероятность отказа от гипотезы и выбора второго вывода.
В большинстве работ
по эконометрике критический уровень
берется 5% или 1%. Если выбирается уровень
5%, то переключение на второй уровень
происходит, когда при истинности нулевой
гипотезы вероятность получения столь
экстремального значения
![]() составляет менее 5%. В этом случае говорят,
что нулевая гипотеза должна быть
отвергнута при 5%-ном уровне значимости.
составляет менее 5%. В этом случае говорят,
что нулевая гипотеза должна быть
отвергнута при 5%-ном уровне значимости.
Это происходит в
тех случаях, когда
![]() отстоит от
отстоит от
![]() более чем на 1,96 стандартного отклонения.
В нормальном распределении это составляет
2,5% в каждую сторону.
более чем на 1,96 стандартного отклонения.
В нормальном распределении это составляет
2,5% в каждую сторону.
Нулевая гипотеза не будет отвергнута, если
-1,96 < z < 1,96,
где z
– число стандартных отклонений между
регрессионной оценкой и гипотетическим
значением
![]() :
:
![]() .
.
Таким образом,
![]() -
-
область принятия
гипотезы для
![]() при 5% уровне значимости.
при 5% уровне значимости.
Аналогично, нулевая гипотеза отвергается при 1% уровне значимости, если
-2,58 < z < 2,58.
Выбор двух уровней обуславливается попыткой найти баланс между риском допущения ошибок I и II рода. Ошибка I рода имеет место в том случае, когда вы отвергаете истинную нулевую гипотезу. Ошибка II рода возникает, когда вы не отвергаете ложную гипотезу.
Таким образом, чем ниже критическая вероятность, тем меньше риск получения ошибок I рода. Но при этом повышается вероятность допущения ошибок II рода.
На практике
стандартное отклонение величины
![]() неизвестно. Тогда вместо исследования
величины z
в примере будем рассматривать t-статистику.
неизвестно. Тогда вместо исследования
величины z
в примере будем рассматривать t-статистику.
![]() ,
здесь
,
здесь
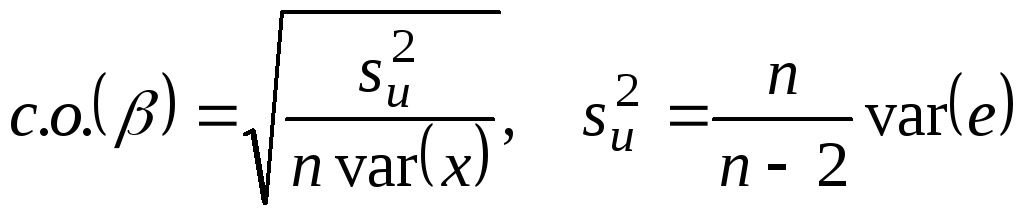 - выборочная дисперсия остатков.
- выборочная дисперсия остатков.
Во-вторых, величина t имеет не нормальное распределение, а распределение Стьюдента или t-распределение. Его точная форма зависит от числа степеней свободы в регрессии, причем с увеличением числа степеней свободы оно приближается к нормальному.
Оценивание каждого параметра в уравнении регрессии поглощает одну степень свободы в выборке. Таким образом, число степеней свободы равно количеству наблюдений в выборке минус количество оцениваемых параметров. Тогда
![]() .
.
Отсюда,
![]() ,
,
т.е. гипотетическое
значение
![]() является совместимым с результатом
оценивания регрессии, если величина
является совместимым с результатом
оценивания регрессии, если величина
![]() удовлетворяет этому неравенству.
Множество всех значений, которые не
опровергаются оценкой
удовлетворяет этому неравенству.
Множество всех значений, которые не
опровергаются оценкой
![]() ,
называются доверительным интервалом.
,
называются доверительным интервалом.
Итак, мы рассмотрели случай, когда альтернативная гипотеза является простым отрицанием нулевой. Исследуем еще три случая:
-
Существует единственное альтернативное истинное значение
 ;
; -
Если
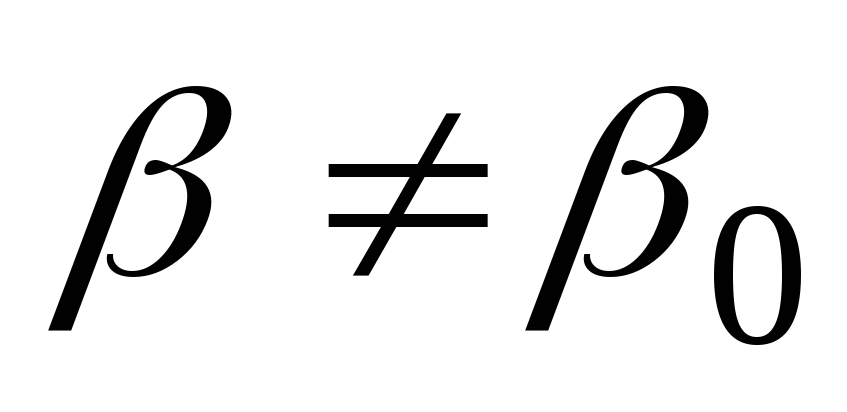 ,
то
,
то
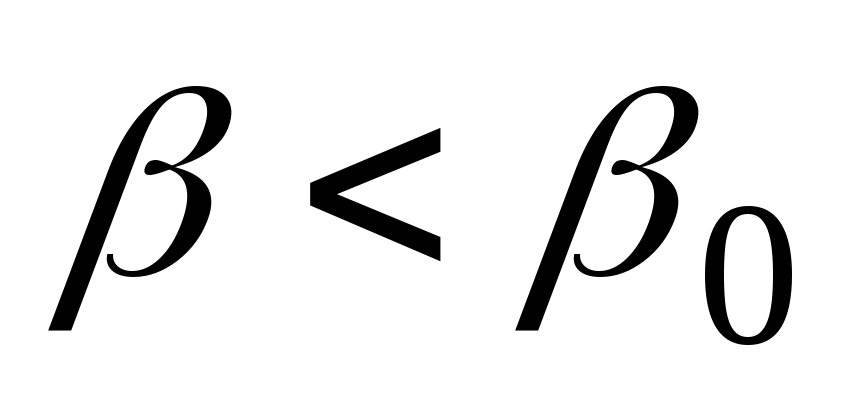 ;
; -
Если
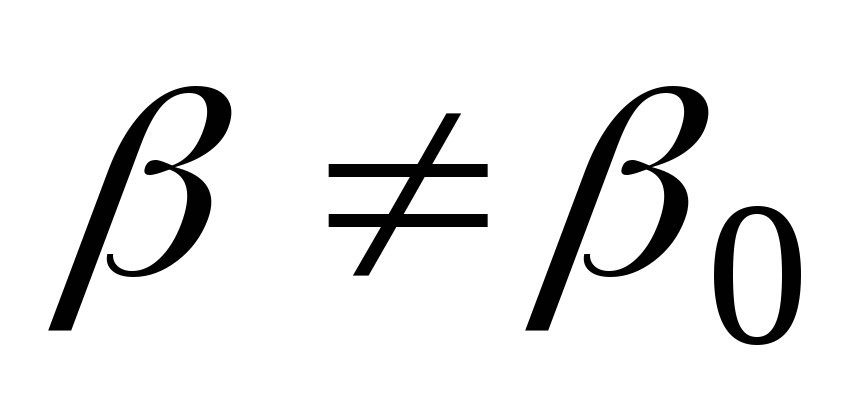 ,
то
,
то
 .
.
-
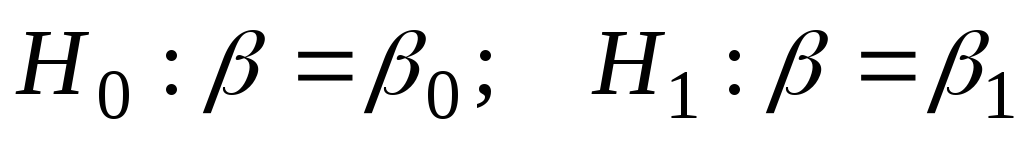 .
.
В A B


![]() и
и
![]() .
Для определенности, допустим
.
Для определенности, допустим
![]() .
Допустим, мы проверяем гипотезу
.
Допустим, мы проверяем гипотезу
![]() при 5%-ном уровне значимости. Найдем
границы для верхней и нижней границы
принятия значения
при 5%-ном уровне значимости. Найдем
границы для верхней и нижней границы
принятия значения
![]() .
Обозначим их через A
и B.
.
Обозначим их через A
и B.
Если
значение
![]() находится справа от B,
то оно лучше совместимо с гипотезой
находится справа от B,
то оно лучше совместимо с гипотезой
![]() .
Если, однако
.
Если, однако
![]() находится слева от A,
то нам все равно необходимо отклонить
нулевую гипотезу и принять
находится слева от A,
то нам все равно необходимо отклонить
нулевую гипотезу и принять
![]() .
Однако, это значение возможно в 2,5%
истинности гипотезы
.
Однако, это значение возможно в 2,5%
истинности гипотезы
![]() ,
и в 0,000…01% случаях гипотезы
,
и в 0,000…01% случаях гипотезы
![]() ,
поэтому логичнее принять все равно
гипотезу
,
поэтому логичнее принять все равно
гипотезу
![]() .
Это означает, что мы принимаем теперь
гипотезу с 2,5% уровнем допущения ошибки.
Т.е. теперь это односторонний критерий.
.
Это означает, что мы принимаем теперь
гипотезу с 2,5% уровнем допущения ошибки.
Т.е. теперь это односторонний критерий.
Аналогично, если
принять
![]() ,
то получим также односторонний критерий,
но в другую сторону.
,
то получим также односторонний критерий,
но в другую сторону.
При рассмотрении второго и третьего случаев достаточно использовать те же односторонние критерии, но отличие заключается в том, что нельзя посчитать мощность критерия.
Проверки с
использованием одностороннего критерия
важны, когда необходимо установить
влияет ли независимая переменная на
зависимую и вместо альтернативной
гипотезы можно сделать предположение
о характере влияния
![]() .
Это является преимуществом, поскольку
критическое значение при проверке
односторонним критерием для отклонения
гипотезы
.
Это является преимуществом, поскольку
критическое значение при проверке
односторонним критерием для отклонения
гипотезы
![]() будет меньшим. А следовательно, это
облегчает отклонение нулевой гипотезы
и установление зависимости.
будет меньшим. А следовательно, это
облегчает отклонение нулевой гипотезы
и установление зависимости.
Однако мощность
критерия можно вычислить лишь в том
случае, если предстоит выбор между
![]() и
и
![]() .
Необходимо вычислить t-статистику
для точки
.
Необходимо вычислить t-статистику
для точки
![]() ,
считая, что
,
считая, что
![]() ,
и использовать таблицу распределения
Стьюдента для нахождения вероятности
того, что
,
и использовать таблицу распределения
Стьюдента для нахождения вероятности
того, что
![]() больше, чем на t
стандартных ошибок, будет стоять слева
от
больше, чем на t
стандартных ошибок, будет стоять слева
от
![]() .
.
Если эту вероятность
обозначить
![]() ,
то мощность критерия составляет
,
то мощность критерия составляет
![]() .
Таким образом, чем выше уровень значимости,
тем больше
.
Таким образом, чем выше уровень значимости,
тем больше
![]() и тем меньше мощность критерия. Используя
односторонний критерий вместо
двустороннего, можно получить большую
мощность при любом уровне значимости.
и тем меньше мощность критерия. Используя
односторонний критерий вместо
двустороннего, можно получить большую
мощность при любом уровне значимости.
