
1.
Будем
рассматривать функции вида U=U(x1,x2,…,xn),
x=(x1,x2,...,xn)
![]() .
.
В частных случаях: при n=2: x1= x; x2= y => U=U(x,y) либо x1= x; x2= t => U=U(x,t); при n=3: x1 = x; x2 = y; x3 = z => U=U(x,y,z) либо x1= x; x2= y; x3= t => U=U(x,y,t); при n=4: x1 = x; x2= y; x3 = z;x4 = t => U=U(x,y,z,t).
В этом случае переменные x, y, z называются пространственными переменными, t - время.
Условимся
для простоты записи обознать частные
производные
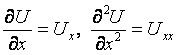 ,
и т.д.
,
и т.д.
Определение. Дифференциальным уравнением с частными производными называется уравнение вида
![]()
Другими словами - это уравнение, связывающее независимые переменные xi, неизвестную функцию U и ее частные производные до порядка k.
Определение. Порядком дифференциального уравнения с частными производными называется высший из порядков частных производных, входящих в это уравнение.
Определение.
Решением уравнения с частными производными
порядка k
называется функция U=U(x1,
x2
, … ,xn),
определенная в некоторой области
![]() ,
которая имеет производные до порядка
k
и
при подстановке в уравнение обращает
его в тождество по (x1,
x2,
… , xn).
,
которая имеет производные до порядка
k
и
при подстановке в уравнение обращает
его в тождество по (x1,
x2,
… , xn).
Определение. Дифференциальное уравнение с частными производными называется линейным, если функция U и ее частные производные входят в него линейным образом.
Запишем общий вид линейного уравнения с двумя переменными: в случае уравнения 1-го порядка:
![]()
(1)
в случае уравнения 2-го порядка:
![]()
(2)
Функции a(x, y), b(x, y), … , A(x, y), B(x, y) … - коэффициенты (заданные функции), f(x, y)- правая часть (заданная функция) линейного дифференциального уравнения.
Определение.
Дифференциальное уравнение с частными
производными называется однородным,
если его правая часть тождественно
равна нулю, т.е
![]() при
всех (x,y)
при
всех (x,y)![]() D.
D.
Определение.
Дифференциальное уравнение с частными
производными называется неоднородными,
если его правая часть тождественно не
равна нулю, т.е.
![]() при
некоторых (x,y)
D.
при
некоторых (x,y)
D.
Определение. Если коэффициенты линейного дифференциального уравнения - постоянные, то такое уравнение называется линейным дифференциальным уравнением с постоянными коэффициентами.
Левая часть уравнения (1) или (2) обычно обозначается через LU и называется линейным дифференциальным оператором с частными производными порядка 1 или 2, соответственно. Тогда линейное неоднородное дифференциальное уравнение будет иметь вид LU = f(x ,y), а линейное однородное дифференциальное уравнение будет иметь вид LU = 0.
Определение.
Выражение вида
![]() или
или
![]() называется
оператором Лапласа, соответственно, на
плоскости или в пространстве.
называется
оператором Лапласа, соответственно, на
плоскости или в пространстве.
Условимся для более краткой записи сокращать (линейное) дифференциальное уравнение до (Л)ДУ, линейное (не)однородное дифференциальное уравнение до ЛОДУ (ЛНДУ).
Среди ЛДУ второго порядка есть уравнения, которые имеют особое значение. Перечислим их:
1. Уравнение Лапласа- уравнение вида ∆U=0 (n=2,3)- ЛОДУ 2-го порядка.
Уравнение Пуассона- уравнение вида ∆U=f (n=2,3)- ЛНДУ 2-го порядка.
2. Волновое уравнение- уравнение вида Utt=a2ΔU, где ΔU=Uxx+Uyy на плоскости или ΔU=Uxx+Uyy+Uzz в пространстве. Одномерное волновое уравнение (на прямой)- уравнение вида Utt=a2Uxx.
3. Уравнение теплопроводности- уравнение вида Ut=a2∆U, где где ΔU=Uxx+Uyy на плоскости или ΔU=Uxx+Uyy+Uzz в пространстве. Одномерное уравнение теплопроводности (на прямой)- уравнение вида Ut =a2Uxx.
Именно эти уравнения являются основными уравнениями математической физики.
олололол ещё одно
Рассмотрим дифференциальное уравнение в частных производных 1го порядка:
![]()
Предположим,
что коэфффициенты Ai (x1
,..,xn )- определены и непрерывны
вместе со своими частными производными
по всем аргументам в окрестности
начальной точки
![]() и
не обращаются одновременно в нуль.
и
не обращаются одновременно в нуль.
Пусть
![]() построим
по уравнению (1) систему о.д.у. в симметричной
форме:
построим
по уравнению (1) систему о.д.у. в симметричной
форме:
![]() В
данной системе все xi
входят равноправно.
В
данной системе все xi
входят равноправно.
Выберем xn в качестве независимой переменной и перепишем систему (2) в нормальной форме:
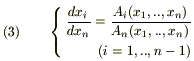
![]()
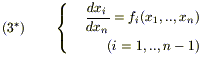
Система (3*) Вам знакома.
Вспомним некоторые понятия и теоремы курса "Обыкновенные диффренциальные уравнения", относящиеся к системам обыкновенных дифференциальных уравнений.
1) Для того, чтобы гарантировать существование хотя бы одного решения системы (3), удовлетворяющие некоторым начальным условиям, достаточно предположить , что правые части системы (3) fi (x1 ,.., xn)- непрерывны в окрестности начальной точки x0 = (x10 ,.., xn0); [ т. Пеано].
2)
Чтобы гарантировать не только
существование, но и единственность
решения задачи Коши для (3), на fi
(![]() )
нужно наложить дополнительные ограничения:
требование существования ограниченных
частных производных от fi
по переменным xi [ т.
Пикара].
)
нужно наложить дополнительные ограничения:
требование существования ограниченных
частных производных от fi
по переменным xi [ т.
Пикара].
В дальнейшем нас будет интересовать именно задача Коши. Поэтому будем считать, что для fi ( ) выполняются условия т.Пикара.
3) При условиях, наложенных на fi ( ) - правые части системы (3), эта система будет иметь ровно (n-1) линейно - независимое решение:
Определение: Совокупность (n-1) функций:
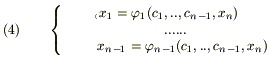 ,
определенных в некоторой области Ω
изменения переменных c1
,.., cn -1 , xn
, непрерывно дифференцируемых относительно
xn, называется общим
решением системы (3). При этом:
,
определенных в некоторой области Ω
изменения переменных c1
,.., cn -1 , xn
, непрерывно дифференцируемых относительно
xn, называется общим
решением системы (3). При этом:
1) система (4) должна быть разрешима в Ω относительно произвольных c1 ,.., cn -1, т.е.
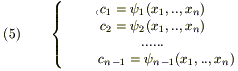 или
или
![]()
2) совокупность (4) является решением системы (2) при всех значениях произвольных постоянных, определяемых формулами (5), когда точка (x1 ,.., xn) пробегает область Ω.
Определение: Функция ψ(x1 ,.., xn), не равная тождественной постоянной, называется интегралом системы (3), если при подстановке в неё какого-либо решения системы (3), получается постоянная.
Определение: Соотношение ψ(x1 ,.., xn) = с, где ψ - интеграл системы (3), с - произвольная постоянная называется первым интегралом системы.
По сути дела и (4), и (5) определяют решения системы (3), при этом (4) - решение в форме Коши.
Определение:
Интегралы ψ1 ,.., ψn
-1 называются независимыми,
если не существует соотношения
![]()
Так как правые части системы (3) определены и дифференцируемы в окрестности Ω точки x0, то эта система имеет ровно (n-1) незвисимых интегралов (первых интегралов). А следовательно и система (2) - имеет (n-1) независимых интегралов.
Определение: Совокупность (n-1) независимых интегралов называется общим интегралом системы (3).
Определение: В пространстве координат x1,..,xn эта система интегралов (5) определяет семейство линий, зависящее от (n-1) параметра, которые называют характеристиками д.у. в ч.пр.(1). Соответственно система (2) называется характеристической системой дифференциальных уравнений для д.у. в ч.пр.(1).
Теорема: Если ψ1 ,.., ψn -1 (x1 ,.., xn) - непрерывно-дифференцируемые интегралы системы (3), то любая непрерывно-дифференцируемая от них функция ψ = F(ψ1 ,.., ψn -1), производные которой по ψ1 ,.., ψn -1 не обращаются в нуль одновременно, также является интегралом системы.
Доказательство:
ψ1 ,.., ψn
-1-интегралы; значит эти интегралы в
силу системы (3) обращаются в постоянную
ψi (x1
,.., xn)(3) = c, т.е.
![]() .
Покажем, что
.
Покажем, что
![]() .
.
![]() -
интеграл системы (3).
-
интеграл системы (3).
Теорема: 1) Если ψ(x1 ,.., xn) есть непрерывно-дифференцируемый интеграл
системы (3), то u = ψ(x1 ,.., xn), является решением уравнения (1).
2)
Если u = u1(x1
,.., xn)![]() const решение уравнения (1), то u1(x1
,.., xn) -
const решение уравнения (1), то u1(x1
,.., xn) -
интеграл системы (3).
Доказательство:
1) так как ψ(x1
,.., xn) интеграл системы
(3), то (при подстановке вместо x1
= φ1( ...,xn ),..,
xn - 1 = φn
- 1( ...,xn ) - решения
системы (3), получим постоянную (по
определению интеграла системы):
ψ[x1(xn
) ,.., xn - 1( xn),
xn] (3) = ψ(xn)
= c ; тогда
![]() .
.
Вычислим полную производную от ψ по xn в силу системы (3):
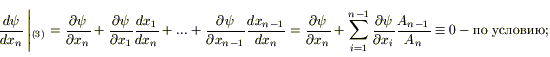
![]() -
в силу системы (3).
-
в силу системы (3).
Домножим последние равенства на Аn.
Получим:
![]()
Доказательство: 2) u1(x1 ,.., xn) const - решение уравнения (1).
Надо
показать, что
![]()
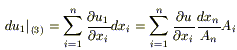 ;
[в силу системы (3)
;
[в силу системы (3)
![]() ].
].
![]() (так
как выражение в скобках - это левая часть
уравнения (1), а u1 - решение
этого уравнения).
(так
как выражение в скобках - это левая часть
уравнения (1), а u1 - решение
этого уравнения).
Следовательно u1(x1 ,.., xn) - интеграл системы (3).
Вывод: задача интегрирования уравнения (1) эквивалентна задаче интегрирования системы (3) (или системы (2)).
Теорема: Если ψ1 ,.., ψn-1 - независимые интегралы системы (3) , то функция u = Φ(ψ1 ,.., ψn -1), где Φ - произвольная функция, является общим решением дифференциального уравнения (1), т.е. решением, содержащим все без исключения решения уравнения (1).
Доказательство: ( от противного ) Пусть существует u = ψ(x1 ,.., xn) - решение уравнения (1); покажем, что ψ не является линейно-независимой, т.е существует функция F, такая, что ψ = F(ψ1 ,.., ψn-1).
Так как ψ1 ,.., ψn -1 - интегралы системы (3), то ψi (i =1 ,.., n-1)- решения уравнения (1). Подставим u = ψ(x1 ,.., xn) и ψi в уравнение(1):
Р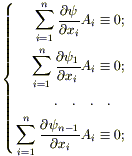 ассмотрим
эту систему, как систему линейных
уравнений относительно Ai
(i =1 ,.., n). Заметим, что в каждой
точке эта система имеет нетривиальное
решение.(так как Ai не
равны нулю одновременно). Отсюда
определитель
системы
должен быть тождественно равен нулю.
ассмотрим
эту систему, как систему линейных
уравнений относительно Ai
(i =1 ,.., n). Заметим, что в каждой
точке эта система имеет нетривиальное
решение.(так как Ai не
равны нулю одновременно). Отсюда
определитель
системы
должен быть тождественно равен нулю.
Этот определитель:
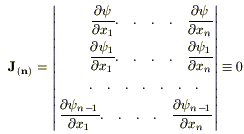 Тождественное
обращение в нуль Якобиана функций
говорит о том, что между ними существует
функциональная зависимость G
(ψ, ψ1 ,.., ψn
-1) = 0; (*)
Тождественное
обращение в нуль Якобиана функций
говорит о том, что между ними существует
функциональная зависимость G
(ψ, ψ1 ,.., ψn
-1) = 0; (*)
В
силу линейной независимости интегралов
ψi(x1
,.., xn) (i =1 ,.., n-1)
существуют по крайней мере один из
миноров (n-1) порядка, отличный от
нуля:
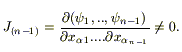
Следовательно (*) можно переписать: ψ = F(ψ1 ,.., ψn-1). Значит ψ не является линейно-независимой по отношению к системе функций ψ1 ,.., ψn -1. Отсюда u = Φ(ψ1 ,.., ψn -1) - действительно содержит все решения уравнения (1).
Вывод: для отыскания общего решения д.у. в ч.пр.(1) необходимо проинтегрировать систему (2) = (3) и записать общее решение
u = Φ(ψ1 ,.., ψn -1), где ψ1 ,.., ψn -1 - интегралы системы (2) = (3).
Геометрически этому решению соответствует семейство интегральных поверхностей.
2 ЗАДАЧА КОШИ
Найти u (x1 ,.., xn), удовлетворяющую дифференциальному уравнению:
которая при фиксированном значении одной из независимых переменных обращается в заданную функцию от остальных переменных.
(6) при xn = xn0 u = H (x1 ,.., xn -1).
Общее решение дифференциального уравнения (1) u = Φ(ψ1 ,.., ψn -1).
Найдем решение уравнения (1), удовлетворяющее н.у.(6). Для этого воспользуемся 1ми интегралами (5) системы (2), положив в них xn = xn0 :
(**)
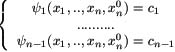 или
или
![]()
Эта система разрешима в окрестности точки (x10 ,.., xn0) относительно x1 ,.., xn -1 :
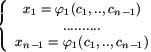
Подставим полученные соотношения xi в начальное условие u = H(x1 ,.., xn -1 ) ( H - известная функция) ; так как u = Φ(ψ1 ,.., ψn -1), то при подстановке (**) получим: u = Φ (c1 ,.., cn -1) = H [ φ1 (c1 ,.., cn -1 ),.., φn -1 (c1 ,.., cn -1) ] ; (где Φ-неизвестная), т.е. мы получили общий вид функции Φ(α1 ,.., αn -1) ; так как общее решение уравнения (1) определяется как Φ(ψ1 ,.., ψn -1), остается вместо сi подставить интегралы ψi :
u ( x1 ,.., xn -1 ) = Φ(ψ 1 ,.., ψn -1) = H [ φ1 (ψ1 ,.., ψn -1 ),..,φn -1 (ψ1 ,.., ψn -1) ]
3
Классификация дифференциальных уравнений с частными производными второго порядка.
Уравнения с частными производными можно классифицировать по разным признакам.
Например:
1. По порядку уравнений: Ut=Uxx (уравнение 2-го порядка), Ut=Ux(уравнение 1-го порядка), Ut=Uxxx + sinx (уравнение третьего порядка).
2.
По числу независимых переменных: Ut=Uxx
(уравнение с 2-мя переменными),
 -
уравнение с тремя переменными.
-
уравнение с тремя переменными.
3. ДУ с частными производными могут быть линейными и нелинейными. Линейные уравнения в свою очередь бывают однородными и неоднородными.
4. ЛДУ 2-го порядка классифицируются по типу: а) Гиперболический тип ( в области D), если выражение δ(x,y)=B2-AC>0 для любых (x, y) D, где A, B, C - коэффициенты в уравнении (2) б) Эллиптический тип (в области D), если выражение δ(x,y)=B2-AC<0 для любых (x,y) D в) Параболический тип (в области D), если выражение δ(x,y)=B2-AC = 0 для любых (x,y) D.
Отметим, что тип уравнения определяется только коэффициентами A,B,C при производных 2-го порядка. При невырожденной замене переменных тип не меняется.
г) Смешанный тип, если в области D уравнение имеет разный тип в разных точках.
Пример. Рассмотрим уравнение
yUxx + Uyy = 0
Оно возникает в газовой динамике и называется уравнением Трикоми. Для этого уравнения выражение δ(x,y) = B2 - AC = -y. Тогда при y>0 выражение δ(x,y)<0 и уравнение имеет эллиптический тип. При y<0 выражение δ(x,y)>0, следовательно, уравнение гиперболического типа, а при y=0, соответсвенно, δ(x,y)=0 и уравнение имеет параболический тип (см. рис. 1)

Рис. 1
Замечания. 1. Уравнения с постоянными коэффициентами имеют один тип на всей области определения. Так, например, волновое уравнение на плоскости и в пространстве имеет гиперболический тип, уравнение теплопроводности на плоскости и в пространстве - параболический тип, а уравнение Лапласа - эллиптический тип. 2. Классификация ЛДУ с большим числом переменных почти аналогична.
Оололол ещё
Большая часть всех уравнений в частных производных 2го порядка, линейных относительно вторых производных являются представителями 3х различных классов уравнений, которые существенно отличаются друг от друга по методам исследования и по физической природе (описывают различные физические явления).
Остановимся более подробно на случае 2х независимых переменных: u = u(x,y).
![]()
a,b,c - функции, определенные в некоторой области Ω = Oxy и имеющие непрерывные производные до 2го порядка.
f - непрерывная функция своих аргументов; если f - линейная относительно u, ux , uy, то уравнение (1) - линейное.
Поставим перед собой задачу: с помощью замены независимых переменных (x, y) привести уравнение (1) к наиболее простому виду.
Введем
новые переменные:
![]() ,
и потребуем, чтобы они были
дважды непрерывно-дифференцируемы и
чтобы якобиан перехода:
,
и потребуем, чтобы они были
дважды непрерывно-дифференцируемы и
чтобы якобиан перехода:
![]() в
области Ω.
в
области Ω.
Преобразуем производные к новым переменным:
![]()
![]()
![]()
![]()
Тогда уравнение (1) в новых переменных примет вид:
![]()
где

Попытаемся выбрать ξ(x, y) и η(x, y) так, чтобы обратить в нуль некоторые из коэффициентов A,B,C.
Вопрос об обращении A и С в нуль эквивалентен вопросу о разрешимости дифференциального уравнения 1го порядка.
![]() относительно
неизвестной функции z(x,
y).
Поделим на zy2:
относительно
неизвестной функции z(x,
y).
Поделим на zy2:
![]()
Решим
как квадратное уравнение относительно
![]() :
:

Решая каждое из них методом характаристик:


![]() -
интегралы системы (*), а, следовательно,
решения уравнения (4).
-
интегралы системы (*), а, следовательно,
решения уравнения (4).
Уравнения (5) могут быть записаны в виде одного уравнения:
![]()
Обычно
это уравнение и используют для определения
интегралов системы (5). Поведение функций
φ(x,
y)
и ψ(x,
y),
а, следовательно, и искомый простейший
вид исходного уравнения зависит от
знака
![]()
Определение:
Уравнение (1) называется в некоторой
точке
![]()
гиперболического типа, если

эллиптического типа, если
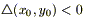
параболического типа, если
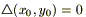
Определение:
Если знак
![]() сохраняет
знак, или
сохраняет
знак, или
![]() в
некоторой области
в
некоторой области
![]() ,
то уравнение является гиперболическим,
эллиптическим или параболическим в
области G1:
,
то уравнение является гиперболическим,
эллиптическим или параболическим в
области G1:
Пример:

![]()
![]()
![]()
4
Канонический вид ЛДУ 2-го порядка с частными производными (n=2).
Можно показать, что:
![]()
Рассмотрим три случая:
1)
![]() -
уравнение гиперболического типа.
-
уравнение гиперболического типа.
В этом случае уравнения (5) и их общие интегралы вещественны и различны: . Они определяют два вещественных и различных семейства характеристик.
Положим:
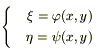
Тогда из
получаем,
что A = C = 0; из
получаем,
что
![]()
Поделим уравнение на 2B, получим:
![]()
Это первая каноническая форма уравнения гиперболического типа.
С
помощью замены
![]() уравнение
(8) можно привести к виду:
уравнение
(8) можно привести к виду:
![]()
Это вторая каноническая форма уравнения гиперболического типа.
2)
![]() -
уравнение параболического типа.
-
уравнение параболического типа.
Уравнения (5), а следовательно, и их интегралы совпадают, т.е. мы получаем только одно вещественное семейство характристик:
![]() -
имеем одно решение; соответственно
имеем ξ = φ(x, y).
-
имеем одно решение; соответственно
имеем ξ = φ(x, y).
В качестве второй переменной η(x, y) возьмем любую дважды непрерывно-дифференцируемую функцию, для которой:
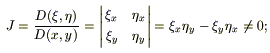
Тогда
из (3) имеем
![]() ;
так как
;
так как
![]()
Покажем,
что
![]() так
как
так
как
![]()
![]()
Если
С = 0 в точке M0, то aηx
+ bηy = 0; добавим уравнение,
определяющее семейство характеристик:
aξx + bξy
= 0; тогда
![]()
Рассматривая эту систему, как систему линейных алгебраических уравнений относительно а и b. Так как а и b не обращаются в нуль одновременно, то у системы существует нетривиальное решение. Следовательно D = 0, так как D = J, то J = 0.
![]() ,
что противоречит (*). Значит
.
Поделим (2) на С:
,
что противоречит (*). Значит
.
Поделим (2) на С:
![]()
Это каноническая форма уравнения параболического типа.
3)
![]() .
Коэффициенты уравнений (5), а следовательно
и 1ые интегралы уравнений -
комплексные величины.
.
Коэффициенты уравнений (5), а следовательно
и 1ые интегралы уравнений -
комплексные величины.
Пусть
![]() -
один из интегралов (5), тогда другой
интеграл будет комплексно сопряженным
с указанным.
-
один из интегралов (5), тогда другой
интеграл будет комплексно сопряженным
с указанным.
![]()
![]()
Чтобы
не иметь дела с комплексными переменными,
введем новые переменные
![]()
![]()
так как ξ = φ(x, y) - интеграл уравнения (5), отсюда - решением уравнения (4).
Разделим в этом тождестве действительные и мнимые части:
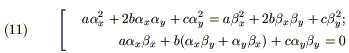
Из
(3) и (11) ![]() [где через
[где через
![]() обозначены
идентичные A, B, C функции из (3), только
при новой (α,β) замене].
обозначены
идентичные A, B, C функции из (3), только
при новой (α,β) замене].
Из
(7) ![]()
Поделим уравнение (2) на А:
![]()
Т.е. для уравнения эллиптического типа после определения 1ых интегралов системы (5) достаточно положить:
![]()
Примеры
![]()
![]() уравнение
параболического типа всюду:
уравнение
параболического типа всюду:
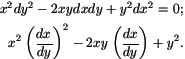
![]()
![]()
Пусть ( η = y ).
![]()
так как уравнение параболического типа, то A = 0; B = 0;
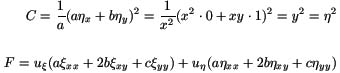
![]()
![]()
![]()
![]()
Дважды интегрируем по переменной η:
![]()
![]()
Возвращаясь
к исходным переменным, получим общее
решение:
![]()
6
Изучение методов построения решений краевых задач для уравнений гиперболического типа мы начинаем с задачи с начальными условиями для неограниченной струны (задача Коши).
(1)
utt - a2 uxx
= 0,
![]() .
.
(2)
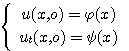 ,
t > 0.
,
t > 0.
Преобразуем это уравнение к каноническому виду, содержащему смешанную производную.
Уравнение характеристик: dx2 - a2 dt2 = 0 распадается на два уравнения: dx - adt = 0 , dx + adt = 0
интегралами которых являются прямые x - at = c1, x + at = c2.
Вводим, как обычно новые переменные: ξ = x + at, η = x - at. Уравнение колебаний струны преобразуем к виду:
(3) uξ η = 0
Проинтегрируем (3) по переменной ξ :
![]()
![]()
Проинтегрируем полученное равенство по η и получим:
![]()
Итак общее решение дифференциального уравнения (3) может быть записано:
u(ξ, η) = F(ξ) + G(η)
Возвращаясь к исходным переменным (x,t), получаем:
(4) u(x,t) = F(x + at) + G(x - at)
Определим функции F и G таким образом, чтобы удовлетворялись начальные условия. Для этого подставим общее решение в начальные условия (2):

Интегрируя второе равенство, получим:
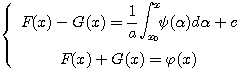
Из полученных равенств находим:
(5)
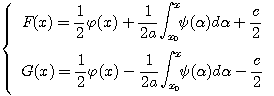
Таким образом, мы определили функции F и G через заданные функции φ и ψ . Подставляя в (4) найденные значения получим:
u(x,t) = F(x + at) + G(x - at)
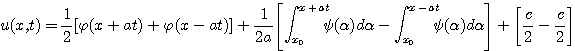
(6)
![]()
Формула (6) называется формулой Даламбера.
Она определяет решение задачи Коши для волнового уравнения.
Замечание.
Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.
. Теорема единственности
Решение краевых задач математической физики сводится к отысканию функции, удовлетворяющей данному уравнению и дополнительным начальным и краевым (граничным) условиям. При этом требуется, чтобы:
1) дополнительные условия были достаточны для выделения единственного решения;
2) среди дополнительных условий не было бы несовместимых.
Первое достигается доказательством теоремы единственности, второе - непосредственным нахождением решения или доказательством теоремы существования.
В качестве примера рассмотрим теорему единственности для уравнения
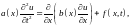 (1)
(1)
где
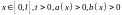 .
Начальные условия
.
Начальные условия
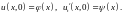 (2)
(2)
В качестве
граничных условий при
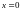 рассмотрим любое из трех следующих:
рассмотрим любое из трех следующих:
1) граничное условие первого рода (заданный режим)
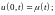 (3)
(3)
2) граничное условие второго рода (заданная сила)
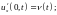 (4)
(4)
3) граничное условие третьего рода (упругое закрепление)
 (5)
(5)
При
 граничные условия задаются аналогично.
граничные условия задаются аналогично.
Комбинируя (3) - (5), получаем шесть типов простейших граничных условий.
Теорема (единственности). Пусть
в уравнении (1) коэффициенты
 и
и
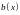 непрерывны на
непрерывны на
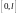 ,
а функции
,
а функции
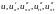 непрерывны при
непрерывны при
 и
и
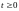 .
Тогда решение уравнения (1), удовлетворяющее
начальным условиям (2) и граничным
условиям
.
Тогда решение уравнения (1), удовлетворяющее
начальным условиям (2) и граничным
условиям
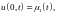
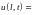
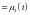 ,
единственно.
,
единственно.
Доказательство. Допустим, что
существуют два решения
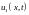 и
и
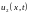 .
Легко проверить, что разность
.
Легко проверить, что разность
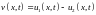 удовлетворяет однородному уравнению
удовлетворяет однородному уравнению
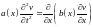 и однородным начальным и граничным
условиям
и однородным начальным и граничным
условиям
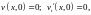 (6)
(6)
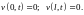 (7)
(7)
Докажем, что
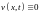 .
.
Рассмотрим функцию
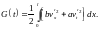 Дифференцируя по
Дифференцируя по
 ,
получим
,
получим
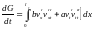 .
Проинтегрируем по частям первое
слагаемое:
.
Проинтегрируем по частям первое
слагаемое:
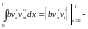
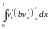 .
Из граничных условий (7) следует, что
.
Из граничных условий (7) следует, что
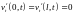 .
Поэтому внеинтегральное слагаемое
равно нулю и
.
Поэтому внеинтегральное слагаемое
равно нулю и
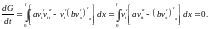
Отсюда и из начальных условий (5) следует, что
 (8)
(8)
Наконец,
учитывая, что коэффициенты
 и
и
 положительны, заключаем, что подынтегральное
выражение в (8) тождественно равно нулю.
Поэтому
положительны, заключаем, что подынтегральное
выражение в (8) тождественно равно нулю.
Поэтому
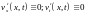 и
и
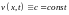 .
Из начальных условий (6)
.
Из начальных условий (6)
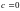 ,
что приводит к тождеству
,
что приводит к тождеству
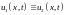 .■
.■
Задача. Для уравнения (1) доказать теоремы единственности при граничных условиях второго рода (4) и третьего рода (5).
7
Попробуем решить задачу Коши для неоднородного волнового уравнения с однородными начальными условиями:
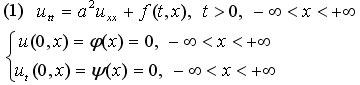
Для того чтобы решить задачу (1) для функции u(t,x) найдем сначала решения вспомогательной задачи

Решение этой задачи можно найти, используя формулу Даламбера с введение новой переменной:
![]()
Получаем:
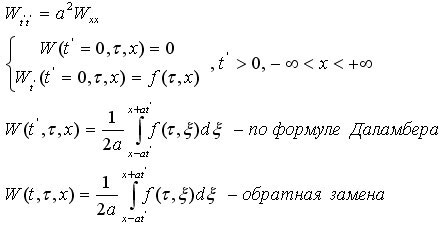
Искомое решение задачи (1) будет иметь вид:
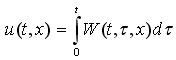
Дифференцируем по переменной t
Для этого надо вспомнить формулу:
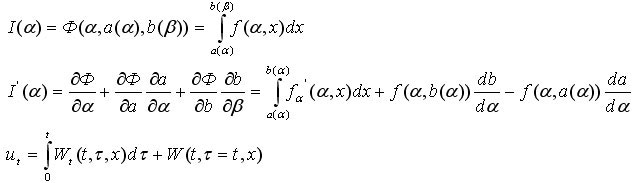
Используя первое начальное условие вспомогательной задачи, получим:
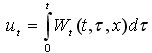
Дифференцируем по t еще раз:

Воспользуемся вторым начальным условием вспомогательной задачи для W:
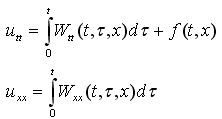
Подставим в уравнение (1) и получим:
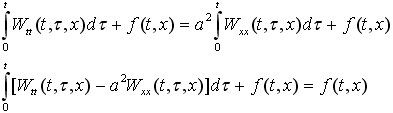
Так как W-решение вспомогательной задачи

Изучение методов построения решений краевых задач для уравнений гиперболического типа мы начинаем с задачи с начальными условиями для неограниченной струны (задача Коши).
(1) utt - a2 uxx = 0, .
(2) , t > 0.
Преобразуем это уравнение к каноническому виду, содержащему смешанную производную.
Уравнение характеристик: dx2 - a2 dt2 = 0 распадается на два уравнения: dx - adt = 0 , dx + adt = 0
интегралами которых являются прямые x - at = c1, x + at = c2.
Вводим, как обычно новые переменные: ξ = x + at, η = x - at. Уравнение колебаний струны преобразуем к виду:
(3) uξ η = 0
Проинтегрируем (3) по переменной ξ :
Проинтегрируем полученное равенство по η и получим:
Итак общее решение дифференциального уравнения (3) может быть записано:
u(ξ, η) = F(ξ) + G(η)
Возвращаясь к исходным переменным (x,t), получаем:
(4) u(x,t) = F(x + at) + G(x - at)
Определим функции F и G таким образом, чтобы удовлетворялись начальные условия. Для этого подставим общее решение в начальные условия (2):
Интегрируя второе равенство, получим:
Из полученных равенств находим:
(5)
Таким образом, мы определили функции F и G через заданные функции φ и ψ . Подставляя в (4) найденные значения получим:
u(x,t) = F(x + at) + G(x - at)
(6)
Формула (6) называется формулой Даламбера.
Она определяет решение задачи Коши для волнового уравнения.
