Теорема единственности 1ой краевой задачи

Понятие решения 1^ой краевой задачи

Решением 1^ой краевой задачи для уравнения теплопроводности будем называть функцию u(x,t), обладающую следующими свойствами:

1. u(x,t) определена и непрерывна в замкнутой области   ;

2. u(x,t) удовлетворяет уравнению теплопроводности в открытой области, т.е. 0<x₀<l ;   t > t₀;

3. u(x,t) удовлетворяет начальному и граничному условиям, т.е. u(x,t₀) = φ(x);   u(0,t) = μ₁(t);   u(l ,t) = μ₂(t);

где φ(x), μ₁(t), μ₂(t) - непрерывные функции, удовлетворяющие условию сопряжения: φ(0) = μ₁(t₀);   φ(l ) = μ₂(t₀)   (необходимы для непрерывности функции u(x,t) в замкнутой области).

  - плоскость фазовых состояний (x,t).

В нашей задаче ищется функция u(x,t), определенная внутри прямоугольника ABCD. Эта область определяется самой постановкой задачи, так как изучается процесс распределения тепла в стержне за промежуток времени , в течение которого нам известен тепловой режим на границах.

Замечание:   требуем, чтобы уравнение удовлетворяло для u(x,t) в открытой области, т.е. не при t = 0, x = 0 и x = l. Если бы уравнение удовлетворяло при t = 0, то должны потребовать существование φ'' = u_xx(0,x) - входит в уравнение . Это требование ограничивает область изучаемых физических явлений, так как исключили бы те функции φ(х), для которых это условие не выполняется.

Непрерывность u(x,t) при следует из того, что u(x,t) удовлетворяет уравнению, т.е. требование непрерывности функции в замкнутой области относится по сути дела только к тем точкам, где задаются начальные и граничные условия.

В дальнейшем под словами "решение уравнения, удовлетворяющее граничным условиям" будем подразумевать функцию, удовлетворяющую требованиям 1), 2), 3).

Теорема:  если две функции u₁(x,t) и u₁(x,t), определены и непрерывны в Ĝ, удовлетворяющие уравнению теплопроводности:   u_x = a² u_xx + f(x,t) в G, одинаковым начальным и граничным условиям:

  u₁(x,0) = u₂(x,0) = φ(x);

  u₁(0,t) = u₂(0,t) = μ₁(t);

  u₁(l ,t) = u₂(l ,t) = μ₂(t),

то

Доказательство:   рассмотрим   υ(x,t) = u₂(х ,t) - u₁(х ,t)

Так как для функции υ(x,t) - однородное уравнение (f(x,t) = 0), то для нее одновременно выполняются max и min, т.е. max и min достигаются при t = 0: x = 0 или x = l;  υ(x,0) = 0;  υ(0,t) = 0;  υ(l ,t) = 0, , т.е. .

Теорема:  пусть u₁ и u₂ - решения уравнения (*) при различных условиях на границе Г: u_i /_Г = ψu(x,t), i = 1,2, причем   .

Тогда всюду в Ĝ будет выполняться неравенство   .

Доказательство:   разность решений υ = u₂ - u₁ - удовлетворяет однородному уравнению (*) и условию на Г: .

Применим к функции υ(x,t) следствие3 из принципа максимального значения. Получим, что в Ĝ, тогда   в Ĝ.

Теорема: (единственности для бесконечной прямой) 

При доказательстве этой теоремы существенно требование ограниченности искомой функции во всей области, т.е. мы будем предполагать: существует М такое, что /u(x,t)/ < M для всех .

Теорема:  если u₁ и u₂ - непрерывные, ограниченные во всей области изменения переменных (x,t) функции, удовлетворяющие уравнению теплопроводности:   u_x = a² u_xx, и условию: u₁(х,0) = u₂(х,0)   ( ), то для .

Доказательство:   рассмотрим функцию υ(x,t) = u₁(х ,t) - u₂(х ,t);   υ(x,t) - удовлетворяет уравнению теплопроводности; непрерывна и ограничена:

  ; υ(x,0) = 0.

Принцип максимума неприменим, так как в неограниченной области функция может нигде не достигать своего максимального значения.

Рассмотрим область , где L - вспомагательное число и функцию - непрерывна, удовлетворяет уравнению теплопроводности и обладает свойствами (оценка функций на границе Г):

  ;

  .

т.е. на границе

Для ограниченной области справедлив принцип максимума. Применим следствие2 к функциям:

  ů = - w(x,t);  u = υ(x,t);   ũ = w(x,t);

 

фиксируем (x,t); переходим к пределу при . Получим: , следовательно . Значит u₁(х ,t)  u₂(х ,t)

24

Рассмотрим задачу Коши для уравнения теплопроводности:

(3)  

Считаем, что u(x,t) и φ(x) функции для которых существует интеграл Фурье.

Обозначим   U(λ ,t) = R [u];   Ф(λ) = R [φ]

Шаг 1:   Применяем преобразование Фурье к нашей задаче.В силу свойства линейности можем применить к левой и правой части уравнения и начальные условия:  

(4)

Шаг 2:   Решаем новую задачу в образах: λ входит как параметр, в уравнении производных по λ нет (только по t);

его решение:   . Используя начальное условие, определяем С: U(λ ,0) = С = Ф(λ).

Окончательно: , т.е. U(λ ,t) = Ф(λ) G(λ) = R [φ(x)] R [g(x,t)] = R(φ g).

Функция   φ(x) - известна. Надо найти g(x,t) - оригинал функции G(λ).

Воспользуемся табличными значениями: .

Шаг 3:  

В последнем равенстве выяснено, что из себя представляет "табличный" коэффициент λ в нашей задаче:

;   .

Мы нашли функцию g(x,t). Осталось по определению записать свертку функций φ и g(x,t).

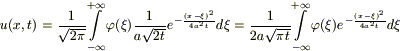
(5) 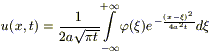 - формула Пуассона.

Функция   - является фундаментальным решением уравнения теплопроводности.

G*  называется функцией влияния мгновенного точечного источника.

G* (x ,ξ ,t) - представляет температуру стержня в точке х в момент времени t, вызванная действием мгновенного точечного источника мощности Q = cp, помещенного в момент t = 0 в точку x = ξ. Тогда u(x,t) - можем рассматривать как результат суперпозиции температур, возникающих в точке х в момент времени t вследствие непрерывно распределенных по стержню тепловых источников "интенсивности" φ(х)cp  в точке λ, приложенных в момент времени t = 0.

Покажем, что формула Пуассона для любой ограниченной функции /φ(λ)/<M представляет при t>0 U(x,t) ограниченное решение уравнения теплопроводности, u(x,t) непрерывно примыкающее при t = 0 к φ(х) во всех точках непрерывности этой функции.