8.7. Кинетика реакций при конечных степенях заполнения поверхности

В предыдущих разделах кинетика электродных реакций рассмотрена в приближений изотермы Генри. Однако, если допустить, что степень заполнения поверхности реагирующими частицами не бесконечно мала, то для вывода кинетического уравнения вместо изотермы Генри следует воспользоваться какой-нибудь другой адсорбционной изотермой, например, Ленгмюра, М. И. Темкина, Конвея-Гилеади, А. Н. Фрумкина, Б. Б. Дамаскина — Б. Н.Афанасьева и др. Как показали Бокрис и Парсонс, возможности, которые создаются для вывода кинетических уравнений, благодаря учету адсорбционных явлений весьма разнообразны и обусловлены тем, что может происходить адсорбция одного или нескольких промежуточных продуктов реакции, их взаимодействие с поверхностью электрода, другими компонентами реакции, а также составляющими электролита.

Рассмотрим лишь простейшие случаи учета адсорбции промежуточных продуктов многостадийной электрохимической реакции на примере реакции разряда — ионизации на кобальтовом электроде.

Допустим, что механизм реакции определяется по Я. Д. Зытнеру нижеследующей последовательностью стадий с образованием промежуточного двухъядерного гидроксокомплекса кобальта:

1. Со²⁺ + ОН^– = СоОН⁺

2. СоОН⁺ + е = СоОН

3. СоОН + Со²⁺ = Co₂OH²⁺

4. Со₂ОН²⁺ + е = Со₂ОН⁺

5. Co₂OH⁺ + е = Со₂ОН (лимитирующая стадия)

6. Со₂ОН + е = 2Co + OH^–

_______________________

2Co²⁺ + 4e = 2Co

Предположим, что замедленной стадией является стадия присоединения третьего электрона в катодном процессе и отщепления второго электрона в анодном процессе. Рассмотрим сначала случай, когда адсорбция частиц в замедленной стадии реакции мала и подчиняется изотерме Генри. Тогда скорость катодной реакции

(θ — степень заполнения поверхности частицами Со₂ОН⁺). Поскольку предшествующие стадии квазиравновесны, то потенциал катода будет одновременно равновесным потенциалом предшествующих электрохимических стадий:

;

Кроме того, для химических стадий должны быть справедливы выражения констант равновесия:

и

Определив из этих уравнений и подставив ее в уравнение скорости катодной реакции, получим:

где К_к = K_к’K₄K₃K₂K₁.

Аналогично для скорости анодной реакции

(θ₁ — степень заполнения поверхности частицами Со₂ОН).

Для предшествующей квазиравновесной электрохимической стадии:

Отсюда окончательно получаем:

где K_a = K_a’K₆.

Из уравнений для скоростей катодного и анодного процессов следует, что в пределах применимости изотермы Генри тафелевские полулогарифмики во всем интервале потенциалов имеют постоянные углы наклона, которые, например, в рассмотренном случае равны:

;

Для комнатной температуры и коэффициентов переноса замедленной стадии α_k = α_a = 0,5 угловые коэффициенты тафелевских прямых равны соответственно 0,024 и 0,04 В.

Равным образом неизменяемы и порядки катодной и анодной реакций по активностям ионов, принимающих участие в реакции, во всем диапазоне изменения концентраций.

Рассмотрим теперь случай, когда степень заполнения поверхности частицами, участвующими в замедленной стадии, конечна и подчиняется изотерме адсорбции Ленгмюра. Для этого случая кинетические уравнения записываем в виде:

;

Здесь коэффициенты переноса α_k и α_а относятся к реакции замедленной стадии.

Для дальнейшего вывода примем, что: 1) поверхность электрода энергетически однородна; 2) на каждом активном месте может адсорбироваться лишь одна частица и 3) силами взаимодействия между адсорбированными частицами можно пренебречь. Эти допущения вводятся при выводе изотермы адсорбции Ленгмюра. Стадия, предшествующая замедленной, является квазиравновесной. В прямом направлении она протекает на свободной доле поверхности (1 – θ – θ₁), а в обратном — на доле поверхности, занятой частицами Со₂ОН⁺ (θ). Для этой стадии должно соблюдаться равенство скоростей прямой и обратной реакций, т. е.

Отсюда уравнение Ленгмюра принимает вид

поскольку α_4k и α_4a относятся к одной и той же одноэлектронной электрохимической реакции и, следовательно, их сумма равна единице. Более ранние стадии катодного процесса также квазиравновесны и их участники адсорбируются незначительно. Поэтому для них воспользуемся константами равновесия и равновесным потенциалом, приведенными выше. Подставим из этих уравнений активность промежуточного продукта в уравнение изотермы адсорбции

(здесь К* = (К_4прям/К_4обр) K₃K₂K₁ и определим θ

или

В уравнение входит переменная величина θ₁, которая может быть определена из аналогичных рассуждений для анодного процесса.

В анодном процессе стадия, предшествующая замедленной, квазиравновесна. В прямом направлении она протекает на доле поверхности θ₁, занятой веществом Со₂ОН, а в обратном – на свободной поверхности (1 – θ – θ₁). Таким образом

и уравнение Ленгмюра примет вид:

Решаем данное уравнение относительно θ₁

Подставив выражение для θ₁ в уравнение для θ

окончательно приходим к формуле:

Подставив выражение для θ в формулу для θ₁, аналогичным образом получаем окончательное выражение для θ₁:

С помощью равенства для θ кинетическое уравнение катодного процесса записываем в виде:

В общем случае это уравнение не дает прямолинейную тафелевскую полулогарифмику. Однако для двух предельных случаев такие полулогарифмики получаются. При небольших смещениях потенциала в катодную сторону (Е < 0), когда

;

т. е. получается уравнение, идентичное уравнению катодного процесса при справедливости изотермы адсорбции Генри.

С другой стороны, когда потенциал значительно сдвинут в катодную сторону и

выражение для плотности тока принимает вид:

Промежуточная область поляризационной кривой в полулогариф-мических координатах не прямолинейна.

Уравнение для анодной поляризационной кривой получается подстановкой выражения для θ₁ в кинетическое уравнение анодного процесса:

Это уравнение также не дает тафелевской полулогарифмики. Но для предельных случаев, когда при небольших анодных поляризациях (Е > 0)

или в случае больших анодных поляризаций, когда

получаются уравнения

и

дающие тафелевские полулогарифмики. Как и в случае катодного процесса, при этих допущениях получаются уравнения, аналогичные уравнениям, выведенным выше для малых θ и θ₁.

Поляризационные кривые, отвечающие рассмотренной схеме, представлены на рис. 8.14. Экстраполяция до пересечения тафе-левских катодных и анодных участков, полученных при малых

Рис. 8.14. Схема катодных и анодных поляризационных кривых для случая адсорбции промежуточных частиц в соответствии с изотермой адсорбции Ленгмюра.

Значения б отвечают предельным случаям малых и больших заполнений при α_к = α_а = 0,5 и комнатной температуре. Прямые 1 — 3 и 1' — 3' соответствуют разным активностям ОН^–.

Рис. 8.15. Схема катодной и анодной поляризационных кривых для случая адсорбции промежуточных частиц в соответствии с изотермой Темкина.

плотностях тока, дает значение равновесного потенциала. В том, что это действительно равновесный потенциал, легко убедиться, приравнивая друг другу правые части уравнений для i_k и i_a:

Решение этого уравнения относительно Е_р дает

т. е. формулу Нернста для кобальтового электрода.

Допустим теперь, что поверхность твердого электрода энергетически неоднородна, т. е. энергия адсорбции на разных участках различна. Имеется целый спектр значений энергии адсорбции от максимальной, отвечающей наиболее активным точкам поверхности, до минимальной — на наименее активных местах. Естественно, что при адсорбции в первую очередь заполняются наиболее активные участки поверхности, а при десорбции сначала освобождаются участки с наименьшей энергией адсорбции. Эффект неоднородности поверхности, согласно М. И. Темкину, сказывается через энергию активации. Энергия активации электрохимической реакции с увеличением степени заполнения меняется на некоторую долю энергии адсорбции. Вследствие этого энергия активации изменяется со степенью заполнения поверхности частицами, участвующими в электрохимической реакции.

Для прямой реакции

где f(θ) — какая-то функция степени заполнения, вид которой нужно задать; δ — коэффициент, изменяющийся в пределах от нуля до единицы.

Для обратной реакции:

Вид функции f(θ) может быть различным. Если принять, что f(θ) линейно изменяется с потенциалом

f(θ) = const + FE

то кинетические уравнения примут вид:

и

Ранее значения степеней заполнения θ и θ₁ были определены из равенства скоростей быстрых прямых и обратных предшествующих стадий, для которых энергии активации малы и их изменением от степени заполнения можно пренебречь. Поэтому выражения для θ и θ₁ можно принять такими же, как и в приближении изотермы Ленгмюра. Тогда

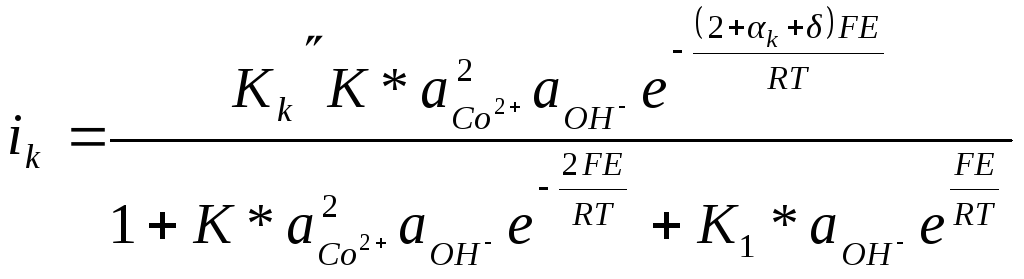
и

Дальнейший ход рассуждений совершенно аналогичен приведенному выше. Для предельных случаев малых и больших плотностей тока соответственно получаем:

;

;

Из уравнений для малых плотностей тока при Е = Е_р получается формула Нернста, а ход потенциала от lg i представлен на рис. 8.15. Значение δ принято равным 0,5. Отличие от случая однородной поверхности проявляется в величинах тафелевских констант b и появлении предельного тока на анодной поляризационной кривой. При значениях δ, отличных от 0,5, предельный ток исчезает и углы наклона несколько изменяются.