8.2.1. Уравнение поляризационной кривой без учета специфической адсорбции и ψ’-потенциала

Плотность тока, протекающего через электрод (регистрируемая прибором), всегда равна разности частных плотностей токов: i = i₂ – i₁. При равновесном потенциале измеряемый ток равен нулю и i₁ = i₂ Значение частных плотностей токов при равновесном потенциале называется плотностью тока обмена i₀. Следовательно, если потенциал электрода равен равновесному (Е = Е_p), можно записать: i_l = i₂ = i₀ или, воспользовавшись последними уравнениями разд. 8.2:

При сдвиге потенциала от равновесного значения через электрод начинает протекать ток, равный разности

Умножим и разделим правую часть уравнения на i₀, причем в каждом из членов разности в знаменателе i₀ заменим на соответствующие члены предыдущего уравнения:

и

и

Из этого уравнения, называемого полным уравнением поляризационной кривой, следует, что при сдвиге потенциала от равновесного значения в катодную сторону (Е < Е_р) i = i_K < 0, а при сдвиге в анодную сторону (Е > Е_р) i = i_a > 0. Таким образом, при указанной системе записи плотности тока i = i₂ – i₁ мы уславливаемся считать катодный ток отрицательным, а анодный положительным. Равноценна и противоположная система записи (i = i₁ – i₂), но мы ею не будем пользоваться.

Соотношения между полной поляризационной кривой и частными поляризационными кривыми показаны на рис. 8.7.

При достаточно высоких катодных или анодных перенапряжениях измеряемый ток очень близок к i_к или i_а. Это связано с тем, что при увеличении перенапряжения один из экспоненциальных членов в последнем уравнении стремится к нулю. При потенциалах электрода, близких к равновесному, нельзя пренебречь ни одной из составляющих. В этом случае η << RT/zF и экспоненты в правой части уравнения можно разложить в ряд. Ограничиваясь двумя первыми членами ряда (е^x = 1 + х и е^–x = 1 – х), получим:

Так как α_а + α_к = 1, то

Это уравнение называется полным уравнением поляризационной кривой при малых перенапряжениях. В координатах плотность тока — перенапряжение онопредставляет прямую линию с наклоном i₀(zF/RT), проходящую через начало координат, причем значение плотности тока не зависит от коэффициентов переноса. Область перенапряжений, в которой экспериментально реализуется линейная зависимость, невелика и, например, при отклонениях от линейности в

Рис. 8.7. Зависимость плотности тока от перенапряжения при α_к = α_а = 0,5.

1% составляет 0,013/z В, если α = 0,5. При уменьшении α область линейности резко сокращается и, когда α = 0,4, равна 0,0026/z В. Из наклона прямой di/dη = i₀(zF/RT) при малых поляризациях определяется ток обмена, а обратная величина dη/di, при η → 0 равная

получила название сопротивления переноса заряда постоянному току.

При высоких перенапряжениях, когда η >> (RT/zF) , один из членов разности в уравнении полной поляризационной кривой уменьшается, а другой — возрастает настолько, что уменьшившимся членом можно пренебречь. При катодном процессе, по условию, перенапряжение имеет отрицательный знак, при анодном — положительный. В соответствии с этим

;

Логарифмируя, получаем:

;

или

Поскольку i_k отрицательно, в этих уравнениях под знаком логарифма стоит абсолютное ее значение.

В дальнейшем изложении мы не будем пользоваться обозначением |i_k|, но будем помнить, что i_k есть абсолютное значение катодной плотности тока. Кроме того, под знаком логарифма должна стоять плотность тока в безразмерных единицах, например в долях плотности тока обмена. Этим требованием обычно пренебрегают и выражают i_k в А/м².

Оба уравнения могут быть представлены в форме

η = a + b lg |i|

носящей название уравнения Тафеля.

Построение катодной и анодной поляризационных кривых в полулогарифмических координатах позволяет определить значение плотности тока обмена, а также коэффициенты переноса (рис. 8.8). Экстраполяция линейных участков, подчиняющихся уравнению Тафеля, на нулевое перенапряжение дает значение логарифма плотности тока обмена.

По углам наклона линейных участков в координатах η — lg i определяют коэффициенты переноса:

;

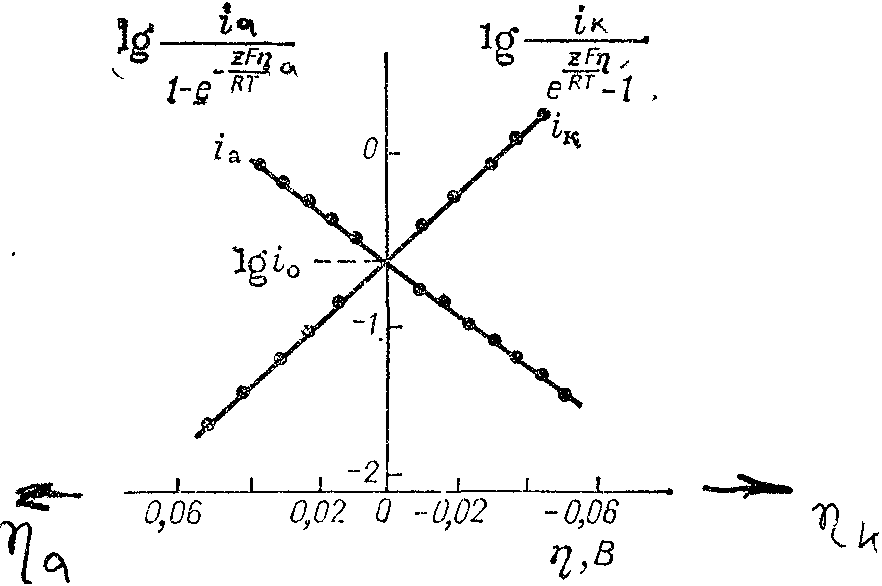
Рис. 8.8. Зависимость перенапряжения от плотности тока на амальгамном кадмиевом электроде в растворе CdSO₄ (концентрации 0,005 кмоль/м³) + K₂SO₄ (концентрации 0,4 кмоль/м³).

Рис. 8.9. Поляризационные кривые на амальгамном цинковом электроде в растворе перхлората цинка в диметилформамиде, построенные в координатах О. А. Есина.

Как показал О. А. Есин, уравнение полной поляризационной кривой может быть проанализировано и в общей форме. Вынося в этом уравнении один из членов разности за скобки и помня, что α_k + α_a = 1, получим:

или

Преобразовываем далее:

;

или

Два последних уравнения выражают соответственно истинные скорости анодного и катодного процессов и справедливы во всей области перенапряжений. Каждое из уравнений представляет прямую линию в координатах η — ( η — ) (рис. 8.9). Обе прямые проходят в области катодных и анодных перенапряжений и соответствуют истинной скорости анодного и катодного процессов как в катодной, так и в анодной областях перенапряжений. Прямые пересекаются при η = 0 и их точка пересечения на оси ординат дает значение логарифма плотности тока обмена. Коэффициенты переноса определяются из уравнений:

;

Используя выражения для частных поляризационных кривых, можно получить уравнение для равновесного потенциала. Так как i₁ = i₂ при Е = Е_p, получим:

и

Учитывая, что α_a + α_k = 1, имеем:

Сравнивая последнее выражение с уравнением Нернста, получим:

Таким образом, стандартный потенциал электродной реакции зависит от соотношения констант скоростей катодного и анодного процессов.

Уравнения для частных поляризационных кривых при постоянных значениях а_Ox и a_Red в координатах Е — lg i являются прямыми линиями. По координатам точки пересечения прямых могут быть определены логарифмы плотности тока обмена и равновесный потенциал. Такой способ определения i₀ и Е_p часто применяется, так как не на всех электродах можно непосредственно измерить равновесный потенциал. Это связано с тем, что многие из электродов (Fe, Ni в растворах собственных ионов), а также некоторые окислительно-восстановительные электроды, имеют низкие токи обмена. В равновесных условиях на основную реакцию обмена накладываются побочные процессы, которые возникают в результате присутствия примесей на металле (окислы) или в растворе. Возможно также протекание неравновесных коррозионных процессов. Результатом является смещение измеряемого потенциала от равновесного потенциала основной реакции. Кроме того, при низких токах обмена равновесие устанавливается медленно.

Экстраполируя поляризационные кривые из области высоких катодных и анодных потенциалов, в отдельных случаях удается избежать влияния побочных процессов. С одной стороны, это связано с тем, что вклад в общий ток тока восстановления примеси незначителен ввиду малости ее концентрации, а с другой стороны — при этих потенциалах побочные реакции могут не протекать.

Как показывают экспериментальные данные, равновесные потенциалы, определенные из кинетических измерений, хорошо совпадают, когда это возможно, с полученными из измерения равновесий, и их совпадение является критерием обратимости электродной реакции (или истинного равновесия на электроде).