5.1.1. Электронная проводимость

Металлы, характеризующиеся небольшой энергией перехода электрона из валентной зоны в зону проводимости, уже при нормальной температуре имеют в зоне проводимости достаточное число электронов для обеспечения высокой электрической проводимости. Проводимость металлов уменьшается с повышением температуры. Это происходит из-за того, что с ростом температуры в металлах преобладает эффект увеличения колебательной энергии ионов кристаллической решетки, оказывающий сопротивление направленному движению электронов, над эффектом увеличения числа носителей заряда в зоне проводимости. Сопротивление химически чистых металлов с повышением температуры возрастает, увеличиваясь примерно на 4∙10^–3 R₀ при повышении температуры на градус (R₀ — сопротивление при 0°С). Для большинства химически чистых металлов при нагревании наблюдается прямолинейная зависимость между сопротивлением и температурой

R = R₀ (1 + αt)

где α — температурный коэффициент сопротивления.

Температурные коэффициенты сплавов могут изменяться в широких пределах, например, у латуни α = 1,5∙10^–3, а у константана α = 4∙10^–6.

Удельная проводимость металлов и сплавов лежит в пределах 10⁶ — 7∙10⁷ См/м. Электрическая проводимость металла зависит от числа и заряда электронов, участвующих в переносе тока, и среднего времени пробега между столкновениями. Эти же параметры при данной напряженности электрического поля определяют и скорость движения электрона. Поэтому плотность тока в металле может быть выражена уравнением

где — средняя скорость упорядоченного движения зарядов; п – число электронов зоны проводимости в единице объема.

Полупроводники по своей проводимости занимают промежуточное положение между металлами и изоляторами. Чистые полупроводниковые материалы, например германий и кремний, обладают собственной проводимостью.

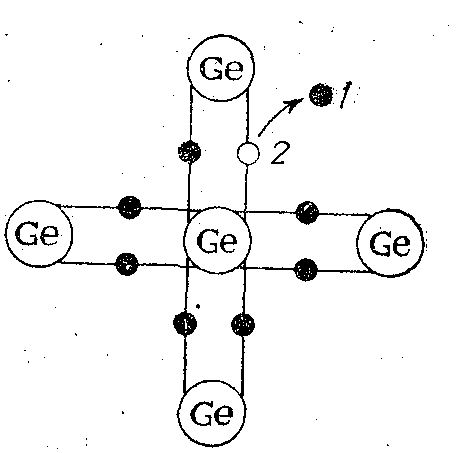
Рис. 5.1. Схема возникновения пары электрон проводимости (1) – дырка (2).

Собственная проводимость обусловлена тем, что при тепловом возбуждении электронов происходит их переход из валентной зоны в зону проводимости. Эти электроны под действием разности потенциалов движутся в определенном направлении и обеспечивают электронную проводимость полупроводников. При переходе электрона в зону проводимости в валентной зоне остается вакантное место — «дырка», эквивалентное присутствию единичного положительного заряда. Дырка также может перемещаться под действием электрического поля в результате перескока на ее место электрона валентной зоны, но в сторону, противоположную движению электронов зоны проводимости, обеспечивая дырочную проводимость полупроводника. Процесс образования дырки показан на рис. 5.1.

Таким образом, в полупроводнике с собственной проводимостью имеется два типа носителей заряда— электроны и дырки, которые обеспечивают электронную и дырочную проводимость полупроводника.

В полупроводнике с собственной проводимостью число электронов в зоне проводимости равно числу дырок в валентной зоне. При данной температуре в полупроводнике существует динамическое равновесие между электронами и дырками, т. е. скорость их образования равна скорости рекомбинации. Рекомбинация электрона зоны проводимости с дыркой валентной зоны приводит к «образованию» электрона в валентной зоне.

Удельная проводимость полупроводника зависит от концентрации носителей заряда, т. е. от их числа в единице объема. Обозна-чим концентрацию электронов n_i, а концентрацию дырок р_i. В полупроводнике с собственной проводимостью n_i = p_i (такие полупроводники кратко называются полупроводниками i-типа). Концентрация носителей заряда, например в чистом германии, равна n_i = p_i ≈10¹⁹ м^–3, в кремнии — примерно 10¹⁶ м^–3 и составляет 10^–7 — 10^–10 % по отношению к числу атомов N.

Под действием электрического поля в полупроводнике происходит направленное движение электронов и дырок. Плотность тока проводимости складывается из электронной i_e и дырочной i_p плотностей токов: i = i_e + i_p, которые, несмотря на равенство концентраций носителей, не равны по величине, так как скорости движения (подвижности) электронов и дырок различны. Плотность электронного тока равна:

Средняя скорость движения электронов пропорциональна напряженности Е' электрического поля:

91

Коэффициент пропорциональности w_e⁰ характеризует скорость движения электрона при единичной напряженности электрического поля и называется абсолютной скоростью движения. При комнатной температуре в чистом германии w_e⁰ = 0,36 м²/(В∙с).

Из двух последних уравнений получаем:

Повторив аналогичные рассуждения для дырочной проводимости, можем записать:

Тогда для полной плотности тока:

Сравнивая выражение для i с законом Ома i = κЕ', при S = 1 м² получим:

Как указано выше, у полупроводника с собственной проводимостью n_i = p_i, следовательно

w_p⁰ всегда ниже w_e⁰, например в германии w_p⁰ = 0, 18 м²/(В∙с), а w_e⁰ = 0,36 м²/(В∙с).

Таким образом, удельная электрическая проводимость полупроводника зависит от концентрации носителей и их абсолютных скоростей и аддитивно складывается из двух членов:

κ_i = κ_e + κ_p

Закон Ома для полупроводников выполняется лишь в том случае, если концентрация носителей n_i не зависит от напряженности поля. При высоких напряженностях поля, которые называются критическими (для германия E_кр’ = 9∙10⁴ В/м, для кремния E_кр’ = 2,5∙10⁴ В/м), закон Ома нарушается, что связано с изменением энергии электрона в атоме и снижением энергии перевода в зону проводимости, а также с возможностью ионизации атомов решетки. Оба эффекта вызывают увеличение концентрации носителей заряда.

Электрическая проводимость при высоких напряженностях поля выражается эмпирическим законом Пуля:

ln κ = ln κ₀ + α (E’ – E_кр’)

где κ₀ — удельная проводимость при Е’ = Е_кр’.

При повышении температуры в полупроводнике происходит интенсивная генерация носителей заряда, причем их концентрация увеличивается быстрее, чем уменьшается абсолютная скорость движения электронов из-за теплового движения. Поэтому, в отличие

от металлов, электрическая проводимость полупроводников с по- вышением температуры возрастает. В первом приближении для небольшого интервала температур зависимость удельной проводимости полупроводника от температуры может быть выражена уравнением

где k — постоянная Больцмана; А — энергия активации (энергия, необходимая для перевода электрона в зону проводимости).

Вблизи абсолютного нуля все полупроводники являются хорошими изоляторами. С повышением температуры на градус их проводимость увеличивается в среднем на 3 — 7%.

При введении в чистый полупроводник примесей к собственной электрической проводимости добавляется примесная электрическая проводимость. Если, например, в германий вводить элементы V группы периодической системы (Р, As, Sb), то последние образуют решетку с германием с участием четырех электронов, а пятый электрон, в связи с малой энергией ионизации атомов примеси (около 1,6∙10^–21), переходит от атома примеси в зону проводимости. В таком полупроводнике будет преобладать электронная проводимость (полупроводник называется электронным полупроводником п-типа]. Если атомы примеси обладают большим сродством к электрону, чем германий, например элементы III группы (In, Ga, В, А1), то они отнимают электроны от атомов германия и в валентной зоне образуются дырки. В таких полупроводниках преобладает дырочная проводимость (полупроводник р-типа]. Атомы примесей, обеспечивающие электронную проводимость, являются донорами электронов, а дырочную — акцепторами) .

Примесные полупроводники обладают более высокой электрической проводимостью, чем полупроводники с собственной проводимостью, если концентрация атомов донорной N_Д или акцепторной N_А примеси превышает концентрацию собственных носителей заряда. При больших значениях N_Д и N_A можно пренебречь концентрацией собственных носителей. Носители заряда, концентрация которых преобладает в полупроводнике, называются основными. Например, в германии n-типа n_n ≈ 10²² м^–3, в то время как n_i ≈ 10¹⁹ м~³, т. е. концентрация основных носителей в 10³ раз превышает концентрацию собственных носителей.

Для примесных полупроводников справедливы соотношения:

n_np_n = n_ip_i = n_i² = p_i²

n_pp_p = n_ip_i = n_i² = p_i²

Первое из этих уравнений записано для полупроводника n-типа, а второе — для полупроводника р-типа. Из данных соотношений следует, что очень небольшое количество примеси (около 10^{–4 0}/о) значительно увеличивает концентрацию носителей заряда, в результате чего электрическая проводимость возрастает.

Если пренебречь концентрацией собственных носителей и считать N_Д ≈n_n для полупроводника n-типа и N_A ≈ р_р для полупроводника р-типа, то удельная электрическая проводимость примесного полупроводника может быть выражена уравнениями:

При наложении электрического поля в полупроводниках n-типа перенос заряда осуществляется электронами, а в полупроводниках р-типа — дырками.

При внешних воздействиях, например при облучении, концентрация носителей заряда изменяется и может быть разной в различных частях полупроводника. В этом случае, как и в растворах, в полупроводнике протекают процессы диффузии. Закономерности Процессов диффузии подчиняются уравнениям Фика. Коэффициенты диффузии носителей заряда значительно выше, чем ионов в растворе. Например, у германия коэффициент диффузии электронов равен 98∙10^–4 м²/с, дырок — 47∙10^–4 м²/с. Типичными полупроводниками, помимо германия и кремния, при комнатной температуре являются ряд оксидов, сульфидов, селенидов, телуридов и т. д. (например, CdSe, GaP, ZnO, CdS, SnO₂, In₂O₃, InSb).