4.3. Константы образования комплексных ионов

При образовании комплексных ионов присоединение лиганда L* к центральному иону М^z+ происходит ступенчато:

M^z+ + L = M^z+L

M^z+L + L = M^z+L₂

……………………

M^z+L_i–1 + L = M^z+L_i

……………………

M^z+L_n–1 + L = M^z+L_n

Концентрационные константы равновесия для этих реакций могут быть записаны следующим образом:

……………………….

……………………….

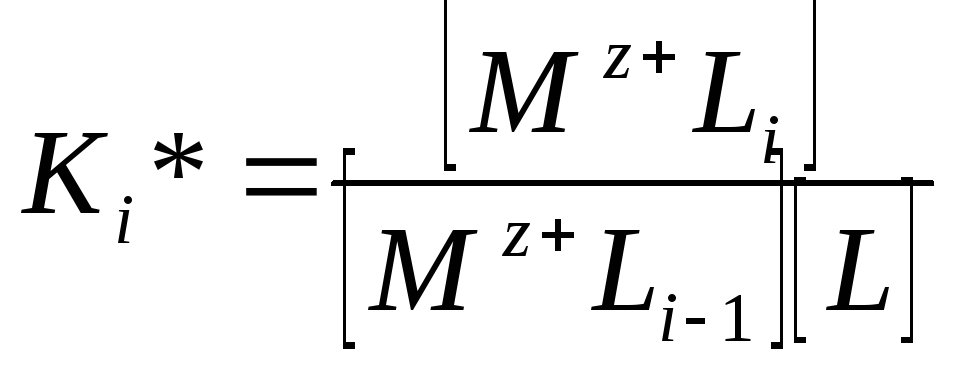
Константы K₁* — К_n* называются концентрационными ступенчатыми константами образования комплексных ионов. Однако для расчетов удобнее использовать общие константы образования.

* Лиганд может быть как нейтральной частицей, так и ионом. Для упрощения записи заряд лиганда опущен.

В этом случае реакции образования комплексных ионов записываются следующим образом

M^z+ + L = M^z+L

M^z+ + 2L = M^z+L₂

……………………

M^z+ + iL = M^z+L_i

……………………

M^z+ + nL = M^z+L_n

и выражения для концентрационных общих констант образования

будут

……………………….

……………………….

Из сравнения выражений для общих и ступенчатых констант образования (устойчивости) видно, что:

β₁ = K₁

β₂ = K₁K₂

………………..

β_i = K₁K₂ … K_i

……………………….

Β_n = K₁K₂ … K_i … K_n

Величины, обратные общим константам устойчивости, называются константами нестойкости:

Уравнения материального баланса по катионам и анионам для растворов, содержащих комплексные ионы с аналитическими концентрациями катиона C₁ и аниона C₂, будут иметь вид:

C₁ = [M^z+] + [M^z+L] + … + [M^z+L_i] + … + [M^z+L_n]

C₂ = [L^–] +[M^z+L] + … + 2[M^z+L₂] + … + i[M^z+L_i] + … + n[M^z+L_n]

Выражая равновесные концентрации комплексов через общие константы устойчивости, получим:

C₁ = [M^z+] (1 + β₁ [L] + β₂ [L]² + … + β_i [L]ⁱ + … + β_n [L]ⁿ)

или

Рис, 4.1. Распределительная диаграмма для иодидных комплексов цинка в растворе диметилформамида.

Зависимость долей сольватированных ионов цинка (1), ZnI⁺ (2), ZnI₂ (3), ZnI₃^– (4) и ZnI₄^2– (5) от концентрации иодида лития.

При исследовании электрохимического восстановления или окисления комплексных ионов, когда в растворе существует несколько сортов частиц, важное значение имеет знание равновесных концентраций каждой из них. Наиболее наглядное представление о составе раствора дают кривые распределения (или распределительные диаграммы), которые показывают зависимость доли аи каждого сорта комплексов от концентрации лиганда C_L (рис 4.1). Долей комплекса называется отношение его равновесной концентрации при данной концентрации лиганда к аналитической концентрации катионов. В соответствии с этим определением доля простых незакомплексованных ионов в растворе равна:

α₀ = [M^z+]/C₁

Подставляя выражение для С₁, получим:

Доли других частиц будут:

……………………………………….

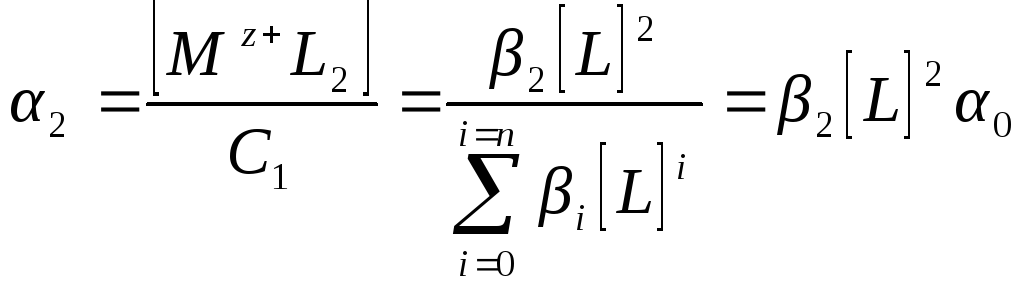
Так как концентрация всех ионов металла в растворе равна то

α₀ + α₁ + α₂ + … +α_i + … +α_n = 1

при любой концентрации лиганда.

Равновесные концентрации каждого вида комплексов в растворе могут быть рассчитаны, если известны константы устойчивости и равновесные концентрации ионов металла и лиганда.

4.4. Ступенчатая диссоциация электролитов

Диссоциация многоосновной кислоты, имеющей, например, п атомов водорода, способных ионизироваться, протекает в п последовательных стадий:

H_nA + H₂O = H₃O⁺ + H_n–1A^–

H₂O + H_n–1A^– = H₃O⁺ + H_n–2A^2–

H₂O + H_n–2A^2– = H₃O⁺ + H_n–3A^3–

……………………………………

H₂O + HA^n–1 = H₃O⁺ + A^n–

Концентрационная константа диссоциации для каждого из выше написанных уравнений равновесия будет иметь свое значение и определяться соответствующим выражением:

………………………………

Концентрация Н₂О постоянна и включена в К*.

Константы диссоциации зависят от структуры молекул кислот, причем константа диссоциации каждого последующего атома водорода меньше константы диссоциации предыдущего, т. е. K₁* > > K₂* > K₃* > … > K_n* Значение каждой последующей константы составляет ~ 1/100000 от предыдущей. Эта закономерность является общей для тех кислородсодержащих кислот, у которых все ОН^–-группы связаны с одним и тем же атомом. Например, диссоциация фосфорной кислоты протекает по схеме:

H₂O + H₃PO₄ = H₃O⁺ + H₂PO₄^–

H₂O + H₂PO₄^– = H₃O⁺ + HPO₄^2–

H₂O + HPO₄^2– = H₃O⁺ + PO₄^3–

Константы диссоциации определяются следующими выражениями

и имеют соответственно значения 5,9∙10^–3; 6,2∙10^–8; 4,8∙10^–13.

Равновесные концентрации разных сортов частиц рассчитываютметодом, аналогичным изложенному при рассмотрении комплекс-ных ионов (см. 4.3).

Материальный баланс для фосфат-иона при диссоциации фосфорной кислоты, аналитическая концентрация которой равна С, запишется так:

[H₃PO₄] + [H₂PO₄^–] + [HPO₄^2–] + [PO₄^3–] = C

Определим равновесные концентрации частиц из констант диссоциации и, подставляя их в уравнение материального баланса, получим:

Доля кислоты, присутствующей в виде определенной формы, является отношением равновесной концентрации этой формы к аналитической концентрации, например

Следовательно

Доли других частиц будут определяться выражениями:

Уравнение материального баланса может быть записано также следующим образом:

α₁ + α₂ + α₃ α₀ = 1

Рис. 4,2. Распределительная диаграмма фосфорной кислоты.

Равновесные концентрации каждого сорта частиц, присутствующих при диссоциации многоосновной кислоты, рассчитываются, если известны константы

диссоциации и равновесные концентрации, кислоты и ионов водорода.

На рис. 4.2 приведена зависимость α — рН, полученная при использовании констант ионизации, приведенных выше.

Интересен тот факт, что в растворе фосфорной кислоты присутствует либо только один сорт частиц фосфорной кислоты, либо два сорта каких-либо частиц в сравнимых концентрациях, в зависимости от интервала изменения рН, но ни в одном интервале рН не находится сразу три сорта частиц.