Властивості визначників

1. Визначник не змінюється при транспонуванні матриці. Отже, при обчисленні визначника його рядки та стовпчики є рівноправними.

2. Якщо визначник містить нульовий рядок (стовпчик), то він дорівнює нулю.

3. Якщо всі елементи рядка (стовпчика) визначника мають спільний множник, то цей множник можна винести за знак визначника.

4. При перестановці двох довільних рядків (стовпчиків) визначника, визначник змінює знак на протилежний.

5. Якщо визначник містить два однакових рядки (стовпчики), то він дорівнює нулю.

6. Якщо визначник містить два пропорційних рядки (стовпчики), то він дорівнює нулю.

7. Сума добутків елементів одного рядка (стовпчика) визначника на алгебраїчні доповнення до елементів іншого рядка (стовпчика) цього визначника, дорівнює нулю.

8. Визначник добутку матриць дорівнює добутку визначників цих матриць: 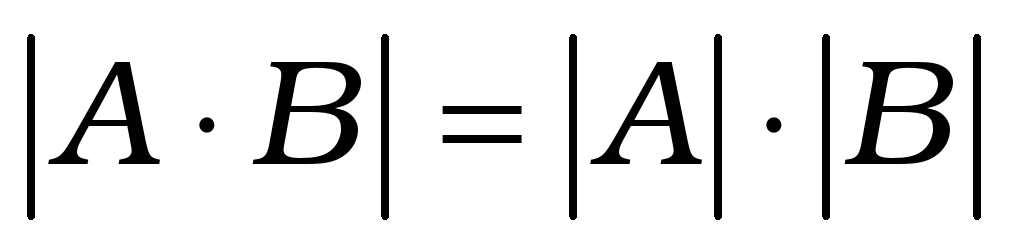. З цієї властивості слідує, що хоча , але .

9. Визначник не зміниться, якщо до елементів довільного його рядка (стовпчика) додати відповідні елементи іншого його рядка (стовпчика), помножені на довільне число.

Зауваження. Остання властивість використовується для спрощення елементів визначника перед використанням теореми Лапласа.

Приклад 6. Обчислити визначник: .

Користуючись властивістю 3, винесемо спільний множник з першого стовпчика: =. Користуючись властивістю 9, перетворимо визначник так, щоб всі елементи третього стовпчика обертались в нуль, крім одного елементу. Цей елемент називається ведучим. Нехай ведучим елементом, наприклад, буде одиниця, розташована у третьому рядку та третьому стовпчику. Додамо до елементів першого рядка відповідні елементи третього рядка, помножені на 3; до елементів другого рядка додамо відповідні елементи третього рядка. Після цього розкладемо отриманий визначник за третім стовпчиком, користуючись теоремою Лапласа.

==.

Останній визначник можна порахувати за правилом трикутників або продовжити його спрощення. Винесемо спільний множник елементів другого стовпчика за знак визначника та зробимо нульовими елементи цього стовпчика, вибираючи за ведучий його елемент з третього рядка. Після чого розкладемо отриманий визначник за цим стовпчиком.

==

===48.

§ 3. Обернена матриця

Нагадаємо, що оберненою до матриці А називається матриця , яка задовольняє співвідношення , де Е – одинична матриця, обернена матриця може існувати лише для квадратних матриць, але не кожна квадратна матриця має обернену.

Якщо визначник матриці А не дорівнює нулю, ця матриця називається невиродженою, інакше матриця А називається виродженою.

Теорема (необхідна та достатня умова існування оберненої матриці). Обернена до матриці А матриця існує, причому єдина тоді й тільки тоді, коли матриця А є невиродженою. При цьому

=,

де матриця складається з алгебраїчних доповнень до кожного елементу матриці і називається приєднаною.

Проілюструємо на прикладах використання останньої формули для знаходження оберненої матриці.

Приклад 7. Обчислити обернену для довільної матриці другого порядку: .

Обернена матриця буде існувати, якщо , тобто .

Знайдемо алгебраїчні доповнення до елементів матриці А:

, ,

, .

Отже, приєднана матриця . Порівнюючи з початковою матрицею, легко помітити, що для побудови приєднаної для матриці другого порядку потрібно елементи головної діагоналі поміняти місцями, а у елементів побічної діагоналі поміняти знак.

Таким чином, обернена матриця .

Приклад 8. Обчислити обернену до матриці .

Визначник матриці , отже існує єдина обернена матриця.

Алгебраїчні доповнення до елементів матриці А дорівнюють:

, , ,

, , ,

, , .

Отже, обернена матриця .

Очевидно, кількість обчислень сильно зростає з ростом порядку матриці, зокрема для обчислення оберненої до матриці четвертого порядку необхідно підрахувати 16 алгебраїчних доповнень, які складаються з визначників третього порядку. Тому для знаходження обернених до матриць вищих порядків використовується інший метод – метод елементарних перетворень.

Алгоритм методу елементарних перетворень полягає в наступному: справа від матриці А дописують одиничну матрицю такого ж порядку, шляхом елементарних перетворень над рядками матриці А її намагаються звести до одиничної, ті ж перетворення в тому самому порядку здійснюються над відповідними рядками одиничної матриці. Як тільки матриця А перетвориться на одиничну, на місці одиничної матриці буде знаходитись обернена матриця .

При використанні методу елементарних перетворень не потрібно обчислювати визначник матриці А, тому з’ясувати, чи існує обернена до неї можна лише під час реалізації методу, а саме: якщо на певному кроці перетворень у матриці А виникне нульовий рядок, то вона є виродженою і оберненої не має. Інакше обернена існує, причому єдина.