
- •Издание училища
- •В.1. Место рлс в радиолокационной системе
- •Глава 1. Основные характеристики рлс и требования, предъявляемые к ним
- •1.1. Общие сведения
- •1.2. Состав радиолокационной информации
- •1.3. Зона обзора
- •1.4. Точность измерения координат
- •1.5. Разрешающие способности по координатам
- •1.6. Помехозащищенность
- •1.7. Информационная способность
- •1.8. Надежность
- •1.9. Электромагнитная совместимость
- •1.10. Маневренные характеристики
- •Глава 2. Дальность действия рлс в различных условиях ее работы
- •2.1. Уравнение радиолокации в режиме обзора при произвольных форме зоны обнаружения и способе обзора
- •2.1.1. Вывод уравнения радиолокации
- •2.1.2. Изодальностная зона обнаружения
- •2.1.3. Изовысотная зона обнаружения
- •2.1.4. Смешанная зона обнаружения
- •2.2. Дальность действия рлс с учетом затухания радиоволн в атмосфере
- •2.3. Дальность действия рлс в условиях активных маскирующих помех
- •2.3.1. Дальность действия рлс в условиях активных шумовых маскирующих помех
- •2.3.2. Дальность действия рлс в условиях импульсных помех
- •2.4. Дальность действия рлс в условиях маскирующих пассивных помех
- •Действия рлс при включении аппаратуры защиты в условиях отсутствия пп
- •2.5. Дальность обнаружения маловысотных целей
- •2.6. Упрощенные формы записи уравнения радиолокации
- •Глава 3. Основные характеристики радиолокационных целей
- •3.1. Общие сведения
- •3.2. Статистические модели целей
- •3.3. Оценка влияния и на вероятность обнаружения цели
- •3.3.1. Оценка влияния вида плотности распределения вероятности эпц
- •3.3.2. Оценка влияния вида энергетического спектра флюктуации отраженного сигнала
- •3.4. Оценка среднего значения эффективной поверхности радиолокационных целей
- •3.4.1. Точечные (сосредоточенные) цели
- •3.4.2. Распределенные цели
- •3.5. Энергетический спектр флюктуаций сигнала, отраженного от точечной цели
- •3.6. Энергетический спектр флюктуаций сигнала, отраженного от распределенной цели
- •Глава 4. Показатели качества и параметры обнаружения
- •4.1. Общие сведения
- •4.2. Показатели качества радиолокационного обнаружения в точке
- •4.3. Показатели качества радиолокационного обнаружения за обзор
- •4.4. Период ложной тревоги
- •4.5. Интегральные вероятности правильного обнаружения и ложной тревоги
- •4.6. Выбор значений показателей качества обнаружения
- •4.7. Параметры обнаружения и связь между ними
- •4.8. Определение требуемого значения отношения сигнал—шум на входе устройства сравнения с порогом
- •5.1. Основные отличия целей и маскирующих пассивных помех
- •5.2. Пути повышения помехозащищен-ности рлс в условиях маскирующих пассивных помех
- •5.3. Выбор структуры зондирующего сигнала при работе рлс в условиях пассивных помех
- •5.4. Способы обеспечения заданного значения 1-й слепой скорости
- •5.5. Классификация систем сдц
- •5.6. Обобщенная структурная схема и основные характеристики системы сдц
- •5.7. Система сдц с эквивалентной
- •5.7.1. Структурная схема системы сдц
- •5.7.2. Основные характеристики системы
- •5.7.3. Принципы построения элементов и устройств системы сдц
- •5.7.4. Влияние нестабильностей аппаратуры на эффективность сдц
- •5.8. Системы сдц с внутренней когерентностью на базе устройств чпк на радиочастоте
- •5.9. Системы сдц с внешней когерентностью
- •5.9.1. Система сдц с некогерентной компенсацией пп
- •5.9.2. Система сдц с помеховым гетеродином
- •5.9.3. Основные характеристики систем
- •5.10. Системы сдц на базе автокомпенсаторов
- •5.10.1. Структурная схема
- •5.10.2. Основные характеристики чпак
- •5.10.3. Требования к функциональным элементам чпак и их обеспечение
- •5.11. Фильтровые и корреляционно-фильтровые системы сдц
- •5.11.1. Фильтровые системы сдц
- •5.11.2. Корреляционно-фильтровые системы сдц
- •5.11.3. Основные характеристики систем
- •6.2.2. Шумовая автоматическая регулировка усиления
- •6.2.3. Усилители с логарифмической амплитудной характеристикой
- •6.2.4. Автоматическая регулировка порога ограничения
- •6.3. Повышение помехозащищенности за счёт увеличения плотности потока энергии зондирующего сигнала
- •6.4. Технические решения, обеспечивающие защиту рлс методом пространственной селекции
- •6.4.1. Основные пути реализации метода пространственной селекции
- •6.4.2. Уменьшение угловых размеров главного лепестка диаграммы направленности
- •6.4.3. Снижение уровня боковых лепестков
- •6.4.4. Уменьшение уровня приёма в направлениях на постановщики активных помех
- •6.5. Технические решения, обеспечивающие защиту рлс от помех по главному лепестку диаграммы направленности
- •6.6. Принципы построения систем перестройки рабочей частоты рлс
- •6.6.1. Требования к параметрам системы перестройки станции
- •6.6.2. Структурная схема спс
- •6.7. Устройства защиты рлс от импульсных помех
- •6.7.1. Виды импульсных помех
- •6.7.2. Устройства защиты от узкополосных импульсных помех
- •6.7.3. Устройства защиты от широкополосных импульсных помех
- •6.7.4. Устройства защиты от несинхронных импульсных помех
- •6.7.5. Особенности построения устройств защиты от оип
- •6.8. Принципы построения анализаторов помеховои обстановки в адаптивных рлс
- •Глава 7. Принципы построения аппаратуры пеленгации постановщиков активных помех
- •7.1 Требования предъявляемые к аппаратуре пеленгации
- •7.2. Обобщенная структурная схема и варианты технической реализации аппаратуры пеленгации
- •8.Обеспечение электромагнитной совместимости рлс
- •8.1. Пути обеспечения электромагнитной совместимости рлс
- •8.2. Технические решения, обеспечивающие ослабление неосновных излучений рлс
- •8.3. Технические решения, обеспечивающие ослабление приема по неосновным каналам
- •Глава 9. Потери в тракте приёма и выделения сигналов из помех и технические решения, обеспечивающие их снижение
- •9.1 Обобщенная структурная схема тракта приёма и выделения сигналов из помех
- •9.2. Потери в приёмной антенне
- •9.3. Потери в тракте высокой частоты на прием
- •9.3.1. Обобщенная структурная схема тракта высокой частоты импульсной рлс
- •9.3.2. Методика учета потерь в тракте высокой частоты
- •9.4. Потери за счет рассогласования частотной характеристики линейной части приемника и частотного спектра сигнала
- •9.4.1. Составляющие коэффициента потерь Lрф
- •9.4.2. Потери рассогласования, обусловленные наличием побочных каналов приема
- •Потери рассогласования,обусловленные неоптимальностью формы ачх линейной части приёмника
- •9.4.3. Потери рассогласования, обусловленные расстройкой приёмника по частоте
- •9.5. Требования к системам апч и технические решения, обеспечивающие их выполнение
- •9.6. Потери интегрирования
- •9.7. Принципы построения рециркуляторов
- •9.7.1. Общие сведении о рециркуляторах
- •9.7.2. Рециркулятор на базе ультразвуковой линии задержки
- •9.7.3. Требования к функциональным элементам рециркулятора
- •9.7.4. Многоступенчатые рециркуляторы
- •9.8. Накопители на электронно-лучевой трубке
- •9.9. Комплексирование накопителей
- •9.10. Потери. Обусловленные накоплением дополнительного шума
- •9.10.1. Причины возникновения потерь
- •9.10.2. Объединение сигналов в рлс с парциальной диаграммой направленности на приём
- •9.10.3. Накопление дополнительного шума на экране элт
- •9.10.4. Накопление дополнительного шума в вус
- •9.11. Потери за счет ограничения сигналов сверху
- •9.12. Потери за счет нестабильности порогового уровня и коэффициента усиления приёмника
- •9.13. Потери за счет нестационарности помех на входе системы обработки сигналов
- •9.13.1. Причины нестационарности помех
- •9.13.2. Стабилизация вероятности ложной тревоги в условиях отражений от протяженных источников пп
- •9.13.3. Непараметрические обнаружители
- •9.14. Потери, связанные с работой оператора
- •9.15. Методика учета потерь в тракте приёма и выделения сигналов
- •Глава 10. Обеспечение требований к параметрам зондирующего сигнала
- •10.1. Параметры зондирующего сигнала и их влияние на характеристики рлс
- •10.2. Основные типы передающих устройств и их сравнительная характеристика
- •Глава 11. Влияние способа обзора зоны обнаружения на характеристики рлс
- •11.1. Виды и способы обзора зоны
- •11.2. Сравнение способов обзора зоны обнаружения при отсутствии потерь
- •11.3. Сравнение способов обзора зоны обнаружения при наличии потерь
- •11.4. Возможности уменьшения числа парциальных каналов в трехкоординатных рлс
- •Глава 12. Обеспечение требований к точности измерения координат
- •12.1. Общие сведения об ошибках измерения. Связь между ошибками
- •12.2. Ошибки измерения дальности и технические решения, обеспечивающие их снижение
- •12.2.1. Потенциальная ошибка измерения дальности
- •12.2.2. Ошибка измерения дальности за счет особенностей распространения радиоволн
- •12.2.3. Инструментальная ошибка измерения дальности
- •12.2.4. Динамическая ошибка
- •12.3. Ошибки измерения угловых координат и технические решения, обеспечивающие их снижение
- •12.3.1. Потенциальная ошибка
- •12.3.2. Ошибки измерения угловых координат за счёт особенностей распространения радиоволн
- •12.3.3. Инструментальная ошибка измерения угловых координат
- •12.4.1. Уравнение высоты
- •К разрешающим способностям рлс по координатам
- •13.5. Реальная разрешающая способность рлс по высоте
- •13.6. Вероятность разрешения целей в группе
- •Глава 14 особенности построения рлс с широкополосными зондирующими сигналами
- •Глава is. Особенности построения рлс с электронным управлением лучом
- •Глава 16. Особенности построения мс с цифровой обработкой сигналов
- •16,3.1. Общие понятия
- •16.3.3. Устройство квантования
- •16.3.4, Параметры ацп
- •16.3.5. Типы ацп
- •16.4.1. Обнаружитель типа движущегося окна
- •16.5. Особенности построения цифровых обнаружителей
- •16.5.1. Вычислитель модуля
- •16.5.2. Цифровые накопители
- •16.7.2. Особенности технической реализации цгфп,
- •16.7,3. Особенности технической реализаций
- •16.8. Цифровые авто компенсаторы
- •Глава 1. Основные характеристики рлс и требования, предъявляемые
- •Глава 2. Дальность действия рлс в различных условиях ее работы . 22
- •Глава 3. Основные характеристики радиолокационных целей ... 43
- •Глава 4. Показатели качества и параметры обнаружения .... 59
- •Глава 5 Обеспечение требуемой помехозащищенности рлс и условиях
- •Глава 7. Принципы построения аппаратуры пеленгации постщювщиков
- •Глава 8. Обеспечение электромагнитной совместимости рлс . . . F79
- •Глава 10. Обеспеченно требований к параметрам зондирующего сигнала 22s1
- •Глава 13. Обеспечение требований к разрешающим способностям рлс
- •[6.Я. Цифровые Ёвтокомпевсаторы 345
2.1.2. Изодальностная зона обнаружения
Будем
полагать, что в процессе
обзора зоны антенный луч приемной
антенны не изменяет своей ширины
![]() =
1 при
=
1 при
![]() .
Примером РЛС, в которой выполняется
это условие, является радиолокационный
высотомер с механическим качанием
антенны в вертикальной плоскости.
.
Примером РЛС, в которой выполняется
это условие, является радиолокационный
высотомер с механическим качанием
антенны в вертикальной плоскости.
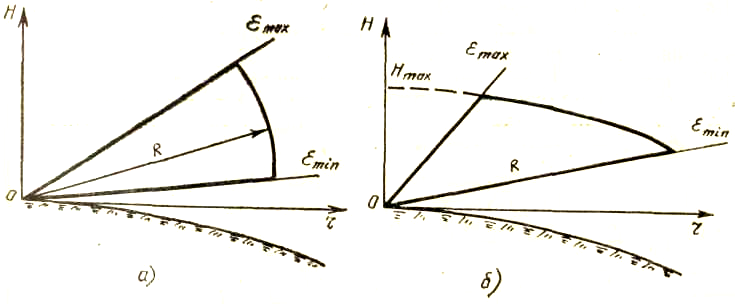
Рис. 2. 2. Зона обнаружения: а — изодальностная; б — изовысотная
В
случае изодальностной
зоны (рис. 2.2а)![]() ,
( здесь
,
( здесь
![]() —
угловой размер зоны обзора в азимутальной
плоскости). Поэтому интеграл в знаменателе
уравнения (2.12)
—
угловой размер зоны обзора в азимутальной
плоскости). Поэтому интеграл в знаменателе
уравнения (2.12)
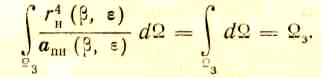
Выразим
телесный угол изодальностной зоны
обнаружения
![]() через
угловые размеры зоны в азимутальной и
угломестной плоскостях.
Учтем для этого соотношение (2.10)
через
угловые размеры зоны в азимутальной и
угломестной плоскостях.
Учтем для этого соотношение (2.10)
![]()
Подставляя
значение![]() в
исходное уравнение (2.12), получаем
в
исходное уравнение (2.12), получаем
![]()
2.1.3. Изовысотная зона обнаружения
Дальность до точек граничной поверхности в случае изовысотной зоны обнаружения (рис. 2.2б) определяется выражением
![]() (2.15)
(2.15)
Рассмотрим два способа формирования зоны.
1)
В процессе обзора зоны антенный луч
приемной антенны не изменяет
своей ширины, т. е.
![]() =
1 в пределах угловых размеров
зоны. Требуемая форма зоны обнаружения
в этом случае
может формироваться за счет изменения
в угломестной плоскости
величины излучаемой средней мощности
или коэффициента усиления
передающей антенны по закону
=
1 в пределах угловых размеров
зоны. Требуемая форма зоны обнаружения
в этом случае
может формироваться за счет изменения
в угломестной плоскости
величины излучаемой средней мощности
или коэффициента усиления
передающей антенны по закону
![]()
С учетом выражения (2.15)
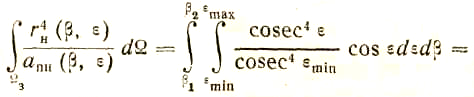
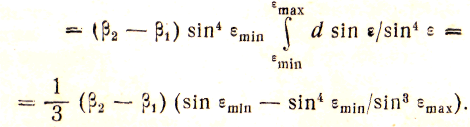
При записи формулы (2.16) учтено, что
![]() (2.16)
(2.16)
Подставляя (2.16) в исходное уравнение (2.12), получаем
![]() (2.17)
(2.17)
2) В процессе обзора зоны эффективная площадь приемной антенны изменяется в угломестной плоскости по косеканс-квадратному закону
![]() (2.18)
(2.18)
По такому же закону изменяется и коэффициент усиления передающей антенны.
Подобное изменение эффективной площади приемной антенны и коэффициента усиления может быть обеспечено, например, за счет соответствующего выбора конфигурации зеркала антенны в вертикальной плоскости или за счет использования нескольких облучателей (приемлемое приближение к косеканс-квадратной диаграмме направленности можно получить с помощью всего лишь двух облучателей [5]).
Интеграл в уравнении (2.12) для рассматриваемого случая с учетом соотношений (2.15) и (2.18)
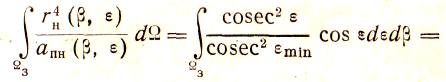
![]() (2.19)
(2.19)
и уравнение можно представить в виде
![]() ' (2.20)
' (2.20)
Сравним между собой рассмотренные варианты формирования изовысотной зоны по величине энергии, излучаемой в зону за время однократного обзора. При этом будем полагать, что все прочие параметры РЛС в обоих случаях одинаковы.
Из сопоставления уравнений (2.17) и (2.20) следует
![]()
где
![]() —
энергия, излучаемая в зону при вариантах
обзора
2
и 1
соответственно.
—
энергия, излучаемая в зону при вариантах
обзора
2
и 1
соответственно.
При
![]() (на
практике это условие, как правило,
выполняется)
записанное выше соотношение можно
упростить:
(на
практике это условие, как правило,
выполняется)
записанное выше соотношение можно
упростить:
![]()
Полученный результат свидетельствует, что с энергетической очки зрения вариант 1 формирования изовысотной зоны предпочтителен (выигрыш в энергии составляет около 300 %). Кроме того, следует учитывать и тот факт, что при формировании косеканс-квадратной диаграммы направленности поверхность антенны используется неэффективно [5].
Каково же соотношение величины энергии, излучаемой в изодальностную зону и изовысотную, формируемую путем изменения излучаемой мощности в процессе обзора? Это представляет практический интерес, так как в большинстве случаев в радиолокационных высотомерах формируется изодальностная зона обнаружения, в то время как из-за ограниченной высоты полета современных средств воздушного нападения целесообразно формировать изовысотную зону обзора. Из сопоставления уравнений (2.14) и (2.17) следует
![]()
где
![]() —
энергия, излучаемая РЛС в изодальностную
зону.
—
энергия, излучаемая РЛС в изодальностную
зону.
При
![]() :
:
![]()
Таким образом, в радиолокационных высотомерах, у которых излучаемая энергия распределяется в зоне обзора равномерно, энергия расходуется весьма нерационально.
Примечание.
По аналогии со случаем изодальностной
зоны интеграл в знаменателе уравнения
(2.12) можно трактовать как телесный угол
некоторой эквивалентной изодальностной
зоны обнаружения.
Поэтому в дальнейшем для сокращения
записи уравнения радиолокации
в режиме обзора в
некоторых случаях этот интеграл будем
обозначать
![]() :
:
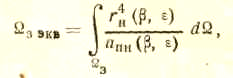
и уравнение радиолокации в режиме обзора представлять в виде
![]() (2.21)
(2.21)
