1.Составление первого опорного плана

Система ограничений задачи, решаемой симплексным методом задана в виде неравенств смысла “ ” , правые части которых в_i0. Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных переменных х₄; х₅; х₆; которые образуют базис и называются базисными переменными и определяют объемы неиспользованных ресурсов:

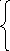х₁+х₂+х₃ + х₅ = 9800

20х₁+18х₂+30х₃+ 300х₄+ х₆ = 1200000

-8.8х₁-9.9х₂-32х₃+ 75х₄+х₇ = 15200

-32х₃+ 25х₄+х₈ = 11200

х₃+х₉ = 2000

Решим систему уравнений относительно базисных переменных:

х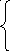₅ = 9800– (х₁+х₂+х₃)

х₆ = 1200000 – (20х₁+18х₂+30х₃+300х₄)

х₇ = 8000 – (-8.8х₁-9.9х₂-32х₃+ 75х₄)

х₈ = 11200-(-32х₃+ 25х₄)

х₉ = 2000-(х₃)

Функцию цели запишем в виде уравнения F(х) = 0 – (-150х₁ – 650х₄). Пологая что основные переменные х₁=0 х₂=0 х₃=0 х₄=0, получим первый опорный план, х₅=в₁; х₆=в₂; х₇=в₃ ;х₈=в₄ ;х₉=в₅ F(x) =0; который заносим в симплексную таблицу № 1. Она состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной и заполняется коэффициентами функции цели, взятыми с противоположным знаком.

Таблица -2. Первый опорный план

План	Базисные переменные	Свободные члены	Основные переменные				Дополнительные переменные					1
			х1	х2	х3	х4	х5	х6	Х7	Х8	Х9
I	х5	9800	1	1	1	0	1	0	0	0	0	-
	х6	1200000	20	18	30	300	0	1	0	0	0	4000
	Х7	15200	-8.8	-9.9	-32	75	0	0	1	0	0	202,667
	Х8	11200	0	0	-32	25	0	0	0	1	0	448
	Х9	2000	0	0	1	0	0	0	0	0	1	-
Индексная строка	F(x1)	0	-150	0	0	-650	0	0	0	0	0	-

2. Проверка плана на оптимальность

Если все коэффициенты индексной строки симплексной таблицы при решении задачи на максимум неотрицательны (0), то план является оптимальным.

Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план неоптимальный и его можно улучшить.

Первый опорный план, представленный в первой симплексной таблице неоптимальный, т.к. в индексной строке находятся отрицательные коэффициенты: -150; -650.

Полагая что основные переменные х₁=0; х₂=0; х₃=0, х₄=0, а дополнительные переменные х₅=9800; х₆=1200000; х₇=15200; х₈=11200; х₈=2000; F(x)=0. Следовательно, продукция не производится, а ресурсы не используются, результат равен нулю. В этом случае переходим к следующему этапу алгоритма.