§3. Вещественные линейные и квадратичные формы

Рассмотрим векторное пространство Rⁿ над полем R, в котором задан базис и пусть – произвольный вектор этого пространства, _iR.

Определение 1. Вещественной линейной формой  называется линейное отображение пространства Rⁿ в R, которое каждому ставит в соответствие число из R, где _i и _i – числа из R. Линейную форму называют также однородной формой первой степени, и чаще всего ее записывают в следующем виде:

, где .

Определение 2. Вещественной квадратичной формой  называется линейное отображение Rⁿ в R, которое каждому ставит в соответствие число из R, где – координаты вектора , – числа из R, для которых выполняется равенство .

Из определения следует, что . Поэтому квадратичная форма есть однородная форма второй степени.

Пример.

=

3.1. Приведение квадратичной формы к каноническому виду

Квадратичную форму можно записать и при помощи матрицы. Для этого вектору из Rⁿ поставим в соответствие две матрицы: матрицу-столбец 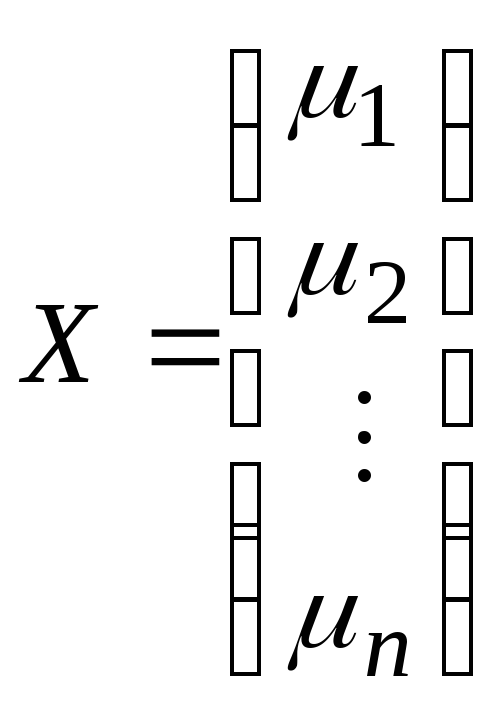и матрицу-строку X ^Т = (_ _    _n). Ясно, что X ^Т является транспонированной матрицей к X. Для коэффициентов _ij квадратичной формы введем действительную матрицу

. Тогда

.

Матрица А называется матрицей квадратичной формы и поскольку для коэффициентов квадратичной формы _ij  _ji, то матрица А является симметрической.

Рассмотрим, как изменяется матрица А при переходе в Rⁿ от одного ортонормированного базиса к другому. Обозначим матрицу перехода через Т, а координаты вектора в новом базисе через . Тогда , или в матричной форме X = TY, где Т ортогональная матрица. Поэтому для квадратичной формы имеем

, где В = Т^ТАТ.

Но так как Т ортогональна, то Т^Т = Т^–1 ; значит В = Т^–1АТ, т.е. В преобразована из А посредством матрицы Т. Кроме того, преобразованная матрица В – тоже симметрическая, ибо

В^Т = (Т^–1АТ)^Т = (Т^ТАТ)^Т = Т^ТА^Т(Т^Т)^Т = Т^ТАТ = В.

Поскольку А^Т = А.

Так как матрица А симметрическая, то Rⁿ обладает хотя бы одним ортонормированным базисом , составленным из собственных векторов матрицы А; тогда если в качестве нового базиса выбрать базис , то преобразованная матрица в этом базисе и имеет диагональный вид

здесь собственные значения _i матрицы А могут быть как различные, так и совпадающие, но все действительные. Если матрица квадратичной формы диагональная, то квадратичная форма принимает вид:

, где z₁, z₂, ... z_n – координаты вектора , разложенным по базису .

Таким образом, относительно базиса , составленного из собственных векторов матрицы квадратичной формы, квадратичная форма имеет только члены с квадратами; говорят, что она приведена к каноническому виду.

Пример. Привести к каноническому виду квадратичную форму

= 3х + 4х₁х₂ + х, где .

1. Составляем матрицу квадратичной формы:

(см. пример в начале параграфа).

2. Записываем характеристическое уравнение

, откуда    ^      .

Решая последнее уравнение, находим собственные числа: _   _  

₃  . Обозначим координаты вектора в системе собственных векторов матрицы через z₁, z₂, z₃. Тогда квадратичная форма имеет вид

.

3. Находим ортонормированные собственные вектора матрицы:

; ; . Для этого уравнение А() = записываем в координатной форме:

или

Положим . Тогда система принимает вид:

Эта сиcтема имеет единственное решение , . Величина компоненты любая. Чтобы вектор был нормированным, т.е. чтобы , примем . Имеем .

Поскольку , то система принимает вид:

Отсюда , , , где любое действительное число. Нормируя, получаем  ; ; . Следовательно, .

Для третьего собственного числа имеем систему:

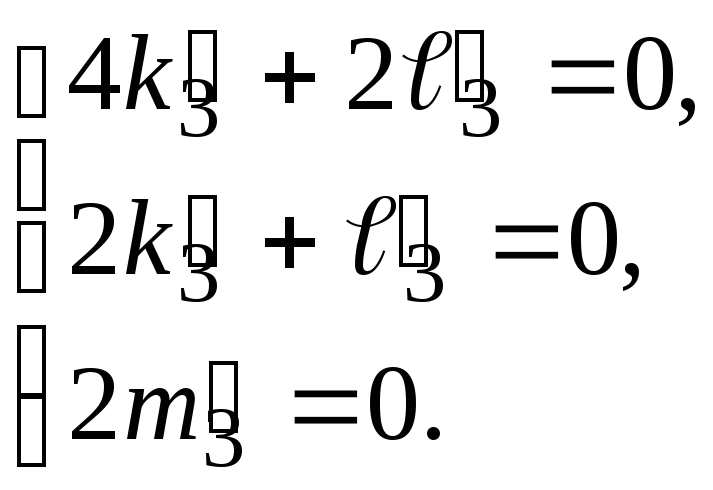
Отсюда , , , где – любое действительное число. Нормируя , находим , , , т.е. вектор . Таким образом, собственные векторы квадратичной формы: , , , а каноническая форма квадратичной формы: .