§2. Разложение определителя по элементам столбца (строки). Теорема о чужих дополнениях

Определение 1. Дополнительным минором некоторого элемента а_ij квадратной матрицы А порядка n, называется определитель D_ij матрицы порядка n – 1, которая получается из данной матрицы А вычеркиванием i-ой строки и j-го столбца (пересекающихся на этом элементе).

Пример. 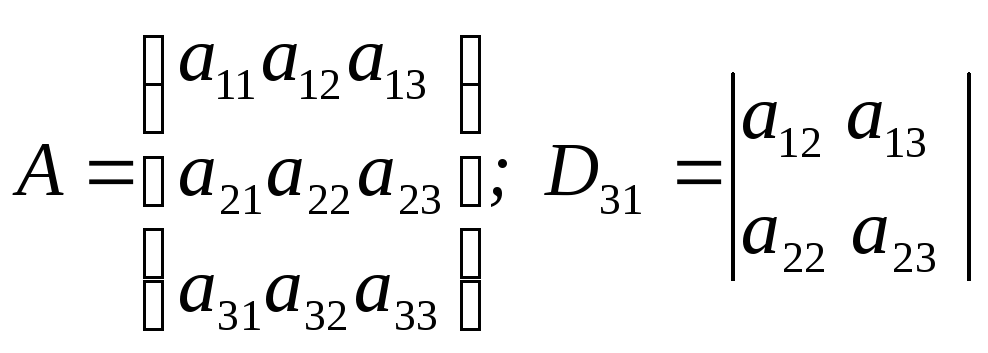– дополнительный минор элемента а₃₁.

Определение 2. Алгебраическим дополнением А_ij элемента а_ij называется его дополнительный минор D_ij умноженный на (–1)^i+j

А_ij = (–1)^i+j· D_ij

Справедливо следующее утверждение, которое мы примем без доказательства: если элементы некоторой строки (столбца) умножить на их алгебраические дополнения и эти произведения сложить, то получится величина определителя.

Данные разложения позволяют вычисление определителя порядка n свести к вычислению n определителей порядка n – 1. Кроме этих формул часто бывает, полезна и следующая теорема.

Теорема (о чужих дополнениях). Если элементы некоторой строки (столбца) умножить на алгебраические дополнения соответствующих элементов другой строки (столбца) и эти произведения сложить, то сумма будет равна нулю.

a_ij , где j = 1,2,...,n – элементы i-ой строки, а А_кj, где j = 1,2,...,n алгебраические дополнения элементов к-ой строки.

Доказательство. Рассмотрим определитель матрицы В, которая получается из матрицы А заменой элементов к-ой строки на элементы i-ой строки. Поскольку это определитель с двумя равными строками, то он равен нулю

Заметим, что в_кj = а_ij, а В_кj = А_кj, тогда , что и требовалось доказать.

Пример. .

Теперь дадим геометрическую интерпретацию определителю.

§3. Геометрическое представление определителя

Рассмотрим упорядоченную тройку некомпланарных свободных векторов и поставим им в соответствие упорядоченную тройку направленных отрезков исходящих из одной точки в ориентированном пространстве. На этих направленных отрезках, как на сторонах, построим параллелепипед (рис.2.6).

Имеется бесконечное множество ориентированных параллелепипедов, каждому из которых ставится в соответствие та же упорядоченная тройка векторов. Эти параллелепипеды получаются переносами любого из них и имеют, поэтому один и тот же объем V_p. Если вектора компланарны, то объем такого вырожденного параллелепипеда принимается равным нулю.

у

Z

С

В

D А

х

Рис. 2.6

Определим объем V_p параллелепипеда, построенного на векторах , в координатах. Для этого выберем в пространстве ортонормированный базис связав с ним систему координат x, y, z (рис.2.6). И пусть относительно этого базиса три вектора заданы своими координатами:

.

Введем две операции над свободными векторами.