3.1. Типы векторов в геометрическом пространстве
Определение 1. Два направленных отрезка равны, если выполнены следующие условия:
-
начало отрезков находятся в одной и той же точке;
-
длины отрезков равны;
-
отрезки принадлежат одной прямой;
-
направленные отрезки имеют одинаковые направления.
Если
для установления равенства векторов
основываться на данном определении,
тогда для любого вектора представленного
направленным отрезком
–
равным ему будет вектор, который
изображается тем же направленным
отрезком
.
Вектора, удовлетворяющие этому правилу,
называются связанными
векторами.
Связанные вектора отображаются
единственным направленным отрезком, и
другого направленного отрезка равного
этому вектору не существует.
Определение 2. Два направленных отрезка равны, если выполнены следующие условия:
1) длины отрезков равны;
2) отрезки принадлежат одной прямой;
3) направленные отрезки имеют одинаковые направления.
Если для установления равенства векторов основываться на данном определении, тогда множество направленных отрезков расположенных на одной прямой и имеющие одинаковую длину и направление (отложены они могут быть из любой точки этой прямой) отображают равные вектора, а, следовательно, один и тот же вектор, такое множество равных между собой (в смысле определения 2) направленных отрезков называется скользящим вектором.
Определение 3. Два направленных отрезка равны, если выполнены следующие условия:
1) длины отрезков равны;
2) направленные отрезки имеют одинаковые направления;
3) направленные отрезки коллинеарны.
Если для установления равенства векторов основываться на данном определении, тогда множество направленных отрезков, расположенных на одной прямой или на параллельных прямых, имеющие одинаковую длину и направление, отображают равные вектора. Такое множество равных между собой (в смысле определения 3) направленных отрезков называется свободным вектором.
Свободный
вектор
обозначают и изображают любым из
направленных отрезков
того множества направленных отрезков,
которое является вектором
.
В каждой точке пространства А'
всегда можно построить направленный
отрезок
,
принадлежащий множеству направленных
отрезков данного вектора
(т.е.
=
)
и этот направленный отрезок для конкретной
точки А'
будет единственным. Эту операцию
осуществляют при помощи параллельного
переноса.
В дальнейшем будем рассматривать лишь свободные вектора, и называть их, по мере возможности, просто векторами. Это связано с тем, что на свободные вектора накладывается наименьшее число ограничений, и все остальные вектора представляют собой частный случай свободных векторов, на которые накладываются дополнительные ограничения.
3.2. Векторное пространство свободных векторов над полем R
На множестве свободных векторов в геометрическом пространстве зададим две операции – сложение векторов и умножение на число из поля R. Покажем, что с этими операциями множество свободных векторов образует векторное пространство над полем R.
Сложение
свободных векторов.
Пусть даны два свободных вектора
и
.
Построим равные им направленные отрезки
и
(это
можно сделать для любой точки В
пространства). Тогда направленный
отрезок
,
принадлежащий множеству направленных
отрезков вектора
,
называется суммой векторов
и
и обозначается
+
.
Заметим, что все три вектора
,
и
+
=
принадлежат одному и тому же множеству
свободных векторов, т.е. сложение есть
внутренний закон композиции. Выясним
его свойства.
1.
Сложение векторов коммутативно, т.е.
+
=
+
.
Действительно, отложим вектор
от произвольной точки А:
=
,
а от точки В
отложим
вектор
:
=
.
Тогда
+
=
.
Отложим теперь сначала от точки А
вектор
:
=
.
Тогда в силу равенства
=
(четырехугольник
АВСD
– параллелограмм) имеем
,
т.е.
есть
вектор
,
отложенный от точки D.
Таким образом,
+
=
+
=
и поэтому
+
=
+
.
2.
Сложение векторов ассоциативно, т.е.
для любых векторов
,
и
выполнено
Доказательство.
Пусть А
– произвольная точка, а В,
С,
D – такие
точки, что
тогда
,
.
-
,
т.е.
–
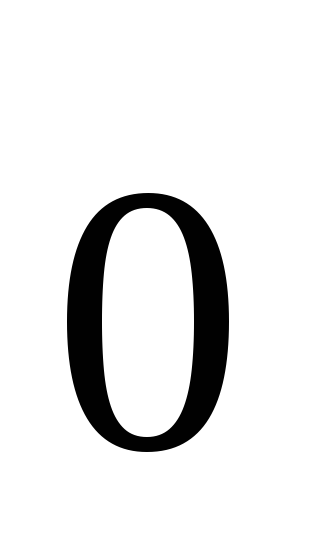нейтральный
элемент. -
,
–
симметричный элемент.
Последние два свойства очевидны. Таким образом, сложение на множестве свободных векторов составляет абелеву группу.
Умножение
свободного вектора на число из
R.
Произведением
числа
R
на свободный вектор
в случае
,
,
называется вектор, коллинеарный вектору
,
модуль которого равен
и который направлен в ту же сторону, что
и вектор
,
если
и в противоположную, если
.
Если
=
или
=
,
то по определению
=
.
Из
определения вытекает следующее условие
коллинеарности
векторов: если два вектора
и
связаны
соотношением
=
,
то эти вектора коллинеарны. Такие вектора
называются пропорциональными.
Таким образом, умножение вектора на число R представляет собой внешний закон композиции. Определим его свойства.
1.
Для любых чисел R
и R
и любого вектора
.
-
1·
=
,
= 1 – нейтральный элемент умножения в
R. -
Для любых чисел R и R и любого вектора
.
-
Для любых векторов
и
и
любого числа R
.
Первые
три свойства очевидны. Докажем свойство
4. Предположим, что векторы
и
не
коллинеарны. Случай коллинеарности
векторов
и
сводится к свойствам 3 и 2. Отложим вектор
от точки А:
а вектор
от точки В:
.
Построим векторы
и
(рис.2.3).
Рис. 2.3