5.1. Обратная матрица

Рассмотрим матрицу А, которая задает отображение Обратное отображение существует, если это взаимно однозначное отображение Рⁿ на Рⁿ. Но для этого необходимо и достаточно, чтобы матрица А была квадратной порядка n и ранг r(A) которой равен n. Поэтому обратная матрица существует только для квадратной матрицы А ранг r(A) и порядок n которой одинаковы.

Определение. Квадратная матрица, представляющая обратное отображение для матрицы А, называется обратной матрицей для матрицы А и обозначается А^-1; матрица А^-1 является симметричным элементом для матрицы А относительно умножения.

Действительно, пусть задано взаимно однозначное отображение пространства Рⁿ на Рⁿ. Обратным отображением для него будет , поэтому А^-1А = Е_n; точно так же АА^-1 = Е_n и, следовательно, АА^-1 = А^-1А = Е_n. Если А^-1 существует, то говорят, что матрица А обратима. Обратно, если А – обратимая матрица, то отображение взаимно однозначно.

Пусть А и В – две обратимые матрицы порядка n; в силу ассоциативности

АВВ^-1А^-1 = А(ВВ^-1)А^-1 = АЕ_nА^-1 = (АЕ_n)А^-1 = АА^-1 = Е_n.

Следовательно, (АВ)(В^-1А^-1) = Е_n, а значит, произведение двух обратимых матриц – есть матрица обратимая и (АВ)^-1 = В^-1А^-1.

5.2. Транспонированная квадратная матрица.

Симметрические матрицы

Определение 1. Говорят, что матрица А^Т элементов транспонирована по отношению к квадратной матрице А элементов , если = , для i = 1,2,...,n; j = 1,2,...,n.

А = , А^Т = .

Элементы матрицы А^Т симметричны элементам матрицы А относительно главной диагонали. Операция, переводящая квадратную матрицу в ее транспонированную, называется транспонированием. Для этого элементы каждой строки матрицы А записываются в том же порядке в столбцы матрицы А^Т, причем номер столбца совпадает с номером строки. Ясно, что при этом i-ая строка А^Т состоит из тех же элементов, в том же порядке, что и i-й столбец матрицы А.

Матрицы А и А^Т имеют одинаковый ранг r(A) = r(A^Т), а также:

(А)^Т = ^Т; (А+В)^Т = А^Т+В^Т; (АВ)^Т= В^ТА^Т; если А обратима, то (А^-1)^Т = (А^Т)^-1.

Определение 2. Квадратная матрица А элементов _ij называется симметрической, если А = А^Т. В этом случае _ij = _ji, т.е. элементы матрицы А симметричные относительно ее главной диагонали равны друг другу. Все диагональные матрицы симметрические, например, Е = Е^Т.

Упражнения

1. С помощью элементарных преобразований определить ранги матриц:

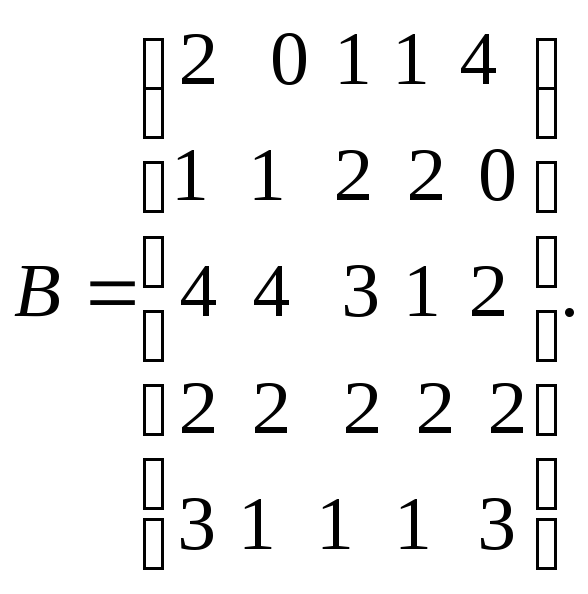
2. Доказать, что для любой матрицы А матрицы S₁= A+A^Т и S₂ = A·A^Т

всегда являются симметрическими матрицами.

3. Пусть Найти С = А + В + А^Т – В^Т + 2АВ.

4. Являются ли матрицы перестановочными.

Глава 6 определители

§1. Определение и свойства определителя, вытекающие из определения

Определение. Рассмотрим векторное пространство квадратных матриц А порядка n над полем P. Зададим такое отображение D пространства этих матриц в поле Р, при котором каждой квадратной матрице

ставится в соответствие число D(A) из P по закону

(6.1)

Это число называют определителем (детерминантом) матрицы А. Обозначение D(A) или |A|.

Из данного определения следует, что отображение D представляет собой числовую функцию, заданную на множестве квадратных матриц, и поэтому роль переменного в ней играет квадратная матрица А. Таким образом, определитель, т.е. значение D(A) числовой функции D, можно рассматривать как числовую характеристику квадратной матрицы А. Порядок матрицы называется и порядком определителя, которой он соответствует.

Сумма в правой части равенства берется по перестановкам вторых индексов элементов матрицы a_ij, где j = 1, 2,...,n. Это означает, что каждой перестановке вторых индексов m₁, m₂,...,m_n чисел 1, 2,...,n, или соответствует слагаемое. Каждое слагаемое состоит из произведения n элементов, взятых по одному и только одному элементу из каждой строки и каждого столбца. Произведения складываются со знаками определяемые числом инверсий  f) соответствующих перестановок Число таких слагаемых равно числу перестановок 1,2,....,n, т.е. n!.

Примеры. 1.

Действительно, перестановок  m₁,m₂  из 1,2 всего две

2. а₁₁а₂₂а₃₃ –

– а₁₂а₂₁а₃₃ + а₁₂а₂₃а₃₁ – а₁₃а₂₂а₃₁ + а₁₃а₂₁а₃₂ – а₁₁а₂₃а₃₂. Перестановок m₁, m₂ , m₃ из 1, 2, 3 всего 3! = 6.

Свойства определителя, вытекающие из определения:

1. Определитель транспонированной матрицы равен исходной: D(A^T) = D(A). Вытекает из равноправия строк и столбцов по отношению к определителю.

2. Если поменять местами два столбца (строки) определителя, то определитель изменит знак на противоположный. Действительно, если столбцы (строки) меняются местами, то это приводит к транспозиции в перестановке а транспозиция, как мы установили, приводит к изменению четности перестановки (книга 1, гл.2, § 2, п.3). Следовательно, все слагаемые определителя изменят знак на противоположный.

3. Определитель, у которого две строки (столбца) одинаковы, равен нулю. В самом деле, если в определителе переставить две одинаковые строки (столбца), то, с одной стороны, мы ничего не изменим, а с другой стороны, в соответствии с п.2, изменим знак определителя на противоположный, т.е. D(A) = – D(A), отсюда D(A) = 0.

4. Если все элементы столбца (строки) определителя умножить на одно и то же число, то и определитель умножится на это число.

Таким образом, если все элементы некоторой строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.

5. Если каждый элемент какого-либо столбца (строки) есть сумма двух слагаемых, то определитель равен сумме двух определителей, у которых столбцами (строками) являются соответствующие слагаемые, а остальные совпадают со столбцами (строками) заданного определителя:

Свойства 4 и 5 вытекают из дистрибутивности умножения относительно сложения. Свойство 5 можно рассматривать, как правило для сложения определителей.

Следствия. 1. Величина определителя не изменится, если к элементам какого-либо столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число.

2. Если А – матрица порядка n, то D(A)=ⁿ D(A).

3. D(A)·D(B)=D(A·B). Даже если A·B  B·A, то, тем не менее

D(A·B) = D(A)·D(B) = D(B·A).