
- •25.1. Общие положения 103
- •27.1. Общие положения 116
- •31.1. Общие положения 140
- •1.2. Центральное проецирование
- •1.3. Параллельное проецирование
- •2.1. Инвариантные свойства параллельного проецирования
- •2.2. Прямоугольное (ортогональное) проецирование
- •2.1. Инвариантные свойства параллельного проецирования
- •2.2. Прямоугольное (ортогональное) проецирование
- •3.3. Коэффициенты искажения
- •3.4. Виды аксонометрических проекций
- •4.2. Прямоугольная изометрическая проекция
- •4.3. Прямоугольная диметрическая проекция
- •4.4. Косоугольная фронтальная диметрическая проекция
- •5.1. Комплексный чертеж точки
- •5.2. Проекции прямых общего положения
- •5.1. Комплексный чертеж точки
- •5.2. Проекции прямых общего положения
- •6.2. Проекции проецирующих прямых
- •6.3. Определение натуральной величины отрезка прямой общего положения
- •6.4. Деление отрезка прямой в данном отношении
- •7.2. Пересекающиеся прямые
- •7.3. Скрещивающиеся прямые
- •8.1.1. Проекции плоскостей уровня
- •8.1.2. Проекции проецирующих плоскостей
- •8.1.1. Проекции плоскостей уровня
- •8.1.2. Проекции проецирующих плоскостей
- •9.1. Взаимное расположение двух плоскостей
- •9.2. Пересечение плоскостей общего положения
- •9.1. Взаимное расположение двух плоскостей
- •9.2. Пересечение плоскостей общего положения
- •10.2. Пересечение прямой линии с плоскостью
- •10.3. Условие видимости на чертеже
- •11.2. Прямая, перпендикулярная к плоскости. Теорема о проецировании прямого угла
- •12.1. Перпендикулярные плоскости
- •12.2. Перпендикулярные прямые
- •12.1. Перпендикулярные плоскости
- •12.2. Перпендикулярные прямые
- •13.2.1. Падающая тень от точки
- •13.2.2. Падающая тень от прямой линии
- •13.2.3. Тень от плоской фигуры
- •13.2. Тени от точки, линии и плоской фигуры
- •13.2.1. Падающая тень от точки
- •13.2.2. Падающая тень от прямой линии
- •13.2.3. Тень от плоской фигуры
- •13.2.4. Тень от диска (окружности)
- •14.1. Тень, падающая от одной фигуры на другую
- •1. Метод обратных лучей
- •14.1. Тень, падающая от одной фигуры на другую
- •14.1.1. Метод обратных лучей
- •2. Метод следа светового луча (метод сечения лучевой плоскостью)
- •15.1. Тени геометрических тел
- •15.1.1 Тени многогранников
- •15.1.2. Тени цилиндра
- •15.1.3. Тени конуса
- •15.1. Тени геометрических тел
- •15.1.1 Тени многогранников
- •15.1.2. Тени цилиндра
- •15.1.3. Тени конуса
- •16.1. Тени пересекающихся многогранников (от здания)
- •Тени пересекающихся многогранников (от здания)
- •17.1. Тени на фасадах зданий
- •17.1.1. Построение теней в нишах
- •Тени на фасадах зданий
- •17.1.1. Построение теней в нишах
- •Тени от выступов
- •18.2. Замена плоскостей проекций
- •19.1. Вращение вокруг оси, перпендикулярной плоскости проекций.
- •19.2. Плоскопараллельное движение.
- •19.1. Вращение вокруг оси, перпендикулярной плоскости проекций
- •19.2. Плоско-параллельное движение
- •20.1.1. Винтовая линия
- •20.2. Поверхности
- •20.2.1. Поверхности линейчатые
- •20.2.2. Поверхности линейчатые развертывающиеся
- •20.2..3. Поверхности линейчатые неразвертывающиеся
- •20.2.4. Поверхности нелинейчатые
- •20.2.5. Поверхности параллельного переноса, вращения и винтовые
- •21.1. Поверхности вращения
- •21.2.Поверхности винтовые
- •21.1. Поверхности вращения
- •21.2. Поверхности винтовые
- •22.2. Пересечение плоскостью поверхности вращения
- •23.3. Конические сечения.
- •23.3. Конические сечения
- •24.2. Пересечение прямой с поверхностью многогранника
- •24.3. Пересечение прямой с поверхностью вращения
- •25.2. Пересечение многогранников
- •25.3. Способ секущих плоскостей
- •Пересечение поверхностей
- •26.2. Способ эксцентрических сфер
- •26.3. Особые случаи пересечения. Теорема Монжа
- •27.2. Аналитический способ
- •27.3. Способ триангуляции (треугольников)
- •27.4. Способ нормального сечения
- •28.1. Способ раскатки
- •28.2. Приближенные построения разверток
- •28.1. Способ раскатки
- •28.2. Приближенные построения разверток
- •Список рекомендованой литературы к разделам 1‑9
- •Введение в черчение
- •29.1. Инструмент и материал
- •29.2. Форматы
- •29.3. Масштабы
- •30.3.1. Порядок заполнения основной надписи
- •30.2. Шрифты чертежные
- •Основная надпись
- •Порядок выполнения основной надписи
- •30.3.1. Порядок заполнения основной надписи
- •31.2.1. Построение касательной к окружности
- •31.2. Построение касательных и касание окружностей
- •31.2.1. Построение касательной к окружности
- •31.2.2. Касание окружностей
- •31.2.3. Построение касательных к двум окружностям
- •Сопряжения с помощью дуги окружности
- •31.2.4. Сопряжение двух прямых дугой окружности
- •31.2.5. Сопряжение дуги и прямой дугой окружности заданного радиуса
- •31.2.6. Сопряжение двух дуг дугой окружности заданного радиуса
- •32.1.Вычерчивание контуров деталей
- •32.2. Архитектурные обломы
- •32.1.Вычерчивание контуров деталей
- •32.2. Архитектурные обломы
- •33.1 Циркульные кривые
- •33.1.1 Завитки
- •33.2. Коробовые кривые
- •33.3. Лекальные кривые
- •33.3.1. Порядок вычерчивания лекальных кривых
- •33.3.2. Способы построения некоторых лекальных кривых
- •34.1. Правила и рекомендации при простановке размеров нанесение размеров
- •34.1. Правила и рекомендации при простановке размеров
11.2. Прямая, перпендикулярная к плоскости. Теорема о проецировании прямого угла
Прямая, перпендикулярная к плоскости, перпендикулярна к любой прямой этой плоскости. На основании теоремы о проецировании прямого угла, а суть ее в следующем:
при прямоугольном проецировании прямой угол проецируется в натуральную величину (прямым) только в том случае, если одна из его сторон параллельна плоскости проекций, а другая – не перпендикулярна этой плоскости,
в качестве прямых плоскости общего положения удобнее всего использовать ее линии уровня.
Поэтому, проводя перпендикуляр к плоскости, необходимо брать в этой плоскости две такие прямые: горизонталь и фронталь.
Проекции прямой, перпендикулярной к плоскости, на комплексном чертеже перпендикулярны к соответствующим проекциям ее линий уровня, т.е. если прямая линия перпендикулярна плоскости, то ее горизонтальная проекция должна быть перпендикулярна горизонтальной проекции горизонтали, а ее фронтальная проекция – фронтальной проекции фронтали (рис. 67) или соответствующим следам плоскости (рис. 68).
|
|
|
На рис. 69 изображена плоскость общего положения (a b), к которой к которой требуется провести перпендикулярную прямую.

Рис. 69
Проводим в данной плоскости горизонталь h (через точки 1,3) и фронталь v (через точки 1,4) (рис. 69).
Затем из точки 1 проводим прямую n перпендикулярно к горизонтали и фронтали плоскости следующим образом:
n' h' n'' h''
Построенная прямая n (n', n'') является искомым перпендикуляром к плоскости .
План:
12.1. Перпендикулярные плоскости
12.2. Перпендикулярные прямые
12.1. Перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Построение таких плоскостей может быть выполнено двумя путями:
1) плоскость проводится через перпендикуляр к другой;
2) плоскость проводится перпендикулярно прямой, принадлежащей другой плоскости.
На рис. 70 изображены прямая общего положения l и плоскость общего положения (а b). Требуется построить через прямую l плоскость, перпендикулярную к плоскости .

Рис. 70
Для решения задачи необходимо через какую-нибудь точку данной прямой, например, точку М, провести перпендикуляр к плоскости , заданной пересекающимися прямыми a и b.
Проводим в плоскости горизонталь h и фронталь v (рис. 70).
Далее из точки М, взятой на прямой l, опускаем перпендикуляр n, пользуясь рассмотренным выше положением: n' h'; n'' v'', т.е. горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная его проекция – перпендикулярна фронтальной проекции фронтали (рис. 70).
Плоскость (l n), проходящая через прямую n, будет перпендикулярна к плоскости .
12.2. Перпендикулярные прямые
Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.
На рис. 71 изображена прямая l общего положения, к которой требуется провести перпендикулярную прямую.

Рис. 71
Через точку А прямой l строим перпендикулярную к ней плоскость (h v):
l' h'; l'' h'' (рис. 71).
Любая прямая, лежащая в плоскости будет также перпендикулярна к данной прямой l. Поэтому проведем в этой плоскости произвольную прямую t, на которой возьмем произвольную точку, например, точку В (рис. 71).
Соединив точки А и В, лежащие в плоскости , получим прямую n, перпендикулярную к данной прямой l (рис. 71).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
-
Что называется линией наибольшего наклона плоскости?
-
Как определить угол наклона плоскости к фронтальной плоскости проекций?
-
Как отображается на комплексном чертеже взаимная перпендикулярность прямой и плоскости?
-
Сформулировать необходимые и достаточные условия перпендикулярности двух прямых общего положения.
-
При каких условиях перпендикулярны между собой две плоскости общего положения?
-
Как провести плоскость, перпендикулярную к данной прямой?
-
Как провести перпендикуляр из точки на прямую общего положения?
-
Как построить взаимно-перпендикулярные плоскости?
План:
13.1. Основы теории теней
13.2. Тени от точки, линии и плоской фигуры

 Рис.
67
Рис.
67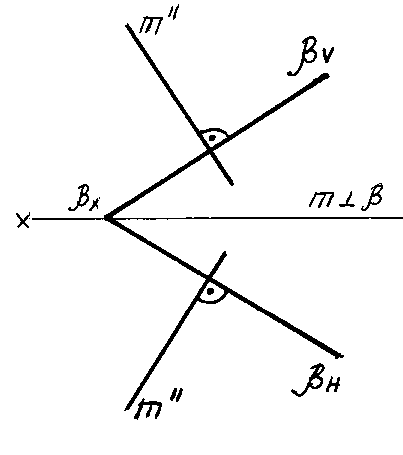 Рис. 68
Рис. 68