3.6. Кут між двома прямими. Кут між прямою і площиною

1. Кут між двома прямими:

і

,

як і кут між двома площинами, визначається кутом між їх напрямними векторами і таким чином:

.

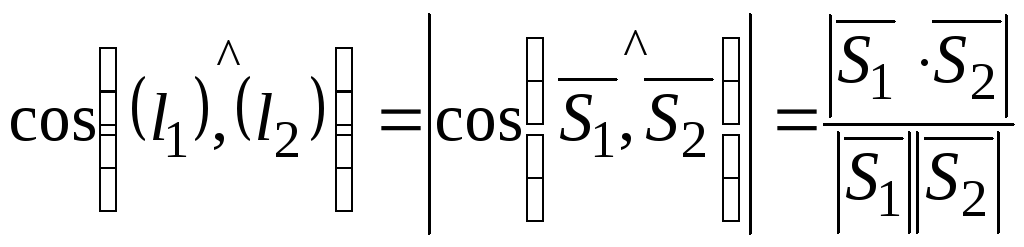Тоді за формулою (2.20) з п.2.5:

. (3.23)

Умовою паралельності прямих є умова колінеарності їх напрямних векторів:

. (3.24)

Умовою перпендикулярності прямих є умова ортогональності їх напрямних векторів:

. (3.25)

2. Кут між прямою і площиною.

Визначається як не тупий кут між цією прямою і її проекцією на площину (кут  на рис.3.10). Нехай площину (Р) задано загальним рівнянням

(Р): ,

а пряму (l) – канонічними рівняннями

.

Якщо напрямний вектор прямої і нормальний вектор площини напрямлені в той самий півпростір відносно заданої площини (Р), то

.

Якщо ж вектори і напрямлені в різні півпростори відносно площини (Р), то

,

тому що . Отже, в усіх випадках . Таким чином кут між прямою (l) і площиною (Р) можна визначити за формулою

. (3.26)

Умовою паралельності прямої і площини є умова ортогональності напрямного вектора прямої і нормального вектора площини:

. (3.27)

Умовою перпендикулярності прямої і площини є умова колінеарності напрямного вектора прямої і нормального вектора площини:

. (3.28)

Приклад 1. Знайти кут між прямими

і

.

Розв’язання. Кут між двома прямими визначається кутом між їх напрямними векторами. Для прямої (l₁) координати напрямного вектора відомі з її канонічних рівнянь: , для прямої (l₂) – з параметричних: .

Тоді за формулою (3.23)

.

Таким чином

.

Приклад 2. Визначити величину кута між прямою

і площиною

.

Розв’язання. Випишемо напрямний вектор заданої прямої (l) . Знаючи крім того нормальний вектор площини (Р), знаходимо за формулою (3.26):

,

звідки

.

3.7. Точка перетину прямої і площини

Нехай пряму (l) задано канонічними рівняннями

,

площину (Р) задано загальним рівнянням

(Р): .

В цьому випадку доцільно переписати рівняння прямої в параметричній формі (3.21):

Точка лежить на прямій (l), при будь-яких значеннях t є поточною точкою прямої. Спільним точкам прямої і площини відповідають ті значення t, при яких координати точки М задовольняють рівняння площини. Для відшукання таких значень підставимо координати точки М у рівняння площини:

.

Розкривши дужки і згрупувавши члени, одержимо:

. (3.29)

Розглянемо існуючі можливості.

а) (нагадаємо, що згідно з (3.27) це означає, що пряма (l) не паралельна площині (Р). В цьому випадку рівняння (3.29) має єдиний розв’язок

,

а точка є спільною точкою прямої (l) і площини (Р), тобто точкою їх перетину.

б) , , тобто згідно з (3.27) пряма (l) паралельна площині (Р), але не лежить у цій площині, тому що координати точки прямої не задовольняють рівняння площини. Рівняння (3.29) у цьому випадку приймає вигляд

,

і не має розв’язків, бо . Пряма та площина не мають точки перетину.

в) , . Це означає, що пряма паралельна площині, а точка прямої лежить у площині, отже і вся пряма (l) лежить у площині (Р). Рівняння (3.29) в цьому випадку має вигляд

,

і задовольняється будь-якими значеннями t (має безліч розв’язків).

Приклад 1. Знайти точку перетину прямої

і площини

.

Розв’язання. Пряму (l) задано канонічними рівняннями. Перепишемо їх у параметричній формі

; ;

і підставимо ці вирази в рівняння площини, щоб визначити при якому значенні t координати точки прямої задовольняють рівняння площини.

.

Розкриємо дужки і зведемо подібні члени:

, звідки t = –1.

Підставляючи це значення у параметричні рівняння прямої, одержимо

; ; .

Отже, пряма (l) перетинає площину (Р) в точці .

Приклад 2. Чи лежить пряма

у площині

?

Розв’язання. Очевидно, що для належності прямої (l) до площини (Р) необхідно виконання двох умов:

а) ортогональність напрямного вектора прямої і нормального вектора площини ;

б) належність хоча б однієї точки прямої до цієї площини.

Перевіримо виконання цих умов.

а) , , отже , тобто .

б) Координати беремо з канонічних рівнянь прямої: . Підставляємо в рівняння площин:

; 0 = 0.

Ми одержали вірну рівність, отже .

Таким чином пряма (l) лежить у площині (Р).