Теоретичні відомості Загальна схема перевірки гіпотез

До проблеми перевірки статистичних гіпотез ми неминуче приходимо в таких часто виникаючих задачах, як порівняльна оцінка різних технологічних процесів за їх продуктивністю та економічністю або порівняння конструктивних особливостей машин, приладів і т.п. Аналогічні задачі характерні для багатьох областей науки та техніки. І хоч критерії перевірки гіпотез досить різноманітні, їх об’єднує загальна логічна схема:

1. Формулюється нульова Н₀ і альтернативна Н₁ гіпотези.

2. Вибирається так званий рівень значущості .

3. Вибирається відповідна гіпотезі статистика критерію Т_n.

4. Знаходиться розподіл статистики Т_n при гіпотезі Н₀.

5. Визначається критична область Y₁ та допустима область Y₁.

6. За вибіркою x₁, x₂, …, x_n обчислюється експериментальне значення статистики Т_n.

7. Приймається рішення про гіпотезу Н₀. Якщо експериментальне значення статистики Т_n потрапляє в критичну область, то гіпотезу Н₀ відкидаємо; в противному випадку говоримо, що вибірка не дає підстави відкинути гіпотезу.

Дамо необхідні пояснення до цієї схеми.

Під статистичними гіпотезами розуміють різного роду припущення про закони теоретичного розподілу. Нульовою (основною) називають висунуту гіпотезу і позначають її символом Н₀. Конкуруючою (альтернативною) називають гіпотезу Н₁, яка суперечить Н₀.

Статистикою критерію Т_n= Т_n(x₁, x₂, …, x_n) називають функцію вибіркових значень, яка використовується для перевірки гіпотез. Статистика Т_n є випадковою величиною, розподіл якої вважається відомим за умови, що нульова гіпотеза Н₀ справедлива.

Основна ідея перевірки статистичних гіпотез

Множину Y всіх значень, які може приймати випадкова величина Т_n, розіб’ємо на дві неперетинаючихся підмножини Y₀ та Y₁ (Y = Y₀  Y₁) так, щоб імовірність попадання значення статистики Т_n у множину Y₁ за умови справедливості гіпотези Н₀ була достатньо малою. Якщо виявилося, що Т_n(x) = Т_n(x₁, x₂, …, x_n)  Y₁, то в припущенні справедливості гіпотези Н₀ трапилась малоімовірна подія, і ця гіпотеза повинна бути відкинутою як така, що протирічить статистичним даним. У протилежному випадку (тобто якщо Т_n(x)  Y₀ ) немає причин не прийняти гіпотезу Н₀, і слід вважати, що спостереження не виявляють протиріч з Н₀.

Найчастіше імовірність попадання у множину Y₁ вибирається рівною або не вищою ніж 0,01 або 0,05 або 0,1. Таку імовірність називають рівнем значущості (); множину Y₁ – критичною областю; Y₀ – областю прийняття гіпотези, а правило перевірки – критерієм згоди.

Якщо Т_n – неперервна випадкова величина, то критична область Y₁ задовольняє рівності:

P{ Т_n  Y₁ | Н₀} =  (7.1)

де вираз у лівій частині позначає імовірність прийняття статистикою Т_n значення у множині Y₁ за умови справедливості гіпотези Н₀.

Зауважимо, що на практиці замість рівності (7.1) часто використовується нерівність (≤) або наближена рівність.

Доцільний вибір критичної області, окрім співвідношення (7.1), може залежати ще й від альтернативної гіпотези Н₁. Найчастіше за критичну область Y₁ вибирають множину:

(правосторонній критерій)

(лівосторонній критерій)

(двосторонній критерій)

де - квантиль рівня  умовного розподілу статистики Т_n (умовного в припущенні справедливості Н₀). Точки, які розділяють множини Y₀ та Y₁, називають критичними точками.

В результаті перевірки статистичних гіпотез можуть бути зроблені помилки двох типів. Помилка першого роду полягає в тому, що буде відкинута вірна гіпотеза Н₀. Її імовірність  дорівнює Р{ Т_n  Y₀ | Н₀}, якщо виконується (7.1). У випадку, коли замість (7.1) виконується нерівність (≤) або наближена рівність, імовірність помилки 1-го роду може бути відповідним чином оцінена, а не точно визначена. Помилка другого роду виникає тоді, коли ми приймаємо гіпотезу Н₀, в той час, коли справедлива альтернативна гіпотеза. Імовірність  помилки другого роду дорівнює Р{ Т_n  Y₁ | Н₁}.

Перевірка гіпотези відносно імовірності

Нехай А – деяка випадкова подія. Маючи результати n незалежних випробувань, в яких подія А спостерігалась m разів, ми хочемо перевірити гіпотезу, що імовірність події А дорівнює заданому числу р₀, тобто Н₀ = { P(A)=p₀ }. На практиці до цієї гіпотези ми приходимо, наприклад, при перевірці відповідності технологічного процесу заданим умовам (наприклад - відсутності систематичної похибки вимірювань).

Нехай гіпотеза Н₀ справедлива. Тоді маємо схему Бернуллі:

успіх – подія А відбулась;

невдача – відбулась подія .

K_n – число успіхів в n випробуваннях;

тоді, як відомо з курсу теорії імовірностей: MK_n=np₀; DK_n=np₀q₀; q₀=1-p₀.

Користуючись нормальним наближенням біноміального розподілу (теорема Муавра - Лапласа), одержуємо:

(7.2)

( статистика Т_n має наближено нормальний розподіл з параметрами 0; 1).

При альтернативній гіпотезі Н₁ ={ P(A)p₀ } і рівні значущості  критична область буде мати вигляд:

(7.3)

(для нормального розподілу U_ =-U_1-, U_ - квантиль рівня  -розподілу). Область прийняття гіпотези у₀ – це інтервал (, ).

Якщо значення статистики Т_n, знайдене за вибірковими даними, належить області Y₀, то гіпотеза Н₀ приймається, в протилежному випадку, коли Т_n Y₁, то гіпотеза Н₀ відхиляється.

Приклад 1. Нехай потрібно перевірити відсутність систематичної похибки терезів, тобто Н₀ = { P(п) = P(н)=p₀=1/2 }, де P(н) - імовірність недоважування, P(п) - імовірність переважування.

В досліді проведено 280 зважувань і із них виявилось 151 недоважувань і 129 переважувань.

При справедливості гіпотези Н₀ маємо р=1/2; q=1/2 і згідно (7.2) одержимо:

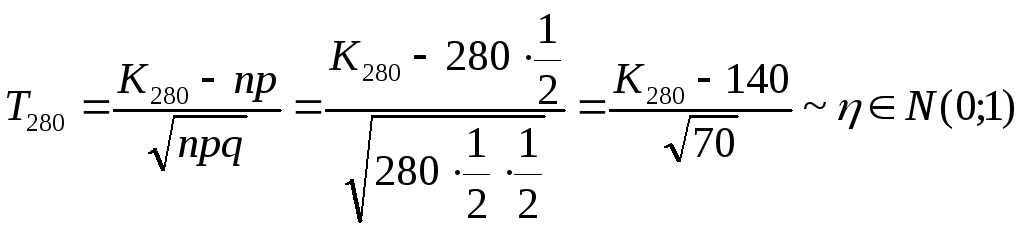Виберемо рівень значущості =0,05, тоді 1-/2=0,975; U_0,975=1,96 – квантиль рівня 0,975 N(0;1)-розподілу. Тоді із рівності (7.3) одержуємо критичну область . Допустима область Y₀ = (-1,96, 1,96).

При кількості успіхів (недоважувань) m=151 отримаємо:

.

Таким чином, Т₂₈₀  Y₀ і гіпотеза Н₀ приймається (Н₀ не суперечить спостереженням).

Зауваження. На практиці наведену вище процедуру перевірки гіпотези відносно імовірностей можна використовувати коли n>=50; np>=10.

Перевірка гіпотези про середнє значення нормального розподілу. Критерій Стьюдента

Нехай x₁, x₂, …, x_n - ряд незалежних спостережень над випадковою величиною , яка має нормальний розподіл N(, ). Параметри  ,  - невідомі. Потрібно перевірити гіпотезу H₀= { M=₀ }, де ₀ – деяке задане число. Такого типу задачі часто виникають на практиці, наприклад тоді, коли потрібно визначити наявність систематичних відхилень від номіналу параметрів виробів деякого технологічного процесу.

На підставі вибірки обчислимо

, (7.3)

Розглянемо статистику

(7.4)

Відомо (див. лаб. роботу № 6), що випадкова величина T_n має розподіл, який називається t - розподілом Стьюдента з (n-1) ступенями волі. Звідси випливає критерій перевірки гіпотези Н₀ – критерій Стьюдента. При рівні значущості  вибираємо із таблиць квантилів t-розподілу Стьюдента - квантиль рівня розподілу Стьюдента з (n-1) ступенями волі.

Тоді при альтернативній гіпотезі Н₁ ={ M₀ } і рівні значущості  критична область відповідно до (7.2) буде мати вигляд:

(7.5)

Допустима область:

.

Якщо статистика T_n в (7.4) при =₀ попадає в область Y₁, то гіпотезу H₀= { M=₀ } відхиляємо, якщо T_n  Y₀, то кажемо, що гіпотеза H₀ не суперечить експериментальним даним.

Приклад 2. Стьюдент у класичній роботі про t – розподіл наводить наступні дані про додаткові години сну 10 пацієнтів, викликані дією снодійних засобів та .

Таблиця 7.1

Пацієнт	X	Y	Різниця X-Y
1	1.9	0.7	1.2
2	0.8	-1.6	2.4
3	1.1	-0.2	1.3
4	0.1	-1.2	1.3
5	-0.1	-0.1	0.0
6	4.4	3.4	1.0
7	5.5	3.7	1.8
8	1.6	0.8	0.8
9	4.6	0.0	4.6
10	3.4	2.0	1.4

Виникає запитання, чи існує істотна різниця між дією снодійних засобів та . Якщо припустити, що різниця ξ між додатковими годинами сну розподілена нормально, то вибірка буде вибіркою об’єму n=10 нормального розподілу N(0, σ) при умові справедливості гіпотези H₀= { M=0 }, тобто коли між снодійними засобами X та Y немає різниці. При цій же умові величина має t – розподіл Стьюдента з 9 ступенями волі; , - відповідно середнє значення та вибіркове середнє квадратичне відхилення вибірки .

Обчислення згідно формул (7.3) та (7.4) для вибірки дають: =1.11; =1.58; .

При α=0.05 та 9 ступенях волі t_кр= =2.26, тоді . Ясно, що і гіпотезу Н₀ відхиляємо, тобто різниця між снодійними засобами та значуща.

Завдання до лабораторної роботи №7

1. Для заданої вибірки x₁, x₂, …, x_n спостережень над випадковою величиною  (див. лаб. роботу №1) перевірити її симетричність відносно середнього значення .

Точніше, гіпотеза полягає в тому, що імовірність прийняття величиною  значення, не більшого від , дорівнює імовірності прийняття нею значення, не меншого від  (таким чином, обидві імовірності дорівнюють 1/2). Скорочений запис:

Нехай: А = {  ≤  };

тоді Н₀ = { P(A)=1/2 },

В якості величини  можна взяти значення .

Перевірку гіпотези Н₀ провести при рівнях значущості =0,05 та =0,1.

2. Для заданої вибірки x₁, x₂, …, x_n спостережень над нормально розподіленою випадковою величиною  (див. лаб. роботу № 6) перевірити гіпотезу H₀= { M=₀ } при рівнях значущості =0,05 та =0,1. За величину ₀ взяти значення ₀ = ( x_min+ x_max )/2.

Контрольні питання до лабораторної роботи №7

1. Дати пояснення основних понять перевірки статистичних гіпотез: основна гіпотеза, статистика критерія, рівень значущості, критична і допустима області, помилки 1-го і 2-го роду.

2. Навести загальну схему перевірки гіпотез.

ЛАБОРАТОРНА РОБОТА № 8

Тема : Перевірка статистичних гіпотез - 2. Гіпотеза про нормальність розподілу імовірностей

Мета роботи : Навчитися перевіряти гіпотези про нормальність розподілу випадкової величини