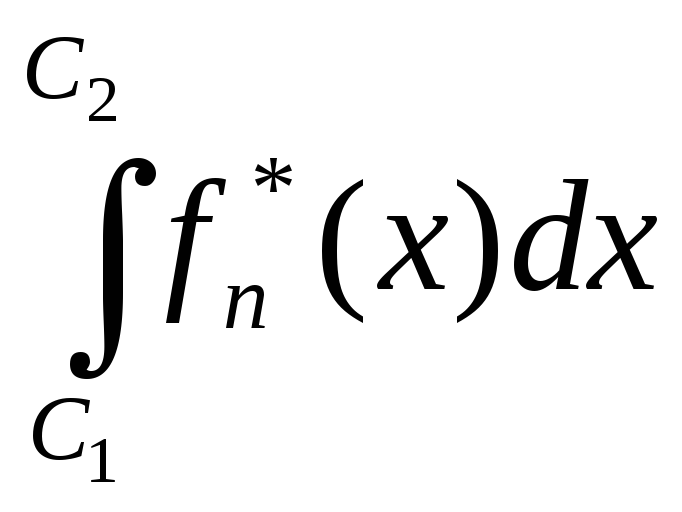ЛАБОРАТОРНА РОБОТА №1

Тема : Способи запису та зображення вибіркових даних

Мета роботи : Навчитися подавати вибіркові дані у компактній формі.

Теоретичні відомості.

Вибірка. Статистичний ряд. “Стеблина з листям”.

Означення. Вибіркою об’єма n будемо називати набір x₁, x₂, …, x_n значень випадкової величини  , які отримані при проведенні n незалежних експериментів. Відзначимо, що якщо експерименти відбулися, то вибірка – це набір конкретних чисел. При цьому в багатьох випадках, наприклад, якщо експерименти тільки повинні відбутися, під вибіркою розуміють набір незалежних випадкових величин, кожна з яких має розподіл досліджуваної випадкової величини .

Розглянемо вибірку, отриману при дослідженні міцності нитки пряжі, записану таблицею:

37	13	25	48	1	36
1	22	31	49	61	48
11	23	34	58	25	48
12	24	36	57	31	57

Така форма запису дає мало інформації про особливості вибірки.

Зобразимо вибірку у вигляді так званої таблиці частот, яку інколи називають статистичним рядом.

Таблиця 1

Таблиця частот

1	11	12	13	22	23	24	25	31	34	36	37	48	49	57	58	61
2	1	1	1	1	1	1	2	2	1	2	1	3	1	2	1	1

У верхньому рядку таблиці записані вибіркові дані, які йдуть по зростанню, у нижньому – частоти, з якими вони зустрічаються у вибірці. Такий запис більш компактний та наочний, хоча багато особливостей і при такому зображенні вибірки залишаються непомітними.

В таблиці 2 вибірку зображено ще у одному вигляді, який називається “стеблиною з листям”. Ліворуч від вертикальної риси записана кількість десятків (“стеблина”), праворуч – одиниці наших чисел (“листя”). Зірочка означає, що до кількості десятків дописується по одній цифрі, які йдуть за вертикальною лінією. З табл. 2 видно, що дана вибірка є групою чисел, яка має майже симетричний характер, з концентрацією в середині вибірки та спаданням на кінцях.

Таблиця 2

“Стеблина з листям”

0*	1	1
1*	1	2	3
2*	2	3	4	5	5
3*	1	2	4	6	6	7
4*	8	8	8	9
5*	7	7	8
6*	1

Доповнимо “стеблину з листям” двома стовпчиками, в першому з яких запишемо кількість елементів у відповідному рядку, а у другому – загальну кількість елементів у цьому та попередніх рядках. Тоді “стеблина з листям” нашої вибірки набуває вигляду:

0*	1	1					2	2
1*	1	2	3				3	5
2*	2	3	4	5	5		5	10
3*	1	2	4	6	6	7	6	16
4*	8	8	8	9			4	20
5*	7	7	8				3	23
6*	1						1	24

З такого рисунку легко знаходити вибіркові елементи за їх рангами (див. розділ роботи “Ранжування вибірки”).

“Стеблина з листям” стає у нагоді при дослідженні вибірок середнього об’єму (50-200 елементів). При цьому способі запису наочно простежуються такі особливості:

• розділяється вибірка на підгрупи чи являє собою одну групу чисел;

• чи симетричне спадання до кінців усередині підгруп;

• чи є більш-менш популярні області;

• чи великий розкид даних та ін.

Ранжування вибірки. Ранг вибіркових елементів

Процес впорядкування вибірки називається ранжуванням. Найчастіше вибірку впорядковують таким чином, що кожний наступний елемент не менше за попередній. Номер елементу x у впорядкованій вибірці називають рангом елементу x і позначають r(x).

При подальших міркуваннях, якщо x₁, x₂, …, x_n – загальна вибірка, то впорядковану вибірку будемо позначати x₍₁₎, x₍₂₎, …, x_(n).

Нехай t – деяке число; [t] – ціла частина числа t; {t} – дробова частина числа t. Визначимо елемент дробового рангу t за формулою:

x_(t)=x_([t])+{t}( x_([t+1])- x_([t]))

Наприклад, елемент x_(6,3) вибірки (табл.2) дорівнює:

x_(6,3)=x₍₆₎+0,3( x₍₇₎-x₍₆₎)=22+0,3(23-22)=22,3.

Медіаною вибірки об’єму n будемо називати вибірковий елемент, ранг якого дорівнює . Медіана позначається або За означенням

Наприклад, медіана вибірки (табл.1) дорівнює:

Нижнім квартилем вибірки називається вибірковий елемент С₁, ранг якого розраховується за формулою: .

Верхнім квартилем вибірки називається вибірковий елемент С₂, ранг якого розраховується за формулою: .

Квартилі разом із медіаною ділять впорядковану вибірку на чотири одинакові за об’ємом частини.

Знайдемо квартилі розглядуваної вибірки (табл.2):

;

;

;

.

“Ящик з вусами”

“Ящик з вусами” – це ще одна з форм (графічна) зображення вибіркових даних. Побудова “ящика з вусами” стане зрозумілою з наступного рисунку, де : x_min=min{x₁, x₂, …, x_n}= x₁; x_max=max{x₁, x₂, …, x_n}= x_n

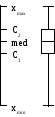
Завдання до лабораторної роботи №1

1. Отримати вибірку згідно своєму варіанту (див. додаток 1 до методичних вказівок).

2. Побудувати таблицю частот для заданої вибірки.

3. Зобразити вибірку у вигляді “стеблини з листям”.

4. Обчислити медіану та квартилі.

5. Побудувати “ящик з вусами”.

Контрольні питання до лабораторної роботи №1

1. Що таке вибірка?

2. Що називається статистичним рядом?

3. Як будувати “стеблину з листям”? Про що можна дізнатися з такого зображення вибіркових даних?

4. Що таке ранг вибіркового елемента? Як знаходити елементи дробового рангу?

5. Прокоментувати графічне зображення вибіркових даних - “ящик з вусами”.

ЛАБОРАТОРНА РОБОТА №2

Тема : Групування вибірки. Полігон і гістограма

Мета роботи : Навчитися проводити первинну статистичну обробку і аналіз даних.

Теоретичні відомості.

Для полегшення аналізу вибірок великого об’єму використовується так зване групування вибірки з наступною побудовою полігонів і гістограм.

Процедура групування полягає в заміні індивідуальних вибіркових значень x₁, x₂, …, x_n деякою сукупністю числових інтервалів (інтервалів групування) [, ], [, ], …, [, ], k>1 та вказівкою, скільки вибіркових значень належить кожному з цих інтервалів. При цьому об’єднання всіх зазначених інтервалів повинно містити в собі всі вибіркові значення x₁, x₂, …, x_n.

Сукупність інтервалів групування і відповідних кількостей вибіркових значень називається згрупованою вибіркою.

Частіше за все використовують інтервали групування однакової ширини. Існують різні методики їх побудови. В даній роботі для групування вибірки пропонується наступна послідовність дій.

1) Визначається наближена кількість інтервалів групування за формулою:

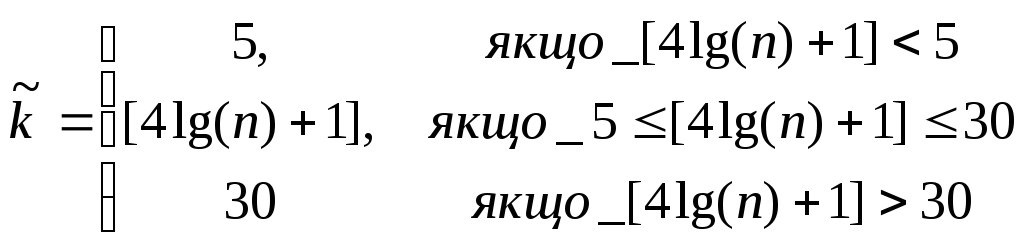, (2.1)

де n – об’єм вибірки; - ціла частина числа .

2) Визначається довжина інтервалу групування за правилом:

, (2.2)

де x_max, x_min – відповідно максимальне та мінімальне вибіркові значення.

Відзначимо, що для спрощення побудови число h як правило заокруглюють.

3) Визначаються числа , , ..., (і тим самим – інтервали групування) за формулою:

,

де i змінюється від 1 до k, а число k визначається з нерівності: . Числа , називаються нижньою та верхньою границями i-го інтервалу групування. За нижню границю першого інтервалу групування можна взяти довільне число, але так, щоб в інтервалі [, ] міcтилось принаймні одне вибіркове значення. Визначимо наприклад наступним чином:

. (2.3)

Означення. Абсолютною частотою i-го інтервалу групування називається кількість вибіркових елементів у даному інтервалі (позначається f_i).

Зауваження. Кінець і-го і початок (і+1)-го інтервалів групування збігаються. Тому, якщо вибіркові значення потрапляють на цей “стик”, то половину із них належить віднести до і-го інтервалу, а іншу половину – до (і+1)-го, тобто абсолютна частота і-го інтервалу може бути дробовим числом.

Означення. Гістограмою (від грецького “гістос” - стовп) абсолютних частот називається фігура, утворена із прямокутників, побудованих на інтервалах групування як на основах, а висота кожного прямокутника дорівнює абсолютній частоті відповідного інтервалу групування.

Означення. Полігоном (від грецьких “полі” – багато, “гон” - кут) абсолютних частот називається ламана, утворена послідовним сполученням на площині точок з координатами , де - середина i-го інтервалу групування, тобто , f_i - абсолютна частота i-го інтервалу групування.

Розглянемо побудову гістограми та полігону абсолютних частот на прикладі вибірки, поданої в вигляді таблиці 1 (див. лабораторну роботу №1). У цій вибірці 24 елементи, тому

;

.

Знайдемо границі інтервалів. За формулою (2.3) маємо:

;

далі отримаємо:

;

; і т.д.

Для побудови полігонів та гістограм зручно попередньо заповнити таблицю “групування - частоти”. Так для нашого прикладу відповідна таблиця має вигляд:

Таблиця 2.1

Таблиця “групування - частоти”

№	границі	інтервалів	середні точки	абсолютні частоти
i	ai	ai+1		fi
1	0,5	10,5	5,5	2
2	10,5	20,5	15,5	3
3	20,5	30,5	25,5	5
4	30,5	40,5	35,5	6
5	40,5	50,5	45,5	4
6	50,5	60,5	55,5	3
7	60,5	70,5	65,5	1

Г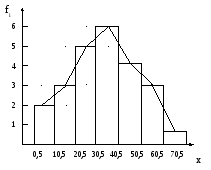істограма та полігон абсолютних частот даної вибірки:

За побудованою гістограмою (полігоном) можна зробити наступні висновки:

а) вибіркові значення лежать в інтервалі від 0,5 до 70,5;

б) найбільш часто зустрічаються значення, що належать інтервалу від 30,5 до 40,5; найбільш рідко – в інтервалі від 60,5 до 70,5;

в) проглядається певна симетричність відносно центральних інтервалів.

Відзначимо, що при аналізі вибірок різного об’єму доцільно використовувати і інші види частот. Наприклад, відносні частоти (при аналізі виборок різного об’єму); приведені частоти (при застосуванні групування з різною шириною інтервалів групування).

Завдання до лабораторної роботи №2

Зауваження.Для виконання роботи використовувати вибірку з лабораторної роботи №1.

1. Заповнити таблицю “групування - частоти” (таблиця 2.1), доповнивши її стовпчиком для значень відносних частот.

2. Побудувати гістограму та полігон абсолютних частот, за якими проаналізувати вибіркові дані.

3. На новому рисунку побудувати гістограму та полігон відносних частот.

4. З даної впорядкованої вибірки утворити нову шляхом відкидання кожного другого елемента. Згрупувати нову вибірку і записати її у вигляді таблиці “групування - частоти”. На рисунках, де побудовані полігони та гістограми початкової вибірки, іншим кольором зобразити полігони та гістограми відповідних частот нової вибірки.

Контрольні питання до лабораторної роботи №2

1. Що розуміють під групуванням вибірки?

2. Що таке абсолютна частота інтервалу групування?

3. Що називається полігоном, гістограмою?

4. Відносні та приведені частоти. Їх гістограми і полігони.

5. Чому побудовані полігони абсолютних частот початкової та побудованої в завданні 4 вибірок сильно відрізняються, в той час як полігони і гістограми відносних частот близькі?

ЛАБОРАТОРНА РОБОТА №3

Тема : Вибіркові аналоги функції та щільності розподілу

Мета роботи : Навчитися оцінювати теоретичні функції і щільності розподілу за допомогою їх вибіркових аналогів

Теоретичні відомості.

Нехай вибірка x₁, x₂, …, x_n - це незалежні спостереження за випадковою величиною  з функцією (теоретичною функцією розподілу).

Нагадаємо, що функцією розподілу випадкової величини  називається функція , x(-; +), яка визначається рівністю:

= P( <x ).

Якщо функція розподілу може бути представлена в вигляді:

де f(x) – деяка невід’ємна функція, то випадкова величина  називається абсолютно неперервною, а для функції f(x) використовується назва щільності розподілу.

Наше завдання полягає в тому, щоб оцінити невідомі функції та f(x), тобто за вибіркою побудувати деякі функції, які будуть наближувати та f(x) при великих об’ємах вибірки n. Такими функціями є емпірична функція розподілу , кумулятивна функція розподілу та гістограма щільностей f_n^*(x).

Емпірична функція розподілу F_n(x)

Означення. Емпіричною функцією розподілу називається функція, яка задається формулою , де К_n(x) – число вибіркових значень х_і таких, що х_і<x, n – об’єм вибірки.

Представимо вибірку у вигляді таблиці частот:

x(1)	x(2)	…	x(m)
n1	n 2	…	nm

де x₍₁₎ <x₍₂₎ <…<x_(m); n_i – кількість повторень елемента x_(і) в вибірці; n₁ +n₂ +…+n_m= n. Тоді побудова графіка функції стає зрозумілою з рисунку 3.1.

Для будь-якого фіксованого х: , тобто прямує до за імовірністю. Це означає, що функція буде обґрунтованою оцінкою для теоретичної функції розподілу .

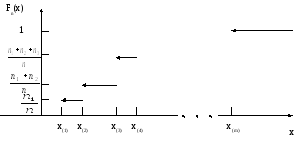
Рис. 3.1

Попередня оцінка функції будувалась за незгрупованою вибіркою. Розглянемо ще одну оцінку для .

Кумулятивна функція розподілу F_n^*(x)

Для згрупованої вибірки за оцінку функції розподілу часто вибирають так звану кумулятивну функцію розподілу , або скорочено - кумуляту (від латинського “кумуляція” - накопичення).

Нехай наша вибірка згрупована у відповідності з завданням №1 лабораторної роботи №2. Для побудови кумулятивної функції розподілу спочатку необхідно знайти абсолютні і відносні кумулятивні частоти. Ці частоти визначаються за формулами:

(3.1)

і=1, 2, ..., k, (3.2)

де f_i – абсолютна частота i-го інтервала групування [a_i, a_i+1]; k – число інтервалів групування. Тоді за означенням:

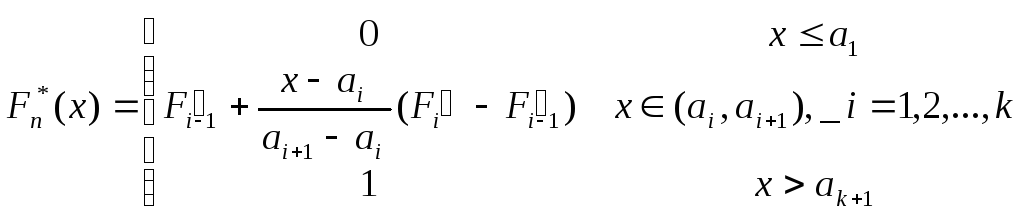(3.3)

, , ..., – границі інтервалів групування.

Іншими словами, для <x< одержуємо, з’єднуючи відрізками прямих точки площини з координатами (, ), i=0, 1, 2,…, k. Графік кумулятивної функції розподілу наведено на рис. 3.3.

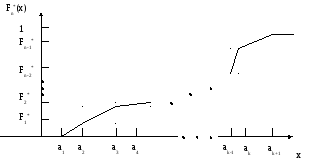
Рис. 3.2

Поряд з кумулятивною функцією розглядають кумулятивну функцію абсолютних частот, яку можна одержати із

рис. 3.2, замінивши відносні кумулятивні частоти на абсолютні кумулятивні частоти та проградуювавши вісь Оу не від 0 до 1, а від 0 до n.

Гістограма щільностей f_n^*(x)

Поряд з абсолютними і відносними частотами розглядаються так звані вибіркові щільності, які визначаються наступним чином:

,

де – абсолютна частота і-го інтервала;

n – об’єм вибірки;

h – довжина інтервалів групування.

Аналітично гістограма щільностей задається наступною формулою:

(3.4)

Гістограма щільностей є оцінкою невідомої щільності розподілу випадкової величини .

З формул (3.3), (3.4) неважко переконатися, що для xa_i, i=1,2,…,k:

а також .

Звідси та з попередніх викладок маємо наступні рівності:

, (3.5)

які дозволяють для великих n наближено знаходити імовірність попадання випадкової величини  в довільний інтервал (, ). Аналогічно, імовірність із співвідношення (3.5) наближено дорівнює також .

Завдання до лабораторної роботи №3

Зауваження.Для виконання роботи використовувати вибірку з лабораторної роботи №1.

1.Для даної вибірки x₁, x₂, …, x_n побудувати емпіричну функцію розподілу .

2. Обчислити абсолютні і відносні кумулятивні частоти згідно формул (3.1) і (3.2).

3. Побудувати графік кумулятивної функції розподілу за даними, згрупованими згідно завдання №1 лабораторної роботи №2.

4. Знайти величини f_n^*(x) і побудувати гістограму щільностей. Обчислити площу області, обмеженої побудованою фігурою.

5. Використовуючи рівності (3.5), знайти наближено імовірність попадання випадкової величини  в інтервал (С₁, С₂), де С₁, С₂ - відповідно нижній та верхній квартилі вибірки. При цьому необхідно провести обчислення величини трьома способами:

а) використовуючи графік емпіричної функції розподілу ;

б) використовуючи графік кумуляти ;

в) використовуючи графік гістограми щільностей f_n^*(x).

Результати обчислень занести в таблицю:

Границі інтерва-лів		Оцінка імовірності попадання випадкової величини в інтервал (С1, С2)
		за емпіричною функцією розподілу			За кумулятою			За гістограмою щільностей
С1	С2	Fn(С1)	Fn(С2)	Fn(С2)- Fn(С1)	Fn*(С1)	Fn*( С2)	Fn*( С2)- Fn*( С1)

Контрольні питання до лабораторної роботи №3

1. Що таке функція розподілу випадкової величини? Сформулюйте її основні властивості.

2. Що таке теоретична функція розподілу?

3. Як за вибіркою оцінити невідому теоретичну функцію розподілу?

4. Що таке щільність розподілу випадкової величини? Сформулюйте її властивості.

5. Що таке теоретична щільність розподілу?

6. Як за вибіркою оцінити невідому щільність розподілу неперервної випадкової величини?

7. Як за вибіркою даної випадкової величини знайти наближено величину ?

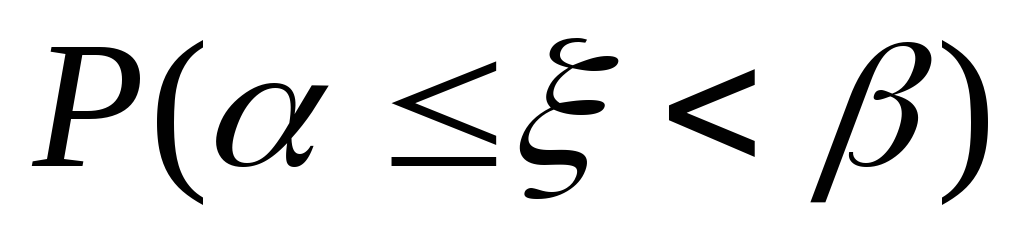8. На якому теоретичному результаті базується можливість оцінки теоретичної функції розподілу емпіричною функцією розподілу?

ЛАБОРАТОРНА РОБОТА №4

Тема : Точкові статистичні оцінки основних числових параметрів випадкової величини

Мета роботи : Навчитися за вибіркою оцінювати основні числові характеристики розміщення, відхилення та форми розподілу частот.

Теоретичні відомості.

При дослідженні випадкових величин часто виникає потреба охарактеризувати випадкову величину за допомогою декількох чисел. Найбільш важливими є числа, що задають:

• центр, навколо якого розсіюються значення випадкової величини;

• відхилення (середнє) випадкової величини від центру розсіювання.

За центр випадкової величини , який є характеристикою її розміщення, найчастіше приймають одне з наступних чисел:

• математичне сподівання випадкової величини М;

• медіану випадкової величини med ;

• моду випадкової величини mоd .

Нагадаємо, що математичне сподівання випадкової величини  - це число, яке обчислюється за однією з формул:

а) - для абсолютно неперервних випадкових величин із щільністю розподілу .

б) - для дискретних випадкових величин, які приймають значення x_i з імовірністю (і=1, 2, ...).

Медіаною (med ) неперервної випадкової величини  будемо називати найменше з чисел х, для яких Р( <x )=0,5. Це означає, що число med  ділить числову вісь на інтервали, в які випадкова величина  попадає з однаковою імовірністю 0,5.

Під модою випадкової величини  будемо розуміти число mоd , яке є:

• точкою максимуму щільності розподілу, якщо  - абсолютно неперервна випадкова величина;

• значенням, яке випадкова величина  приймає з найбільшою імовірністю, якщо  - дискретна випадкова величина.

Зрозуміло, що випадкова величина  може мати декілька мод і що числа М, med  та mоd  не обов’язково рівні між собою, але якщо вони співпадають, то будемо казати, що випадкова величина має симетричний відносно центру (або просто симетричний) розподіл.

Основними параметрами, які характеризують міру відхилення випадкової величини  від центру є дисперсія D та середньо-квадратичне відхилення .

Нагадаємо, що D=М(-М )², а =.

Нехай x₁, x₂, …, x_n - вибірка, отримана при дослідженні випадкової величини , основні числові параметри якої відомі. Потрібно по результатам наших спостережень, тобто по вибірці x₁, x₂, …, x_n , знайти числа, які б були наближеннями невідомих параметрів досліджуваної випадкової величини.

Під точковою статистичною оцінкою невідомого числового параметра  будемо розуміти функцію _n^*= g( x₁, x₂, …, x_n ) вибіркових значень x₁, x₂, …, x_n, яка дає наближення значення параметра , тобто  ~ g( x₁, x₂, …, x_n ) (надалі слово “точкова” часто буде опускатися). Таким чином, для знаходження оцінки числового параметра потрібно підібрати функцію g( x₁, x₂, …, x_n ), яку називають статистикою, значення якої на конкретній вибірці давало б наближення невідомого числового параметра.

Оскільки до початку експериментів вибіркові значення вважаються невідомими і всі вони можуть вважатися випадковими величинами x₁, x₂, …, x_n , то функцію _n^*= g( x₁, x₂, …, x_n ) можна розглядати як деяку випадкову величину _n^*.

Зрозуміло, що для кожного числового параметру треба підібрати свою статистику, більше того, для оцінки одного і того ж параметру можна підібрати різні статистичні оцінки.

Критерії якості точкових статистичних оцінок

Статистична оцінка _n^* параметру  називається незсуненою, якщо М( _n^* ) = .

З двох статистичних незсунених оцінок параметру  ефективнішою називається та, дисперсія якої менше.

Статистична оцінка _n^* параметру  називається обґрунтованою, якщо при оцінка _n^* прямує до числа  за імовірністю, тобто при .

Існує багато методів знаходження точкових статистичних оцінок. Серед таких методів одними з найбільш відомих є метод максимальної правдоподібності (або максимуму правдоподібності) та метод підстановки емпіричного розподілу. Не завжди різні методи дають одні і ті ж рекомендації щодо оцінювання одного і того ж параметру. Втім, обидва названі вище методи призводять до однакової оцінки таких параметрів як математичне сподівання і дисперсія. Нижче наводяться конкретні інструкції відносно оцінювання цих та деяких інших параметрів теоретичного розподілу.

Обчислення статистичних оцінок основних числових параметрів випадкової величини

1. Оцінка математичного сподівання

Для незгрупованої вибірки вибірковим середнім називають статистику . (4.1)

Для згрупованої вибірки вибірковим середнім називають статистику (4.2)

(тут - середні точки інтервалів групування;

- абсолютні частоти цих інтервалів).

Вибіркове середнє використовується як оцінка теоретичного математичного сподівання Мξ. Величина , обчислена за формулою (4.1), є незсуненою обґрунтованою оцінкою Мξ.

2. Оцінка дисперсії та середнього квадратичного відхилення

Для незгрупованої вибірки:

- вибірковою дисперсією називають статистику

; (4.3)

- другим вибірковим центральним моментом називають статистику

(4.4)

Для згрупованої вибірки:

- вибірковою дисперсією називають статистику

; (4.5)

- другим вибірковим центральним моментом називають статистику

(4.6)

де f_i - абсолютна частота,

- середина і-го інтервалу групування;

обчислюється за формулою (4.2) .

Вибірковим середнім квадратичним відхиленням називається статистика . Статистики та є статистичними оцінками середнього квадратичного відхилення  випадкової величини .

3. Оцінка медіани

Для незгрупованої вибірки для оцінки med  розглядається елемент рангу (див. лаб. роботу №1), який називається вибірковою медіаною і позначається med або medх.

Для згрупованої вибірки для знаходження оцінки медіани необхідно знайти абсциссу точки перетину прямої у=0,5 та графіка функції кумулятивних відносних частот (див. лаб. роботу №3). На рисунку 4.1 зображено знаходження медіани для згрупованої вибірки.

Рис.4.1

4) Оцінка моди

Для незгрупованої вибірки за оцінкн моди mоd  приймається вибірковий елемент, що має найбільшу частоту (див. таблицю частот в лаб. роб. №1 ) і позначається mоd.

Для згрупованої вибірки для обчислення моди використовується формула

, (4.7)

де m – номер модального інтервалу групування (тобто того, який містить максимальну кількість вибіркових значень);

h = a_m+1- a_m; d = | f_m-f_m-1 |; d = | f_m+1-f_m |.

Зміст формули (4.1) зрозуміло з рисунку 4.2.

Зауважимо, що якщо f_m-1= f_m= f_m+1, то права частина формули (4.1) не визначена. В цьому випадку покладають:

.

Якщо m=1 або m=k, то у першому випадку покладають f_m-1=0, а в другому f_m+1=0.