§ 12. Функции, измеримые по Лебегу

Литература: [1], глава II, §§ 1-3.

Задачи этого параграфа позволят студенту глубже усвоить понятие измеримой по Лебегу функции на некотором множестве; научиться доказывать различные свойства измеримых функций, используя определение измеримой функции.

Часть задач связывает материал данного параграфа с материалом §11, что поможет осознать связь между измеримостью множеств и измеримостью функций.

208. Выясните, измерима ли функция 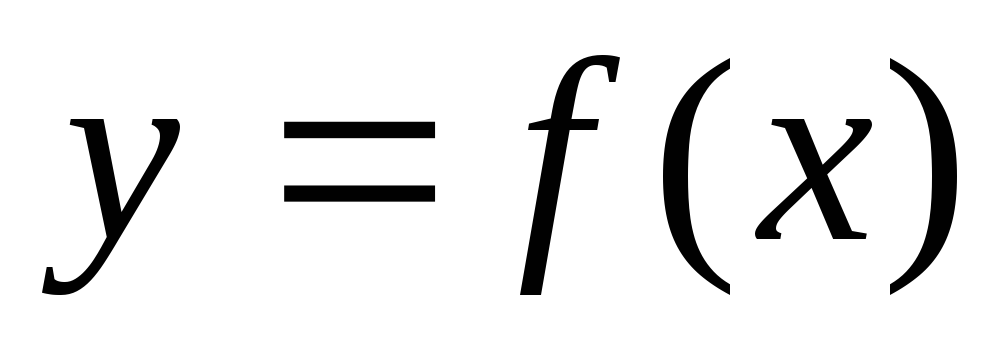на множестве , если функция измерима на этом множестве.

209. Верно ли, что если функция измерима на множестве , то и функция также измерима на этом множестве? Справедливо ли обратное утверждение?

210. Докажите, что если функция измерима на множестве , то и функция также измерима на этом множестве. Верно ли обратное утверждение?

211. Покажите, что если функции и измеримы на множестве , то и функции а) ; б) также измеримы на этом множестве.

212. Следует ли из измеримости функций , и , измеримость функций и ?

213. Докажите, что если функции и измеримы на множестве , то функции

а) ; б)

также измеримы на множестве .

208. Докажите, что если функция измерима на всяком отрезке , то она измерима и на всем отрезке .

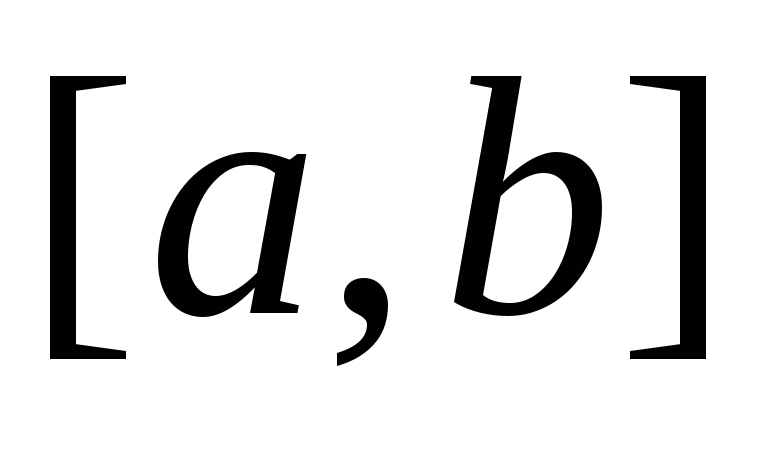209. Докажите, что если функция дифференцируема на отрезке , то производная функция измерима на этом отрезке.

210. Пусть функция 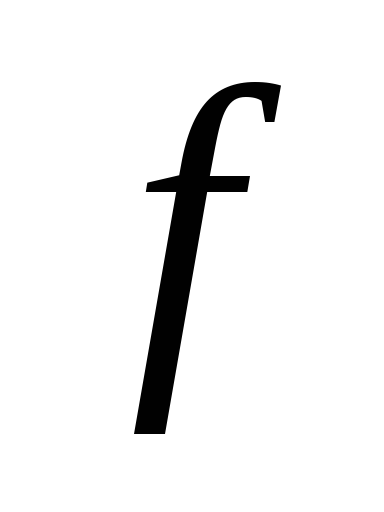измерима на множестве . Выясните, будет ли для произвольно заданных чисел , где , измерима на множестве функция

.

208. Измерима ли функция , равная во всех точках канторова множества и равная во всех остальных точках отрезка ?

209. Пусть 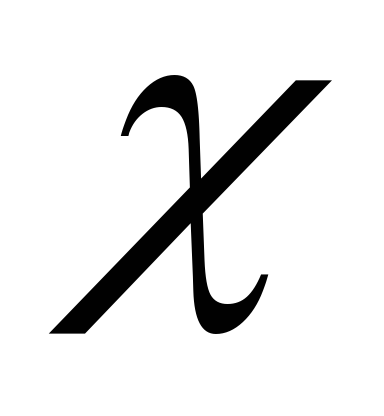– характеристическая функция множества рациональных чисел, то есть . Докажите, что ее произведение на любую функцию есть функция измеримая.

210. Пусть функция измерима на множестве , – произвольное открытое или замкнутое множество на числовой прямой. Докажите, что прообразом множества во всех этих случаях является измеримое подмножество множества .

Дополнительные задания

1. Докажите, что если – измеримое множество, то характеристическая функция измерима. Если же – неизмеримое множество, то – неизмеримая функция.

2. Является ли измеримой функцией сумма сходящегося на отрезке ряда измеримых функций?

3. Пусть – измеримая на множестве функция, – множество ее значений, а – функция, непрерывная на . Выясните, является ли измеримой на множестве сложная функция .

4. Пусть измерима на множестве , 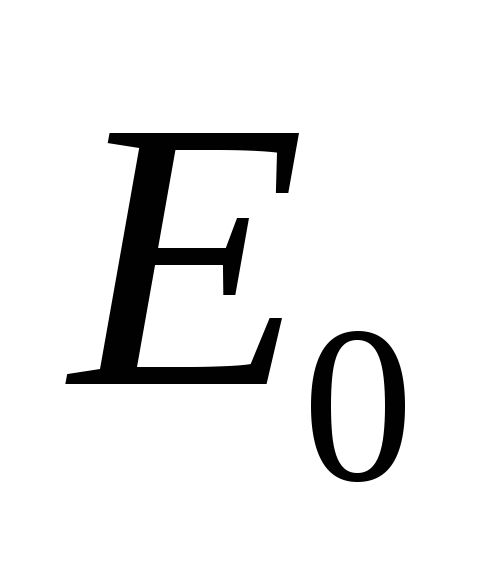– измеримое подмножество множества . Обязано ли множество быть измеримым? Если нет, то приведите соответствующий пример.

5. Пусть – функция, непрерывная на отрезке 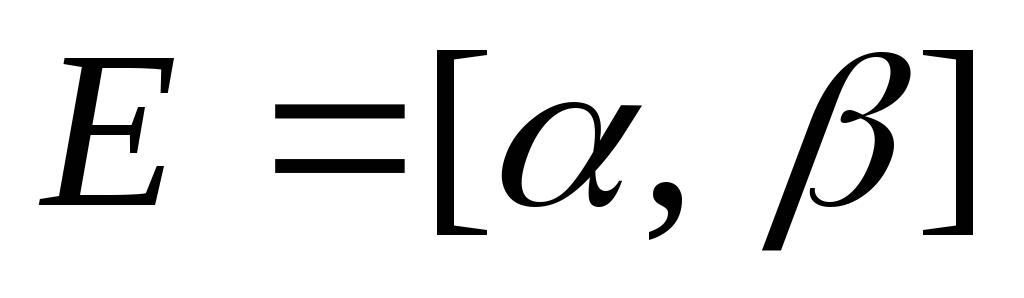, – множество ее значений, а – функция, измеримая на . Обязана ли быть измеримой на множестве сложная функция ?
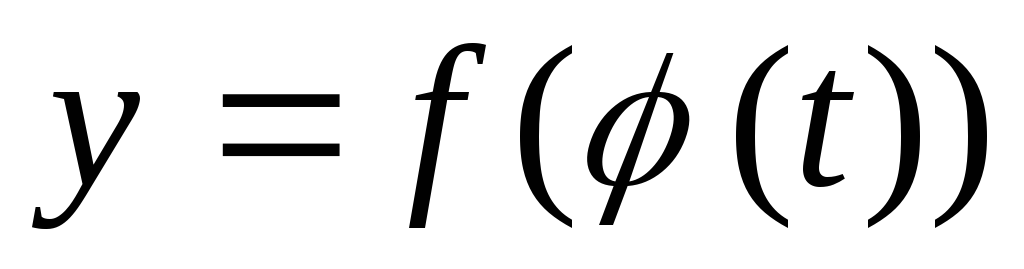