Дополнительные задания

1. Выясните, имеет ли неподвижные точки отображение , заданнное формулой .

2. Выясните, имеет ли отображение , заданное формулой , неподвижные точки.

3. Найдите неподвижные точки отображения .

4. Отображение задано формулой . Найдите неподвижные точки этого отображения.

5. Является ли сжимающим отображение числовой прямой в себя?

6. Покажите, что функция отображает отрезок в себя. Является ли это отображение сжимающим?

7. Докажите, что отображение , заданное формулами не является сжимающим.

8. Докажите, что отображение 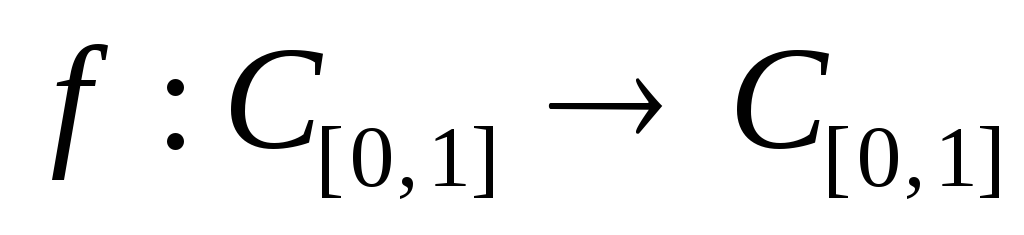, заданное формулой , где , является сжимающим.

9. Пусть – числовая функция, определенная на всем множестве , имеющая производную на R, причем , где К – фиксированное число, . Докажите, что уравнение имеет единственное решение.

§ 11. Измеримые множества

Литература: [1], глава IV, §§1-4;

[5], глава V, § 3.

Задачи настоящего параграфа должны помочь студенту уяснить понятия меры открытого и замкнутого ограниченных множеств, меры Лебега всякого ограниченного множества; понятие измеримого множества в смысле Лебега; изучить свойства измеримых множеств.

189. Докажите, что мера Лебега множества равна двум.

190. Найдите меру множества .

191. Найдите меру Лебега множества решений уравнения .

192. Найдите меру Лебега конечного множества точек.

193. Докажите, что мера Лебега множества, внешняя мера которого равна 0, равна 0.

194. Докажите, что мера Лебега пустого множества равна 0.

195. Найдите меру Лебега множества .

196. Докажите, что мера Лебега всякого счетного множество равна 0.

197. Найдите меру Лебега множества рациональных точек, лежащих на отрезке .

198. Найдите меру Лебега множества иррациональных точек, лежащих на отрезке .

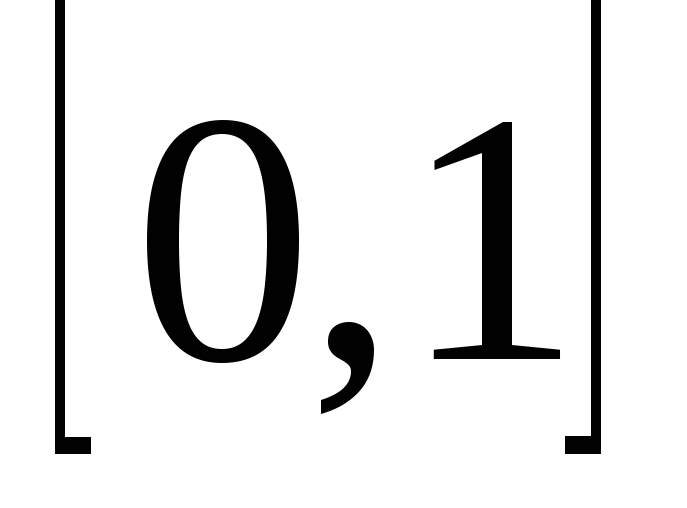199. Докажите или опровергните утверждение: всякое ограниченное открытое множество измеримо по Лебегу.

200. Докажите или опровергните утверждение: всякое ограниченное замкнутое множество измеримо по Лебегу.

201. Найдите меру Лебега области определения функции .

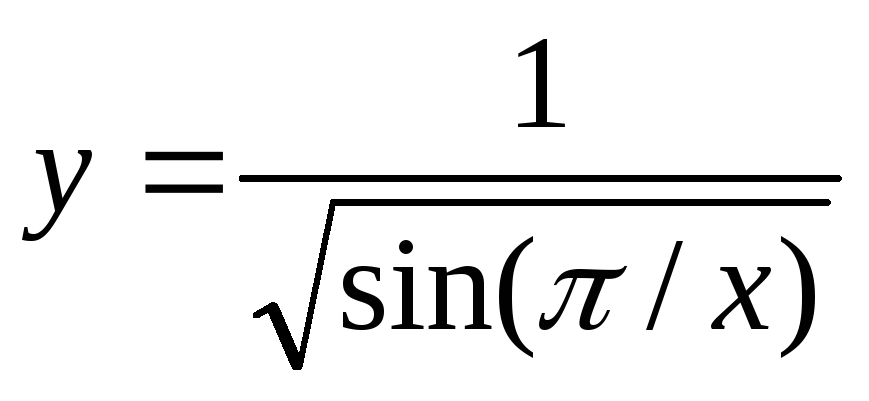202. Докажите, что множество 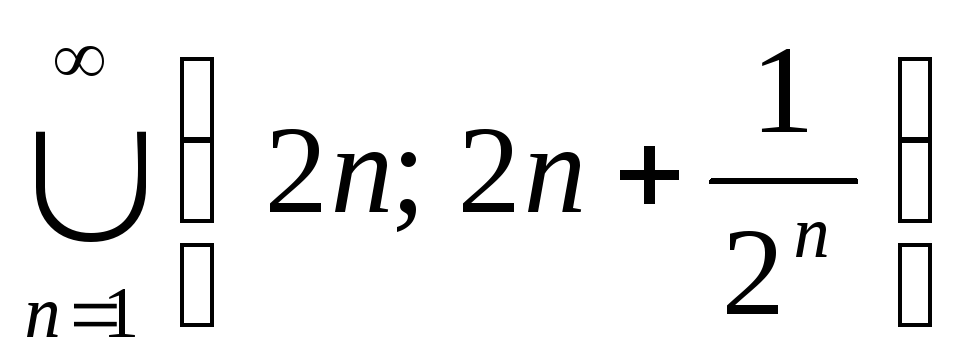измеримо по Лебегу и найдите его меру.

203. Докажите, что объединение двух любых измеримых по Лебегу множеств измеримо по Лебегу.

204. Докажите, что дополнение измеримого по Лебегу множества до измеримого по Лебегу множества измеримо.

205. Докажите, что пересечение двух измеримых по Лебегу множеств измеримо по Лебегу.

206. Докажите, что разность двух измеримых по Лебегу множеств измерима по Лебегу.

207. Выясните, верно ли утверждение: мера Лебега обладает свойством монотонности, т. е., если , то .

Дополнительные задания

1. Докажите, что для измеримости ограниченного множества необходимо и достаточно, чтобы для всякого существовало такое открытое множество , , что .

2. Докажите, что для измеримости ограниченного множества необходимо и достаточно, чтобы для всякого существовало такое замкнутое множество , , что .

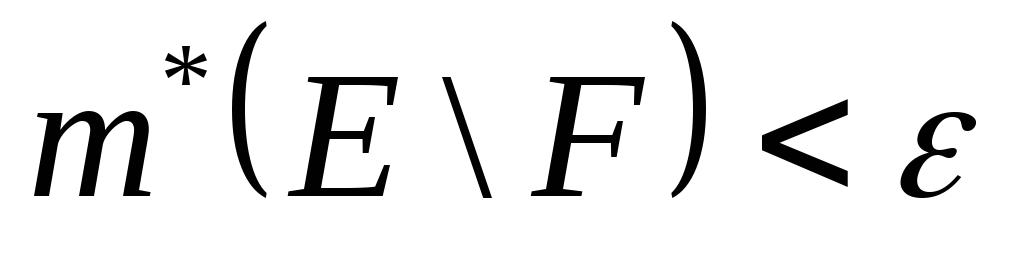3. Докажите, что если A измеримое множество положительной меры, то в нем существуют хотя бы две точки, расстояние между которыми рационально.

4. Множества A и B измеримы по Лебегу, причем . Докажите, что для любого множества верно равенство .

5. Множества A и B измеримы по Лебегу, причем . Докажите, что для любого множества верно равенство .

6. Докажите, что для любых измеримых по Лебегу множеств и справедливо соотношение .

7. Докажите, что множество чисел отрезка , десятичное разложение которых невозможно без цифры 7, измеримо по Лебегу. Найдите его меру.

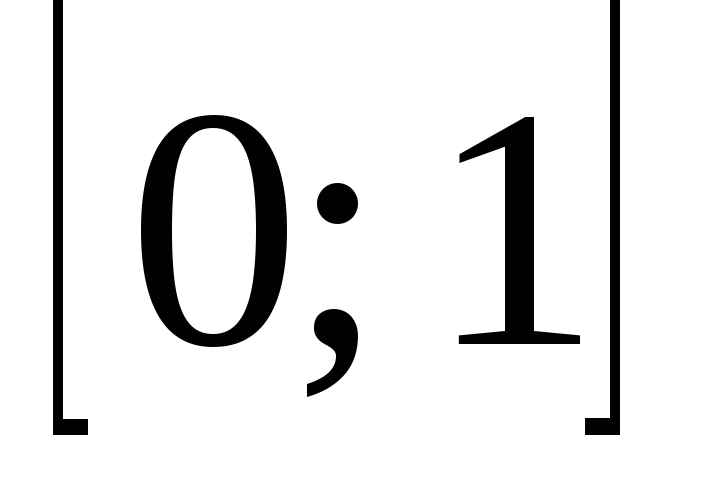8. Докажите, что множество чисел отрезка , десятичное разложение которых не содержит цифры 5, измеримо по Лебегу. Найдите его меру.