Дополнительные задания

1. Выясните, является ли фундаментальной последовательность точек метрического пространства , если ряд сходится.

2. Докажите, что метрическое пространство, состоящее из всех функций, непрерывных на прямой и равных нулю вне некоторого интервала, с метрикой не является полным.

3. Верно ли, что пространство всех функций, имеющих на отрезке непрерывную производную 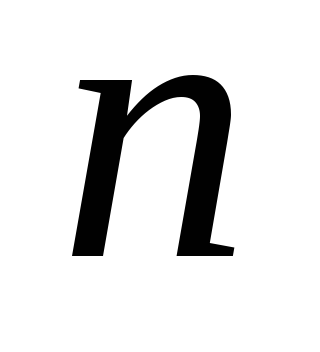-го порядка, с метрикой

является полным?

4. Докажите, что если последовательность точек метрического пространства фундаментальна, то из нее можно выделить такую подпоследовательность , что ряд сходится.

5. Выясните, является ли фундаментальной последовательность функций 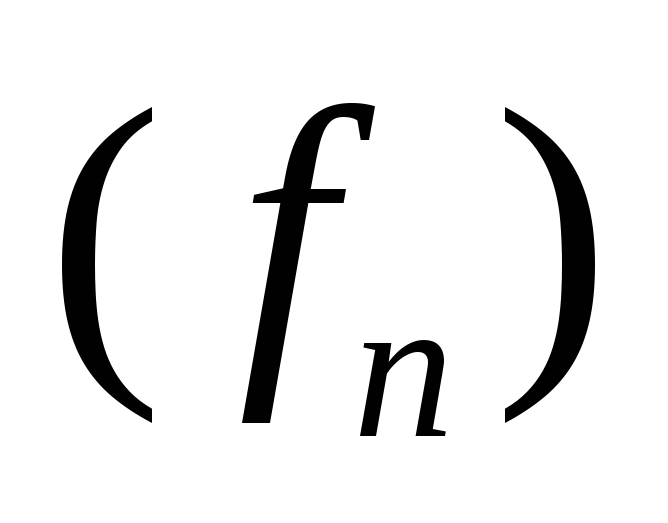, где из пространства функций, непрерывных на отрезке с метрикой .

6. Докажите, что в полном метрическом пространстве всякая последовательность непустых замкнутых вложенных () стягивающихся (последовательность радиусов стремится к нулю) шаров имеет непустое пересечение, состоящее из единственной точки.

7. Верно ли, что подпространство непрерывно дифференцируемых функций пространства 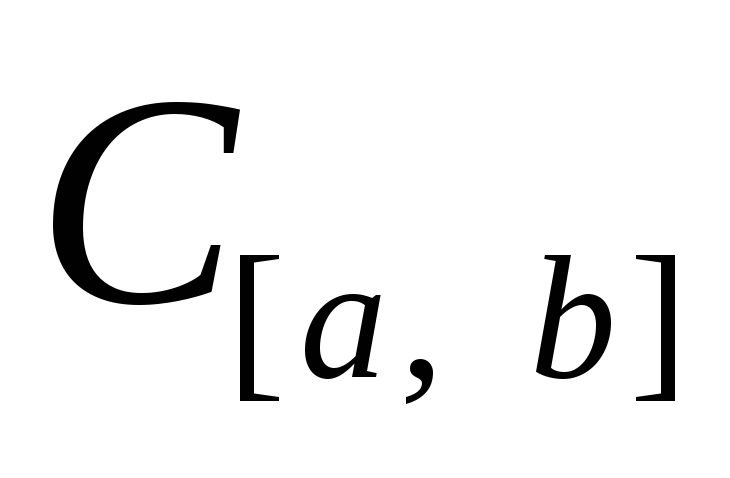является полным?

§ 10. Принцип сжимающих отображений

Литература: [1], гл. XVIII, § 4.

Задачи настоящего параграфа должны помочь студенту уяснить понятие неподвижной точки отображения, его связь с алгебраическими и функциональными уравнениями, решаемыми «методом неподвижной точки»; а также глубже понять условия, при которых отображения оставляют неподвижными некоторые точки рассматриваемых метрических пространств.

171. Найдите неподвижные точки отображения :, заданного формулой:

а) ;

б).

171. Выясните, имеет ли неподвижные точки отображение , заданное формулой: а) ; б).

172. Имеет ли отображение, где E – область определения функции , неподвижные точки?

173. Формулы задают отображение . Найдите его неподвижные точки.

174. Выясните, имеет ли неподвижные точки отображение , заданное формулой: а) ; б) .

175. Выясните, будет ли сжимающим отображение, описанное в задаче 10.173 .

176. Проверьте, что в пространстве формула задает отображение:

а) отрезка ; б) отрезка в себя.

Выясните, будут ли отображения сжимающими.

171. Проверьте, что в пространстве формула отображает отрезок в себя. Будет ли это отображение сжимающим?

172. Выясните, является ли в пространстве сжимающим отображение луча в себя, заданное формулой .

173. Выясните, является ли отображение, описанное в задаче 10.174, сжимающим.

174. Докажите, что отображение 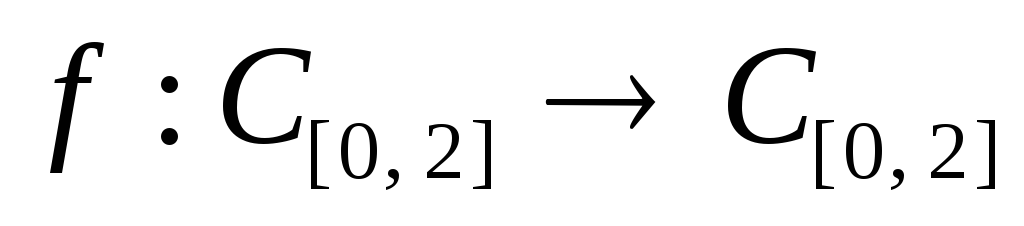, заданное формулой , является сжимающим.

175. Выясните, будут ли сжимающими отображения, описанные в задаче 10.172 .

176. Пусть – полное метрическое пространство и задано отображение . Известно, что для выполняется соотношение . Справедлива ли теорема Банаха для таких отображений?

177. а) Докажите, что если функция отображает отрезок в себя, дифференцируема на этом отрезке и для , то уравнение имеет на единственное решение. б) Будет ли справедливо приведенное утверждение для всей числовой прямой?

178. Докажите, что уравнение имеет на отрезке единственное решение.

179. Для определения точки орбиты, в которой находится спутник в указанный момент времени, приходится решать уравнение Кеплера . Докажите, что при любом и уравнение имеет единственное решение.

180. Отображение, описанное в задаче 10.173, не имеет неподвижных точек. В то же время оно является сжимающим (результат решения задачи 10.176). Нет ли здесь противоречия с теоремой Банаха?

181. На луче задана функция . Покажите, что

а) ;

б) отображение, осуществляемое данной функцией, не имеет неподвижных точек. Нет ли здесь противоречия с теоремой Банаха?