4.3. Регрессионный анализ

Коэффициент корреляции указывает на степень тесноты взаимосвязи между двумя признаками, но он не дает ответа на вопрос, как изменение одного признака на одну единицу его размерности влияет на изменение другого признака. Для того чтобы ответить на этот вопрос, пользуются методами регрессионного анализа.

Регрессионный анализ устанавливает форму зависимости между случайной величиной и значениями переменной величины , причем, значения считаются точно заданными.

Уравнение регрессии – это формула статистической связи между переменными.

Если эта формула линейна, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией (нескольких переменных – множественной)

Если корреляционное поле двух признаков имеет форму, близкую к эллипсу, как на рис. 1,в) и г), то зависимости от и от описываются уравнениями регрессии:

,

где коэффициенты и - коэффициенты регрессии, и - свободные члены уравнения.

Значения неизвестных параметров определяются методом наименьших квадратов из системы:

где  коэффициент корреляции между рассматриваемыми признаками; и  средние квадратические отклонения значений тех же признаков, - средние значения переменных.

Коэффициент регрессии  это величина, показывающая, на сколько единиц размерности изменится величина при изменении величины на одну единицу ее размерности. Аналогично определяется коэффициент .

Как и коэффициент корреляции, коэффициент вариации может принимать и положительные и отрицательные значения. Например, если коэффициент имеет знак "", то это означает, что при увеличении значения признака на единицу его размерности значение признака уменьшается на величину, равную .

Уравнения линейной регрессии являются уравнениями прямых линий в плоскости (рис. 3), проходящих внутри соответствующего корреляционного поля. Такие линии называются линиями регрессии.

П ример 4. По условиям примера 1 определить, как изменяется в среднем масса пловца, если рост увеличится в среднем на 1 см, и построить соответствующую линию регрессии.

Решение. Пользуясь результатами, полученными в примере 1, вычислим коэффициент регрессии:

.

Вывод: если абсолютная поверхность тела увеличится на , то его масса увеличится на 42,74 кг.

Найдем коэффициент для уравнения регрессии:

.

Тогда искомое уравнение примет вид:

.

По этому уравнению строим прямую линию на корреляционном поле (рис.4). Для построения прямой достаточно взять две точки, соответствующие крайним значениям признака :

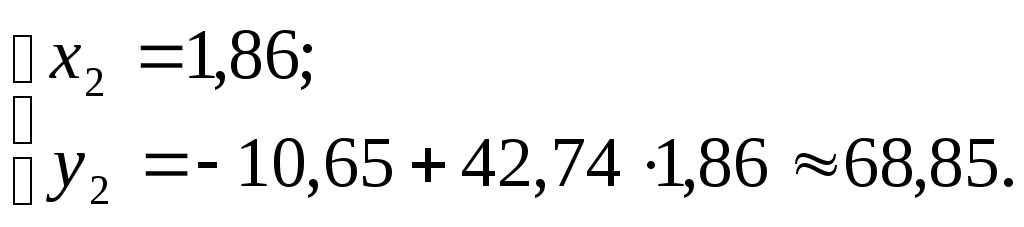
З амечание. По тем же данным можно ответить на другой вопрос: как изменится площадь поверхности тела, если масса спортсмена увеличится на 1 кг? Для этого необходимо вычислить коэффициент регрессии:

.

Это означает следующее: когда вес спортсмена увеличится на 1 кг, абсолютная поверхность тела увеличится на .

Пример 6. Девушки 9-го класса показали результаты в сгибании и разгибании рук в упоре лежа (, раз) и в подтягивании на низкой перекладине из виса лежа (, раз), приведенные в табл.

Требуется:

• определить тесноту взаимосвязи между данными признаками;

• составить уравнение регрессии;

• найти предполагаемый средний результат в подтягивании, если в отжимании показаны результаты: а) 25 раз; б) 6 раз.

, раз	20	14	7	19	7	8	8	12	12	10	10	17	8	12	16
, раз	18	10	5	15	6	10	8	8	8	10	6	10	4	7	10

Решение.

1 . Строим корреляционное поле.

По рисунку видно, что связь между признаками линейная и положительная, так как корреляционное поле представляет собой вытянутый эллипс.

2. Вычисляем тесноту взаимосвязи по коэффициенту корреляции.

В ходе вычислений постепенно заполняем таблицу.

1	20	18	8	9	72	64	81
2	14	10	2	1	2	4	1
3	7	5	-5	-4	20	25	16
4	19	15	7	6	42	49	36
5	7	6	-5	-3	15	25	9
6	8	10	-4	1	-4	16	1
7	8	8	-4	-1	4	16	1
8	12	8	0	-1	0	0	1
9	12	8	0	-1	0	0	1
10	10	10	-2	1	-2	4	1
11	10	6	-2	-3	6	4	9
12	17	10	5	1	5	25	1
13	8	4	-4	-5	20	16	25
14	12	7	0	-2	0	0	4
15	16	10	4	1	4	16	1
	180	135			184	264	188

Вычисляем средние арифметические значения обоих признаков:

, .

Находим произведения и суммируем их (последняя строка в 6-м столбце).

Вычисляем , и суммируем их (последняя строка в 7-м и 8-м столбцах).

Находим средние квадратические отклонения:

, .

Подставляя в формулу вычисленные характеристики, находим коэффициент линейной корреляции : .

3. Проверим достоверность (значимость) полученного коэффициента корреляции.

Для этого вычислим расчетное значение критерия Стьюдента:

.

Задаемся уровнем значимости: . По формуле находим число степеней свободы:

.

Из таблицы критических значений распределения Стьюдента следует:

.

Т.к. , следовательно, коэффициент корреляции значим с вероятностью . Выявлена сильная положительная статистическая взаимосвязь. Это означает, что улучшение результатов в подтягивании связано с улучшением результатов в сгибании и разгибании рук в упоре лежа.

4. Для составления уравнения регрессии находим коэффициенты и :

; .

Тогда уравнение регрессии принимает вид: .

5. Строим линии регрессии на корреляционном поле. Для этого берем две точки, соответствующие крайним значениям признака (можно взять любые другие две точки, удобные для вычислений):

По данным точкам проводим линию регрессии.

П остроенная прямая близка к точкам наблюдений, следовательно, найденное уравнение регрессии имеет хорошее качество и может быть использовано для прогнозирования.

6. Спрогнозируем результат в подтягивании, если результат в отжимании составит а):

.

Так как результат в подтягивании должен быть целым числом, то принимаем: .

При б) имеем:

.

Принимаем .

24