Тема 4. Корреляционный и регрессионный анализ

4.1. Корреляционный анализ

Различные явления и показатели в нашей жизни не являются независимыми, а связаны между собой (цена товара и спрос на него, рост человека и его вес и.т.д.).

Эта зависимость может быть строго функциональной (детермированной) и статистической.

Зависимость между и называется функциональной, когда каждому значению одного признака соответствует одно единственное значение другого признака. (Примером такой однозначной зависимости может служить зависимость площади круга от радиуса).

В реальной действительности чаще встречается иная связь между явлениями, когда каждому значению одного признака могут соответствовать несколько значений другого (например, связь между возрастом детей и их ростом).

Форма связи, при которой один или несколько взаимосвязанных показателей (факторов) оказывают влияние на другой показатель (результат) не однозначно, а с определенной долей вероятности, называется статистической. В частности, если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной.

В зависимости от числа факторов, включаемых в модель, различают парную корреляцию (связь двух переменных) и множественную (зависимость результата от нескольких факторов).

Мы будем рассматривать парную корреляцию (зависимость изучаемого признака от одного признака ).

Корреляционный анализ состоит в определении направления, формы и степени связи (тесноты) между двумя случайными признаками и . В случае, если изучается связь двух признаков, то речь идёт о парной корреляции.

По направлению линейная корреляция бывает положительной (прямой), если при увеличении значений одной переменной увеличивается значение другой, и отрицательной (обратной), если при увеличении значений одной переменной, уменьшается значение другой.

По форме корреляционная связь может быть линейной (прямолинейной), когда изменение значений одного признака приводит к равномерному изменению другого (математически описывается уравнением прямой ), и криволинейной, когда изменение значений одного признака приводит к неодинаковым изменениям другого (математически она описывается уравнениями кривых линий, например гиперболы , параболы и т.д.).

Наиболее простым, приближенным способом выявления корреляционной связи является графический.

При небольшом объеме выборки экспериментальные данные представляют в виде двух рядов связанных между собой значений и . Если каждую пару представить точкой на плоскости , то получится так называемое корреляционное поле (рис.1).

Если корреляционное поле представляет собой эллипс, ось которого расположена слева направо и снизу вверх (рис.1в), то можно полагать, что между признаками существует линейная положительная связь.

Если корреляционное поле вытянуто вдоль оси слева направо и сверху вниз (рис.1г), то можно полагать наличие линейной отрицательной связи.

В случае же если точки наблюдений располагаются на плоскости хаотично, т.е корреляционное поле образует круг (рис.1а), то это свидетельствует об отсутствии связи между признаками.

На рис.1б представлена строгая линейная функциональная связь.

Под теснотой связи между двумя величинами понимают степень сопряженности между ними, которая обнаруживается с изменением изучаемых величин. Если каждому заданному значению соответствуют близкие друг другу значения , то связь считается тесной (сильной); если же значения сильно разбросаны, то связь считается менее тесной. При тесной корреляционной связи корреляционное поле представляет собой более или менее сжатый эллипс.

Количественным критерием направления и тесноты линейной связи является коэффициент линейной корреляции.

Коэффициенты корреляции, определяемый по выборочным данным, называются выборочным коэффициентом корреляции, который вычисляется по формуле:

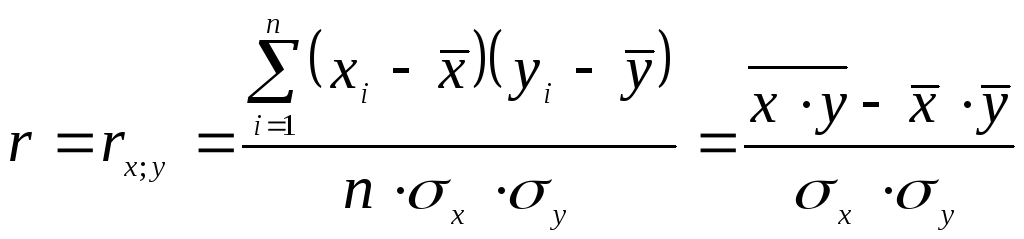
где ,  текущие значения признаков и ; и  средние арифметические значения признаков; 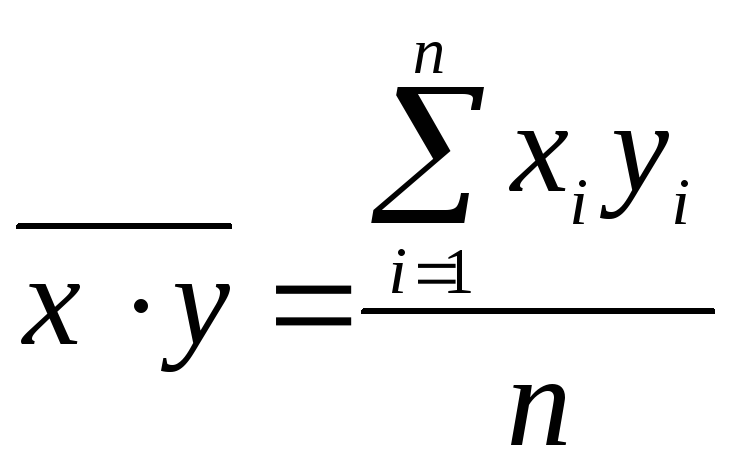- среднее арифметическое произведений вариант, и  средние квадратические отклонения этих признаков;  объём выборки.

Д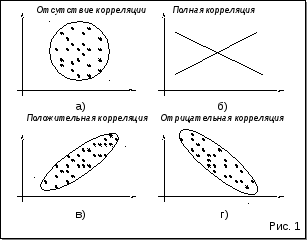 ля вычисления коэффициента корреляции достаточно принять предположение о линейной связи между случайными признаками. Тогда вычисленный коэффициент корреляции и будет мерой этой линейной связи.

Коэффициент линейной корреляции принимает значения от −1 в случае строгой линейной отрицательной связи, до +1 в случае строгой линейной положительной связи (т.е. ). Близость коэффициента корреляции к 0 свидетельствует об отсутствии линейной связи между признаками, но не об отсутствии связи между ними вообще.

Коэффициенту корреляции можно дать наглядную графическую интерпретацию.

Если , то между признаками существует линейная функциональная зависимость вида , что означает полную корреляцию признаков. При , прямая имеет положительный наклон по отношению к оси , при  отрицательный (рис. 1б).

Если , точки находятся в области ограниченной линией, напоминающей эллипс. Чем ближе коэффициент корреляции к , тем уже эллипс и тем теснее точки сосредоточены вблизи прямой линии. При говорят о положительной корреляции. В этом случае значения имеют тенденцию к возрастанию с увеличением (рис.1в). При говорят об отрицательной корреляции; значения имеют тенденцию к уменьшению с ростом (рис.1г).

Если , то точки располагаются в области, ограниченной окружностью. Это означает, что между случайными признаками и отсутствует корреляция, и такие признаки называются некоррелированными (рис.1а).

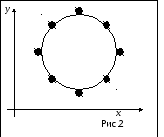
Также коэффициент линейной корреляции может быть близок (равен) нулю, когда между признаками есть связь, но она нелинейная (рис.2).

При оценке тесноты связи можно использовать следующую условную таблицу:

Теснота связи	Величина коэффициента корреляции при наличии
	прямой связи (+)	обратной связи (−)
Связь отсутствует
Связь слабая
Связь умеренная
Связь сильная
Полная функциональная

Пример 1. В таблице приведены значения абсолютной поверхности тела , и его массы , кг у пловцов-перворазрядников.

	1,86	1,76	1,74	1,80	1,68	1,81	1,71	1,80
	69	64	63	67	60	66	63	68

Определить тесноту взаимосвязи между заданными признаками.

Решение. Заметим вначале, что объем выборки . Представим ряды значений графически.

Из рисунка видно, что точки сосредоточены в области, очерченной вытянутым эллипсом, поэтому можно предположить наличие сильной положительной линейной связи между показателями.

Для определения тесноты взаимосвязи воспользуемся коэффициентом линейной корреляции. Для сокращения расчетов будем постепенно формировать таблицу.

1	1,86	69	0,09	4	0,36	0,0081	16
2	1,76	64	-0,01	-1	0,01	0,0001	1
3	1,74	63	-0,03	-2	0,06	0,0009	4
4	1,80	67	0,03	2	0,06	0,0009	4
5	1,68	60	-0,09	-5	0,45	0,0081	25
6	1,81	66	0,04	1	0,04	0,0016	1
7	1,71	63	-0,06	-2	0,12	0,0036	4
8	1,80	68	0,03	3	0,09	0,0009	6
	14,16	520			1,19	0,0242	64

1. Вычислим средние арифметические значения обоих признаков:

, .

2. Найдем отклонения от средних арифметических 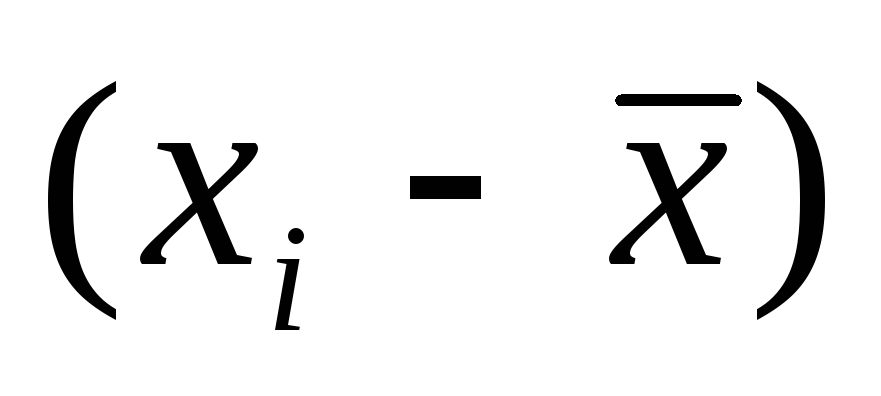и 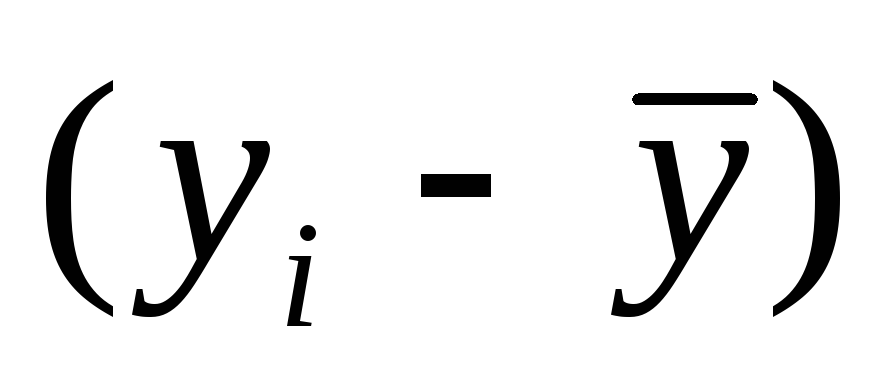и занесем их в 4-й и 5-й столбцы таблицы.

3. Умножим 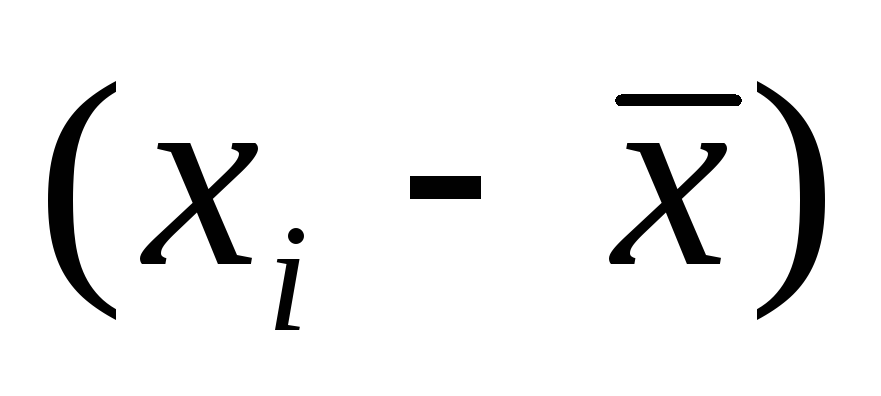на 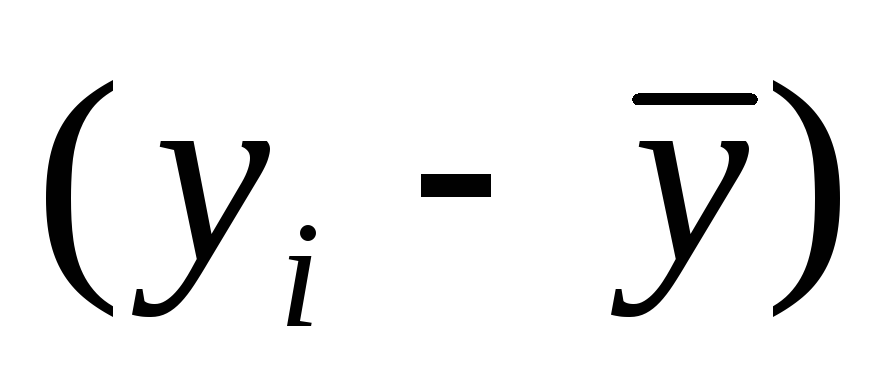и сложим полученные произведения (последняя строка в 6-м столбце).

4. Возведем отклонения в квадрат и сложим (последняя строка в 7-м и 8-м столбцах).

5. Найдем средние квадратические отклонения, пользуясь формулой:

, .

6. Исходя из формулы коэффициента, получим:

.

7. Вывод: полученный коэффициент корреляции указывает на сильную линейную связь между абсолютной поверхностью тела и его массой. Эта связь положительная и означает, что увеличение абсолютной поверхности тела приводит к увеличению его массы и наоборот.

Встречаются задачи, в которых коэффициент линейной корреляции не применим. Это такие задачи, в которых значения признаков не распределены по нормальному закону. Например, такой признак, как место, занятое в данном соревновании, не распределен по нормальному закону. В таких случаях применяют ранговый коэффициент корреляции Спирмена:

,

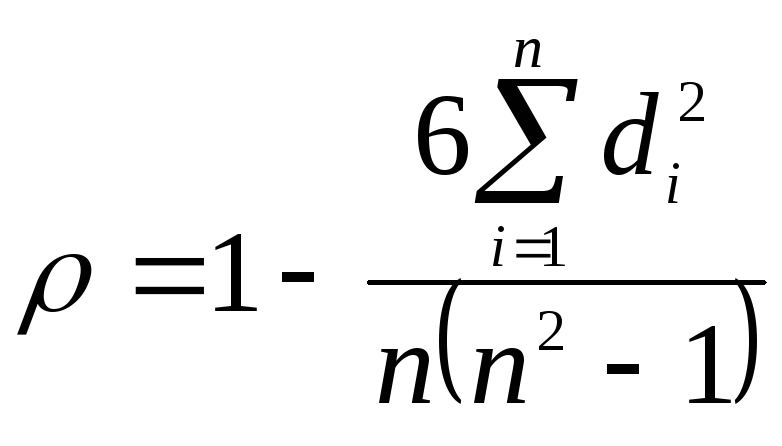где  объем выборки;  разность рангов обоих признаков.

Напомним, что номер признака (в данном примере  место в соревновании) называется рангом.