1.2. Вариационные ряды и их графическое изображение

Задачей статистического описания выборки является получение такого её представления, которое позволяет наглядно выявить вероятностные характеристики.

Различают следующие способы упорядочения данных: по возрастанию, по совпадающим значениям, по интервалам и т.п.

Пусть объём выборки равен n, а число различных значений k (n). Тогда значения признака называются вариантами.

Если значение встретилось в выборке раз, то число называют частотой значения .

Отношение частоты к объёму выборки называется относительной частотой: .

Наблюдаемые значения можно сгруппировать в дискретный статистический ряд:

Х			…
			…
			…

, .

Статистический ряд наглядно можно представить в виде полигона частот (или полигона относительных частот) – ломаной линии, отрезки которой соединяют точки (,) (или (,)).

Пример 1. Анализируется прибыль Х предприятий отрасли. Обследованы 100 предприятий. Данные представлены в виде статистического ряда:

Х	5	10	15	20	25
	5	20	40	25	10
	0,05	0,2	0,4	0,25	0,1

Построить полигон частот.

Решение.

По статистическому ряду можно строить эмпирическую функцию распределения F*(x).

, где - число значений СВ Х< х, - объём выборки.

Свойства F*(x):

1. 0 ≤ ≤ 1.

2. - неубывающая функция, т.е. .

3. .

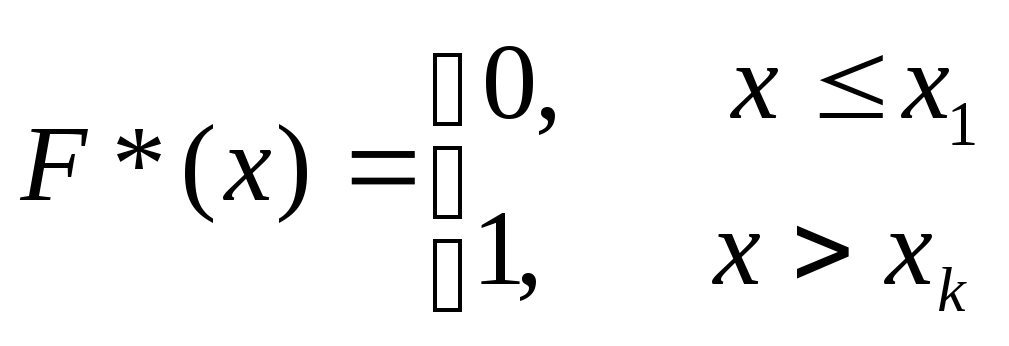Эмпирическая функция распределения является оценкой функции распределения , которая называется теоретической функцией распределения.

При большом объёме выборки (или в случае непрерывного признака) её элементы могут быть сгруппированы в интервальный статистический ряд. Для этого все наблюдаемых значений выборки разбиваются на k непересекающихся интервалов длиной h (- шаг разбиения).

,

где и  соответственно максимальное и минимальное значения признака из выборки.

И находят для каждого частичного интервала частоту - количество наблюдаемых значений СВ Х, попавших в i-й интервал; - относительную частоту (частость) попадания СВ Х в i-й интервал.

Находят накопленные частоты. Накопленная частота -го интервала  это число, полученное суммированием частот интервалов, начиная от первого и заканчивая -м включительно:

.

Находят накопленные частости каждого интервала. Накопленная частость -го интервала  это отношение накопленной частоты к объему выборки:

.

Тогда интервальный статистический ряд имеет вид:

			…
			…
			…
			…
			…

Замечание. Число интервалов часто определяется самим исследователем. Однако лучше всего пользоваться таблицей (см. табл. 1), в которой приведено число интервалов в зависимости от объема выборки.

Таблица 1

Объем выборки n	30  50	50  90	100  200	300  400
Число интервалов k	5 6	7	8	9

Процедура получения интервального вариационного ряда состоит из следующих шагов.

1. Пользуясь табл. 1, находят число интервалов .

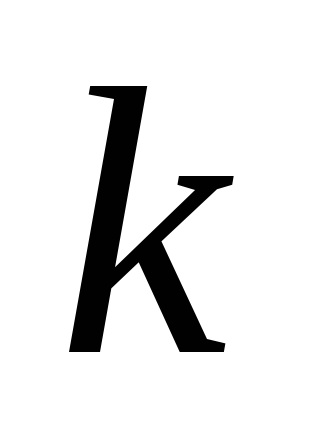2. Определяют длину интервала:

3. Находят границы интервалов.

4. Находят частоты интервалов.

5. Полученные результаты заносят в таблицу.

Интервальный статистический ряд наглядно может быть представлен в виде гистограммы частот – столбиковой диаграммы, состоящей из прямоугольников, основаниями которых служат подынтервалы, а высота равна (плотность частоты). Площадь i-го прямоугольника равна , а площадь всей гистограммы частот равна сумме всех частот, т.е. объёму выборки .

Для построения гистограммы относительных частот основание прямоугольника также равно h, а высота . Площадь каждого столбика равна . Площадь всей гистограммы относительных частот равна .

На основании гистограммы обычно выдвигается предположение о виде закона распределения исследуемой величины.

Пример 2. Анализируется доход населения. Извлечена выборка объёма 300 единиц. По уровню дохода население подразделяется на 6 групп. Данные сгруппированы в интервальный статистический ряд:

	10	50	80	100	40	20

Построить гистограмму относительных частот.

Решение. Шаг h = 20. Разделив относительные частоты на шаг разбиения, получим высоту столбиков.

Форма гистограммы в наибольшей степени соответствует нормальному распределению.

Пример 3. Мальчиками 12  13 лет были показаны следующие результаты в подтягивании на перекладине:

9, 5, 7, 10, 11, 10, 14, 7, 10, 11, 8, 10, 8, 9, 12, 13, 8, 11, 9, 9, 10, 6, 9, 13, 9, 17, 11, 15, 8, 14, 11, 16, 8, 10, 10, 11, 8, 9, 10, 10, 8, 11, 14, 12, 11, 13, 15, 13, 10, 5.

Требуется представить данную неупорядоченную выборку в виде интервального вариационного ряда.

Решение. Непосредственным подсчетом находим объем выборки: .

1. Пользуясь табл. 1, определяем число интервалов. Полагаем .

2. Просматривая заданный ряд, замечаем, что максимальное число подтягиваний равно 17 , а минимальное  5 . Пользуясь формулой, находим длину интервала .

3. Находим границы интервалов.

К границам предыдущего интервала прибавляем длину интервала . В частности,

, .

Замечаем при этом, что правая граница первого интервала является левой границей второго интервала. И так далее до тех пор, пока не найдем: .

4. Считаем частоты каждого интервала, отыскивая в заданном ряду значения, удовлетворяющие неравенству:

, .

В частности, для первого интервала таких значений три, для второго  девять и т. д., то есть

, , , , , .

Полученные данные заносим в таблицу (см. табл. 2, первые три столбца); им же соответствует рис.