8.4 Нормальный закон распределения

Нормальный (гауссовский) закон распределения случайных величин очень удобен для анализа и часто встречается на практике, особенно он характерен для помех канала связи.

Плотность распределения нормальной случайной величины определяется выражением:

,

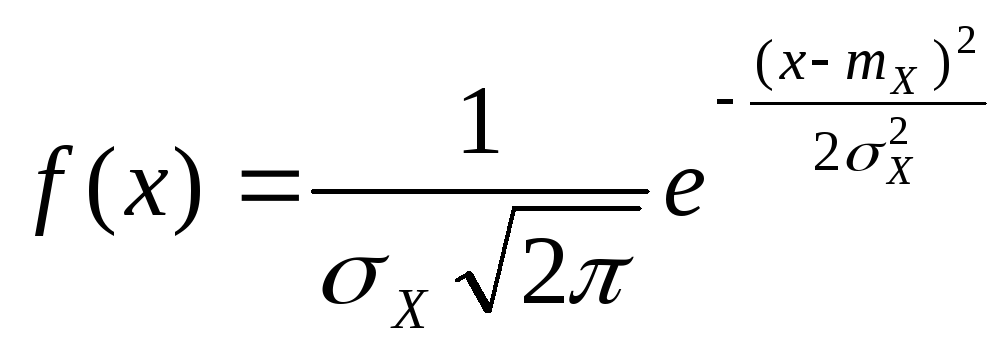где и - соответственно математическое ожидание и дисперсия гауссовской случайной величины.

График имеет симметричный холмообразный вид. Центром симметрии является параметр . Если изменять , кривая распределения будет смещаться вдоль горизонтальной оси, не меняя своей формы. Параметр характеризует форму кривой распределения. При уменьшении максимум увеличивается и кривая все более локализуется в окрестности точки .

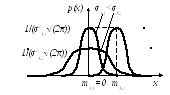
Рисунок 8.4 – Графики случайных величин с нормальным распределением.

График имеет вид монотонной возрастающей от нуля до единицы кривой.

F(x)

1

0,5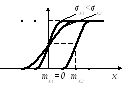

Рисунок 8.5 - Графики случайных величин с нормальным распределением.

9 Сигналы и помехи как случайные процессы

9.1 Основные понятия

Реальные сигналы и помехи являются случайными процессами.

Случайный процесс (СП) – это случайная функция времени, т.е. такая функция времени, значение которой в любой момент времени является случайной величиной. Обозначение: .

Примеры: напряжение шума на выходе линии связи, температура воздуха, ток на выходе микрофона.

Интервал наблюдения – интервал времени, на котором рассматривается СП. Обозначение: , где - длительность интервала наблюдения.

Реализация СП– конкретный вид случайной функции времени, полученный в результате одного наблюдения над СП. Она является уже детерминированной функцией времени. Обозначение: , где - индекс, который указывает на номер наблюдения.

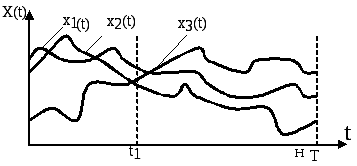
Рисунок 9.1 – Реализации СП.

Ансамбль реализаций СП – совокупность всех возможных реализаций данного СП. Обозначение: . Случайность процесса проявляется в том, что до проведения наблюдения нельзя предсказать, какая именно реализация из ансамбля появится в данном испытании.

Примеры: набор сигналов, наблюдаемых одновременно на выходах многоканальной системы связи; группа сигналов, наблюдаемых одновременно на выходах идентичных генераторов шумового напряжения.

Совокупность значений всех реализаций ансамбля в произвольный момент времени представляет собой случайную величину, называемую сечением СП. Обозначение: .

Для описания случайного процесса применяются следующие статистические характеристики:

- функция распределения вероятности;

- плотность распределения вероятности;

- математическое ожидание;

- дисперсия;

- функция корреляции;

- спектральная плотность мощности.

9.2 Статистические характеристики сп

Функция распределения вероятности и плотность распределения вероятности дают полное вероятностное описание СП лишь для одного фиксированного момента времени .

Функция распределения вероятности определяется как вероятность того, что в момент времени значение СП не превосходит некоторого заданного значения :

.

Плотность распределения вероятности представляет собой производную от функции распределения вероятности:

.

Произведение представляет собой вероятность попадания значения СП в бесконечно малый интервал в окрестности точки .

Математическое ожидание – среднее значение СП в текущий момент времени, полученное усреднением по всему ансамблю реализаций:

.

Дисперсия характеризует среднюю мощность отклонений СП от его среднего значения:

.

Среднеквадратическое отклонение представляет собой квадратный корень из дисперсии и служит амплитудной мерой разброса значений СП в текущий момент времени относительно математического ожидания:

.

Функция корреляция представляет собой меру связи (корреляции) между сечениями СП, взятыми в произвольные моменты времени и :

,

где - двумерная плотность распределения вероятности, которая описывает двумерную случайную величину , образованную совокупностью двух сечений СП в различные моменты времени и ;

- вероятность того, что реализация СП в момент времени попадет в бесконечно малый интервал шириной в окрестности точки , а в момент времени - в бесконечно малый интервал шириной в окрестности точки .

При выражение соответствует определению дисперсии СП.

Чем медленнее убывает функция с ростом интервала между моментами времени и , тем больше промежуток, в течение которого наблюдается статистическая связь между мгновенными значениями СП, и тем медленнее, плавне изменяются во времени его реализации.

Стационарными называют СП, статистические характеристики которых одинаковы во всех временных сечениях. Для стационарного СП функция распределения вероятности, плотность распределения вероятности, математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит не от самих моментов времени, а от интервала между ними . По этой причине при записи статистических параметров стационарного СП можно опускать обозначения фиксированных моментов времени: .

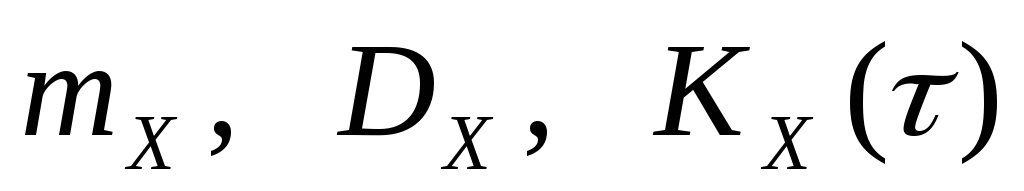Стационарный СП называется эргодическим, если при определении любых его статистических характеристик усреднение по множеству (ансамблю) реализаций эквивалентно усреднению по времени одной, теоретически бесконечно длинной, реализации. Другими словами, если изучаемый процесс является эргодическим, то его реализация достаточной длины является «типичным» представителем статистического ансамбля, и по этой единственной реализации можно определить математическое ожидание, дисперсию и корреляционную функцию СП:

,

,

.

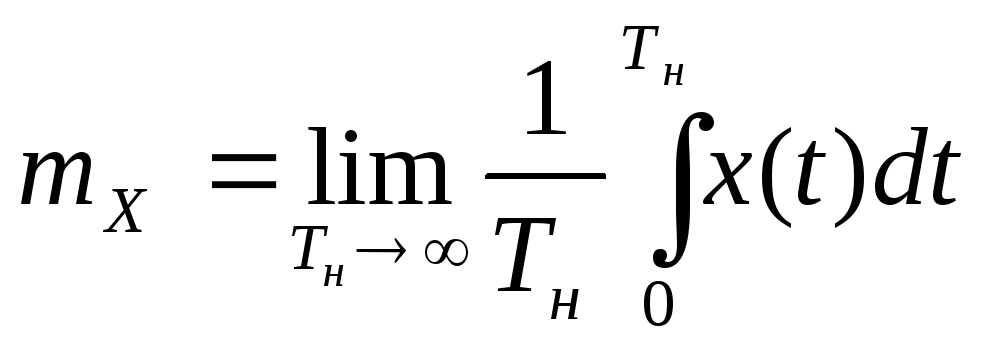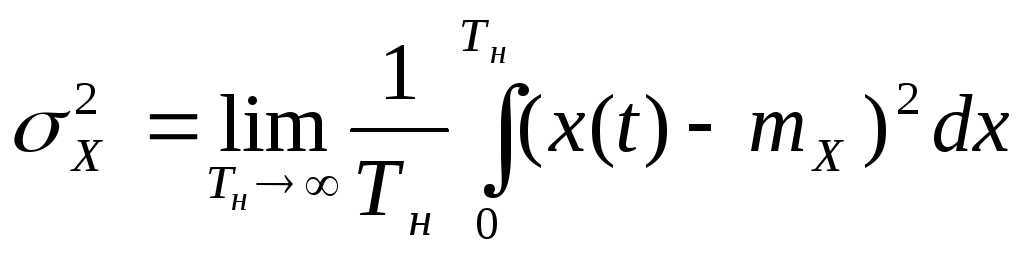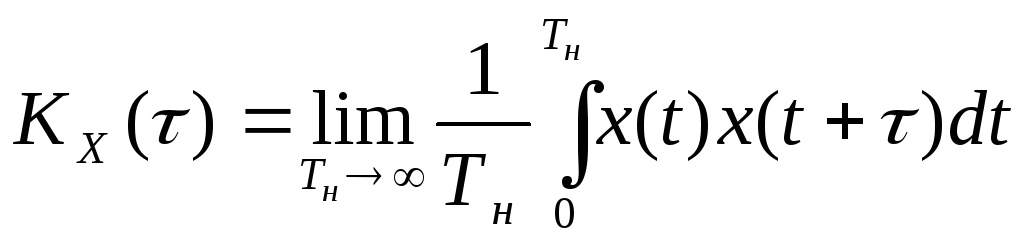где - время наблюдения реализации .

Принято моделировать реальные сигналы эргодическим и стационарным СП.

Спектральная плотность мощности представляет собой среднюю мощность СП, приходящуюся на 1 Гц в окрестности заданной частоты . В общем случае спектральную плотность мощности необходимо усреднить по множеству реализаций, т.е. она находится как среднее значение отношения квадрата спектральной плотности к длительности интервала наблюдения. Если ограничиться рассмотрением эргодических процессов, можно считать, что найденная по одной реализации (путем усреднения во времени) спектральная плотность мощности рассматриваемой реализации характеризует весь процесс в целом:

,

где - спектральная плотность рассматриваемой реализации СП , длительность которой ограничена конечным интервалом . Находится с помощью прямого преобразования Фурье.