
- •Введение
- •1. Основные понятия теории цепей
- •1.1. Основные определения
- •1.2. Идеализированные пассивные элементы
- •Резистивный элемент
- •Емкостной элемент
- •Индуктивный элемент
- •Схемы замещения реальных элементов электрических цепей
- •1.3 Идеализированные активные элементы Схемы замещения источников электрической энергии постоянного тока
- •Управляемые источники тока и напряжения
- •1.4. Топология цепей Схемы электрических цепей
- •Напряжение на участке цепи
- •Закон Ома для участка цепи
- •Компонентные уравнения
- •Законы Кирхгофа
- •Топологические уравнения
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров
- •1.5. Уравнение электрического равновесия цепей Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Классификация электрических цепей
- •2. Методы решения задач определения токов и напряжений.
- •Синусоидальный ток. Основные характеристики.
- •Связанные колебательные контуры общие сведения
- •Схемы замещения
- •Преобразование электрических цепей
- •1.Основные определения
- •Неуправляемые нс Управляемые нс
- •1.Определение рабочих точек нелинейных резистивных элементов.
- •Выпрямление переменного напряжения
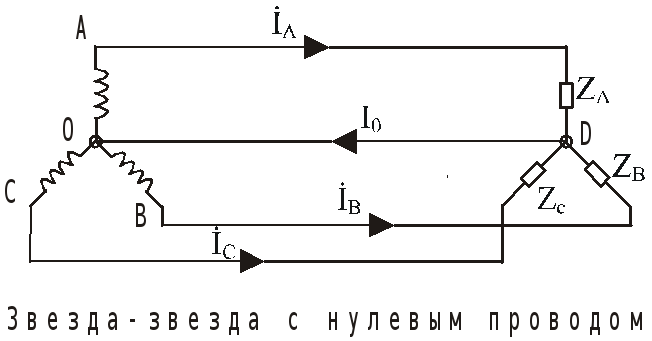
- •Соединение нагрузки в треугольник.
- •Соединение звезда-звезда без нулевого провода.
- •Если нагрузка равномерная, то
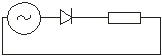
Выпрямление переменного напряжения
Под выпрямителем переменного напряжения понимают процесс преобразования переменного напряжения в постоянное или пульсирующее.
![]()
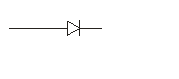


Сопротивление выпрямителя в проводящем направлении в 1000 раз меньше, чем в непроводящем. По числу фаз выпрямленного переменного напряжения выпрямительные схемы делятся на однофазные и многофазные. Однофазные схемы подразделяют на схемы однополупериодного и двухполупериодного выпрямления. В однополупериодных схемах выпрямление производится в течении одного полупериода питающего напряжения, в двухполупериодных – в течении обоих полупериодов.
С(t)
![]()


![]()
Простейшая мостовая схема однофазного двухполупериодного выпрямителя состоит из 4 выпрямителей.
i i Uв Uв e(t) i Rн 1 2 3 4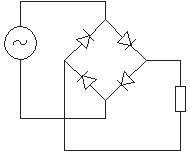

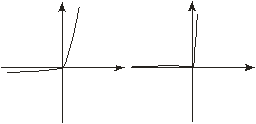
В соответствии с идеализированной ВАХ, когда через выпрямитель проходит ток, падение напряжения на нем равно нулю и, следовательно, сопротивление самого выпрямителя равно нулю. Когда напряжение на выпрямителе отрицательно, т.е. отрицательна взятая в направлении стрелки разность потенциалов на самом выпрямителе, выпрямитель не проводит ток и сопротивление его равно бесконечности.
ωt
Uо ωt
В первый полупериод, когда ЭДС источника положительна и действует согласно с положительным направлением напряжения на выпрямителе, выпрямитель пропускает тон и напряжение на нагрузке равно ЭДС источника. Во второй полупериод, когда ЭДС источника питания отрицательна, выпрямитель не пропускает тона и напряжение на нагрузке равно нулю. Таким образом, напряжение на нагрузке имеет форму полусинусоид.
Мостовая схема
(выпрямители работают попарно)
В первый полупериод, когда ЭДС действует согласно положительным направлениям напряжение на выпрямителях 1 и 3 , эти выпрямители проводят ток, а выпрямители 2 и 4 тока не проводят и наоборот.
ωt
Аппроксимация характеристик нелинейных элементов
Как правило, ВАХ нелинейных элементов получают экспериментально; реже удается найти их из теоретического анализа. Для исследования необходимо подобрать функцию аппроксимации такую, которая, будучи довольно простой, отражала бы все возможные особенности экспериментальной снятой характеристики с достаточной степенью точности. Чаще всего используют следующие способы аппроксимации вольт-амперных характеристик двухполюсников: кусочно-линейная, степенная, показательная аппроксимация.
Кусочно-линейная аппроксимация
Такую аппроксимацию обычно применяют при рассчете процессов в нелинейных уравнениях в случае больших амплитуд внешних воздействий. Данный способ основан на апроксимации характеристик нелинейных элементов, т.е. на приближенной замене реальной характеристики отрезками прямых линий с различными наклонами. На рисунке показана входная характеристика реального транзистора, аппроксимированная двумя отрезками прямых.
![]()

![]()
Аппроксимация определяется двумя параметрами – напряжением начала характеристики Uн и крутизной S. Математическая форма аппроксимированной ВАХ такова:
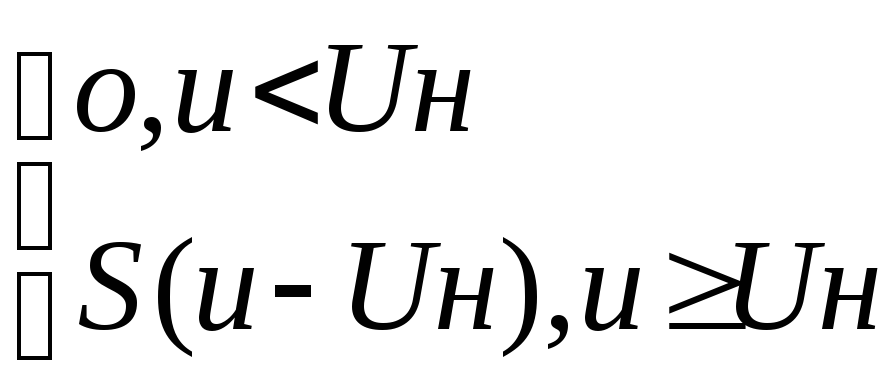
Напряжение начала входных характеристик биполярных транзисторов имеет порядок 0,2-0,8 В: крутизна характеристики тока базы iб(Uбэ) около 10мА/В. Крутизна характеристики iк(Uбэ) тока коллектора в зависимости от напряжения база-эмиттер, то величина 10мА/В должна быть умножена на h21э – коэффициент усиления тока базы. Поскольку h21э = 100-200, указанная крутизна имеет порядок нескольких ампер на вольт.
Степенная аппроксимация
Степенную аппроксимацию широко используют при анализе работы нелинейных устройств, на которые подаются относительно малые внешние воздействия. Этот способ основан на разложении нелинейной вольт-амперной характеристики i(u) в ряд Тейлора, сходящийся в окрестности рабочей точки U0.
i(u)
=
![]()
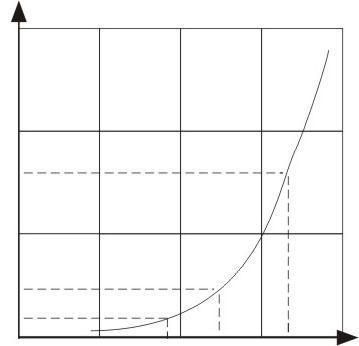
количество членов разложения зависит от заданной точности. Рассмотрим пример:
![]()
0,5
0,7 0,9
![]()
Входная характеристика транзистора. Рабочая точка U0=0,7В. Выбираем в качестве узлов аппроксимации точки 0,5; 0,7 и 0,9 В.
Необходимо решить систему уравнений :
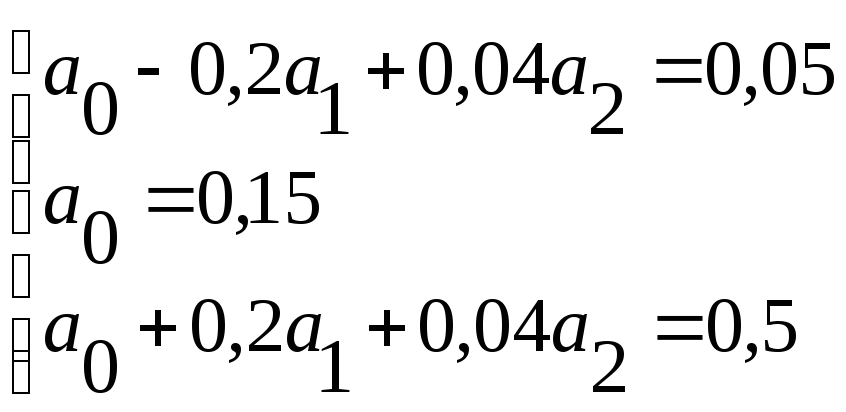
Спектральный состав тока в нелинейном элементе при внешнем гармоническом воздействии
Рассмотрим
цепь, состоящую из последовательного
соединения источника гармонического
сигнала Uс(t)
=
![]() cost,
источника постоянного напряжения
смещения U0
и безинерционного нелинейного
элемента. Для этого рассмотрим рисунок.
cost,
источника постоянного напряжения
смещения U0
и безинерционного нелинейного
элемента. Для этого рассмотрим рисунок.
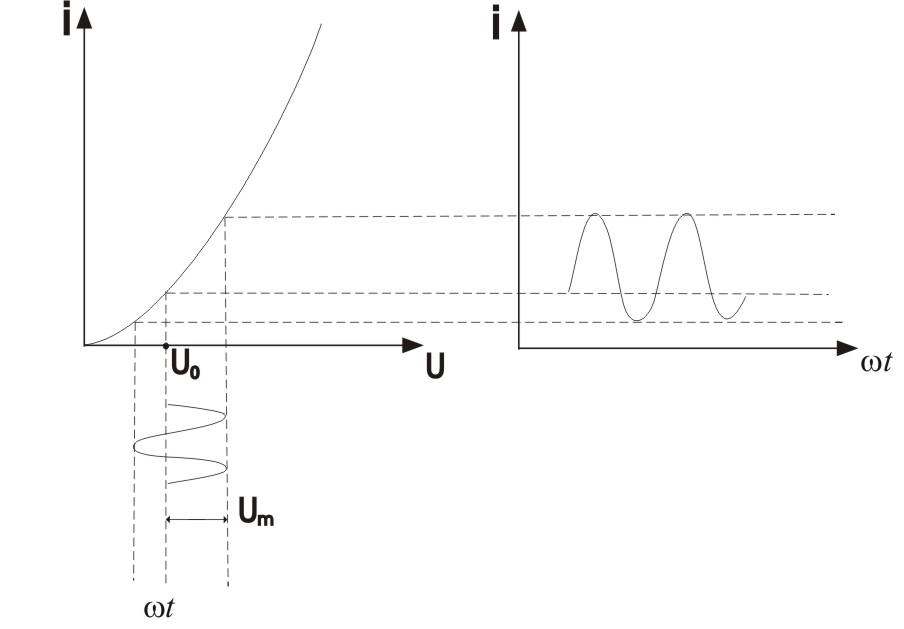
Ток в цепи имеет синусоидальную форму.
Форма тока и напряжения оказываются различными.
Причина
искажения кривой тока проста: одинаковым
приращениям напряжения отвечают
неодинаковые приращения тока, т.к.
![]() , а дифференциальная крутизна ВАХ на
разных участках различна.
, а дифференциальная крутизна ВАХ на
разных участках различна.
Рассмотрим задачу аналитически.
Пусть нам известна нелинейная функция i(u)=i(Uc,U0). На нелинейный элемент действует напряжение сигнала Uc(t)=Umcos(t+).
Безразмерная величина
=t+,
тогда I()=I(Umcos,
U0)
– переодическая функция относительно
аргумента с периодом
2T. Представим ее рядом Фурье
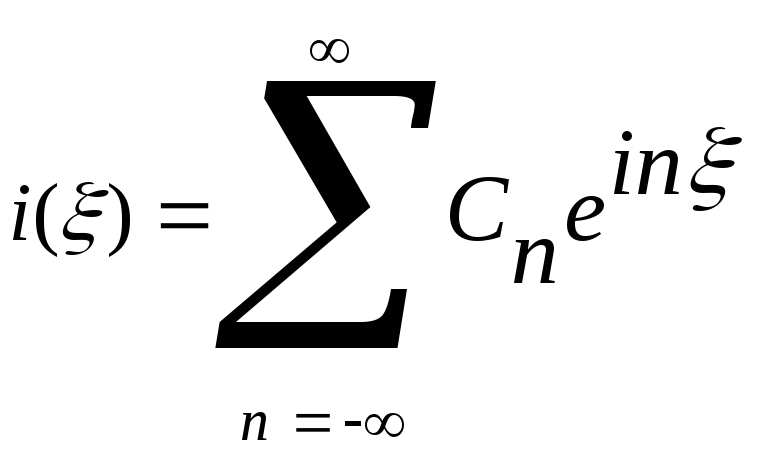 с коэффициентами
с коэффициентами
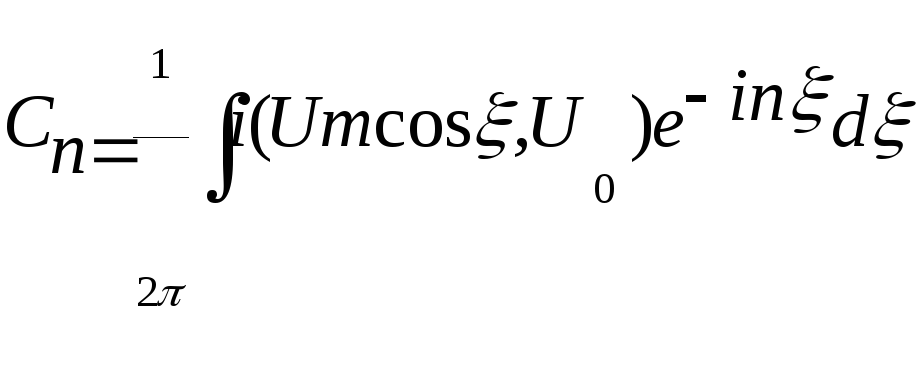 .
.
Функция
i()
четная, поэтому ряд Фурье будет содержать
только косинусные составляющие:
 .
.
Амплитудные коэффициенты гармонии
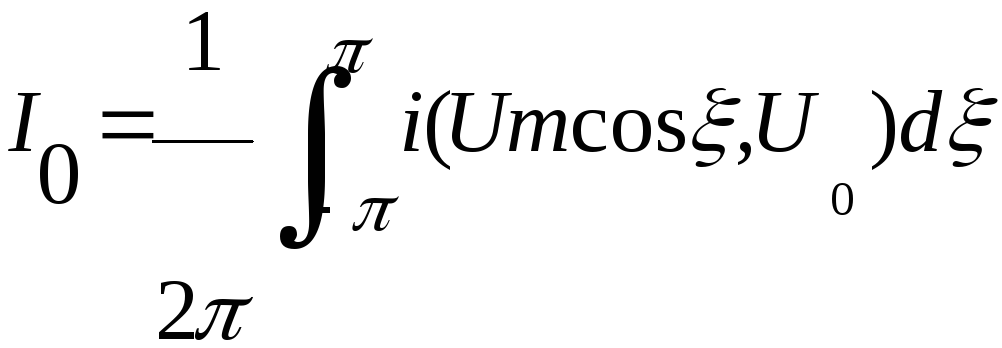
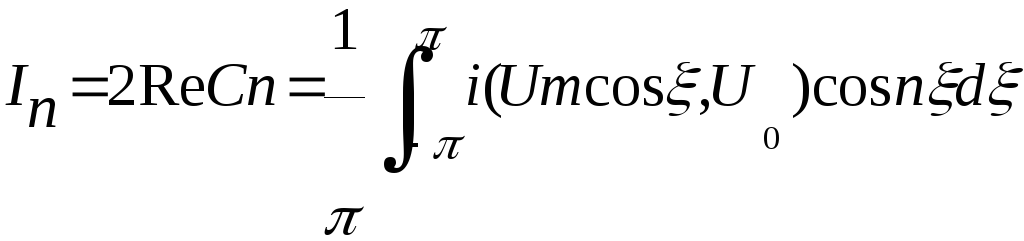
n=1,2,…
Две последние формулы дают общее решение задачи о спектре тока в нелинейном элементе при гармоническом внешнем воздействии:
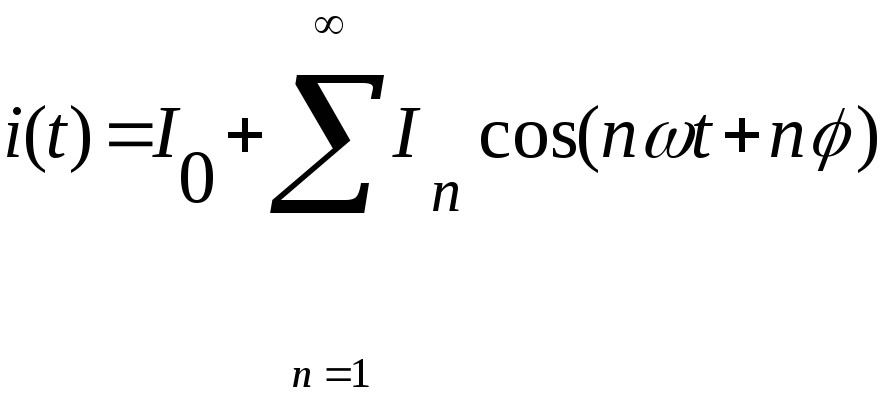
т.е. ток, кроме постоянной составляющей I0, содержит бесконечную последовательность гармонии с амплитудами In. Амплитуды гармонии зависят от параметров Um и U0, а также от вида аппроксимирующей функции.
Рассмотрим каким образом зависит от вида аппроксимирующей функции.
Кусочно-линейная

i(U)=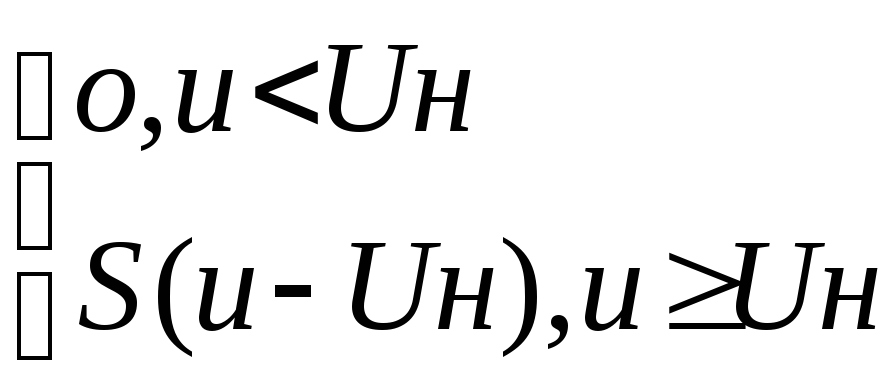
Подано напряжение u(t)=U0+Umcost.
График тока имеет вид косинусоидальных импульсов с отсечкой. Угол отсечки импульсов тока определяется из равенства:
U0+Umcos=Uн
![]() .
.
Степенная аппроксимация.
Пусть в окрестности рабочей точки U0 ВАХ нелинейного элемента представлена в виде:
i(u)
=
![]() +…
+…
На вход подается напряжение:
u(t)=Uo+Umcosωt
Подставляя получаем:
![]()
![]()
![]()
![]()
![]()
![]()
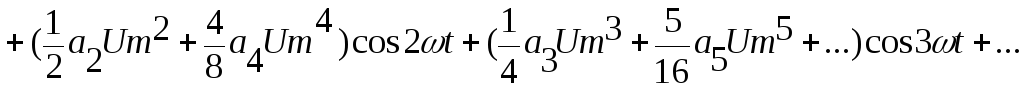
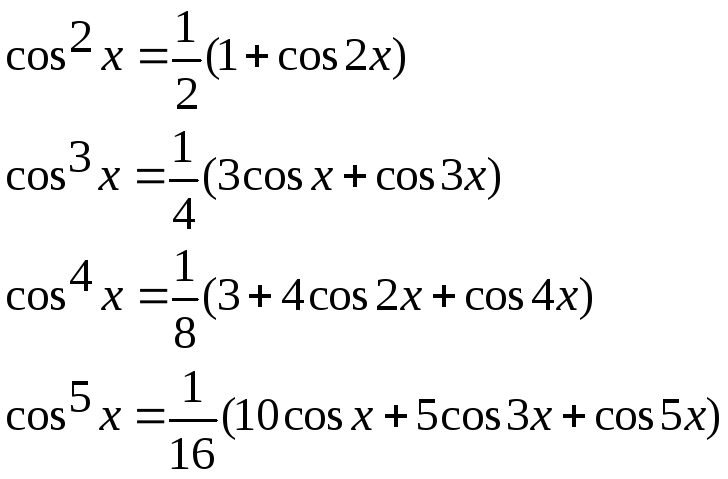
Получаем соотношения для расчета постоянной составляющей и амплитуд гармоник тока.
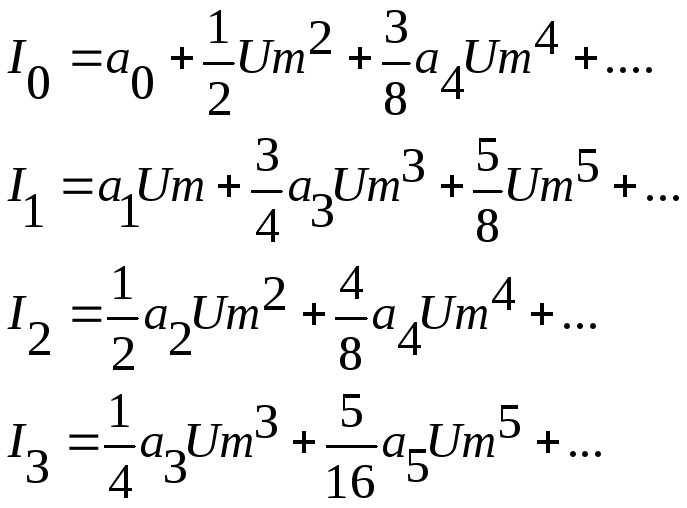
Постоянная составляющая и амплитуды четных гармоник определяются коэффициентами степенного ряда с четными номерами. Амплитуды нечетных гармоник зависят лишь от нечетных номеров.
Общее выражение:
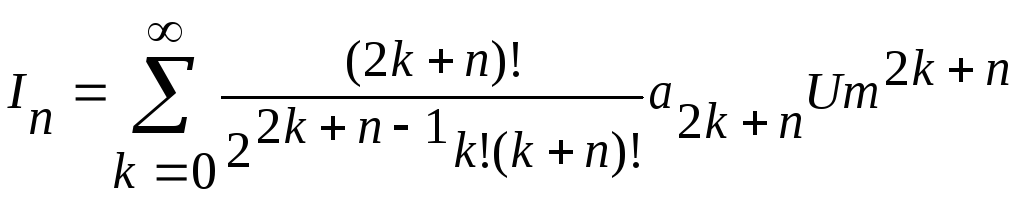
Нелинейные искажения в усилителе с резистивной нагрузкой
Преобразование спектра входного сигнала в нелинейных цепях является важным явлением. С одной стороны, на нем основана работа целого ряда радиотехнических устройств (модуляторов, детекторов); с другой, из-за нелинейности характеристик возникают нежелательные эффекты.
Рассмотрим транзисторный усилитель, нагрузкой которого служит резистор Rн
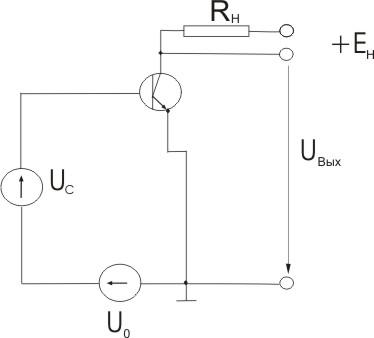
Будем полагать, что амплитуда входного сигнала Umвх достаточно велика для того, чтобы учитывать нелинейность характеристики транзистора iк (Uбэ). Пусть эта характеристика задается многочленом второй степени:
![]()
На входе Uбэ=U0+Umвхcosωt.
В коллекторной цепи будем иметь постоянную составляющую тока, а также токи, отвечающие первой и второй гармоникам частоты сигнала.
![]() Umвх
,
Umвх
,
![]()
Эти гармоники тока, проходя через резистор нагрузки, создают на нем падение напряжения, которое является входным сигналом. Для того, чтобы количественно оценить степень искажения сигнала на выходе усилителя, вводят величину kн – коэффициент нелинейных искажений.
Эта величина равна отношению среднеквадратического уровня всех внешних гармоник тока и амплитуде тока полезного сигнала:
![]()
В данном случае :
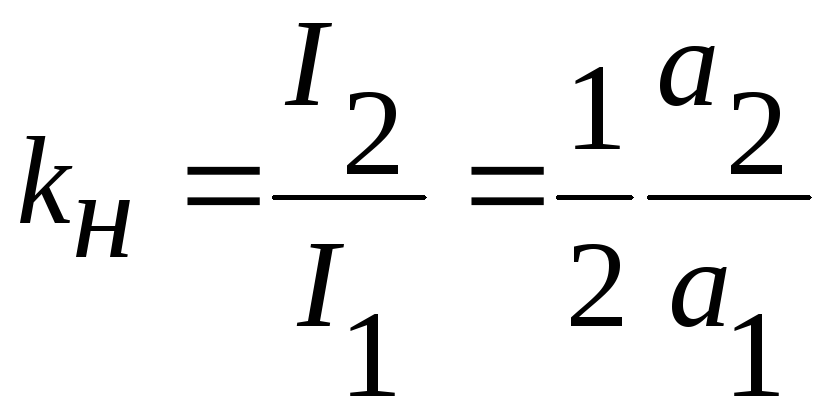 Umвх.
Umвх.
Т.к.
![]() увеличивается с ростом нелинейных
искажений
увеличивается с ростом нелинейных
искажений
Нелинейные резонансные усилители
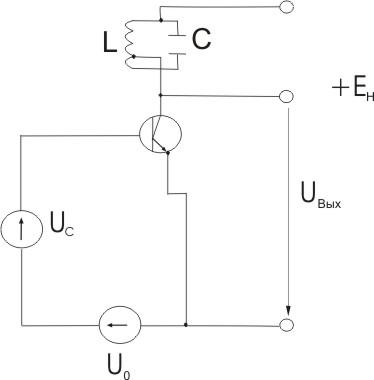
Рассмотрим транзисторный усилитель с нагрузкой в виде параллельного колебательного контура.
На вход усилителя подано напряжение: Uвх(t)=U0+Umвхcost.
Колебательный контур настроен на частоту: рез=. Предположим, что характеристика iк (Uбэ) транзистора аппроксимирована отрезками прямых. Тогда, ток в цепи коллектора имеет форму косинусоидальных импульсов с отсечкой. Эти импульсы обладают сложным спектральным составом. Однако основную роль в работе устройства играет лишь первая гармоника тока, частота которой совпадает с резонансной частотой контура. Высшие гармоники практически не дают вклада в выходной сигнал
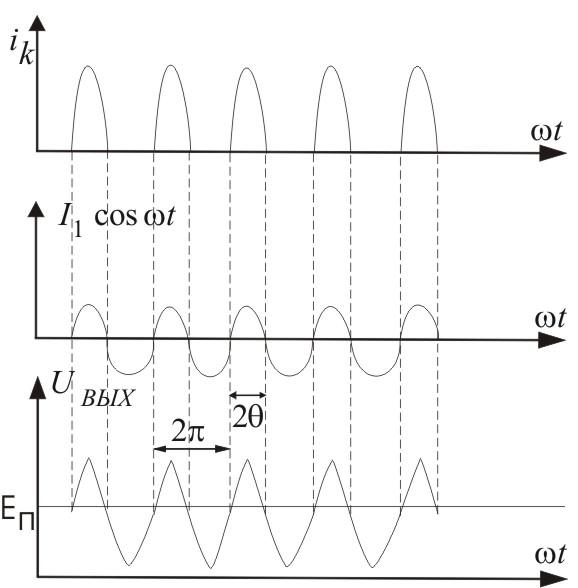
Первая гармоника
коллекторного тока создает на выходе
полезное напряжение с амплитудой:Umвх
= Ii Rрез =
SRрезUmвх1(![]() ).
).
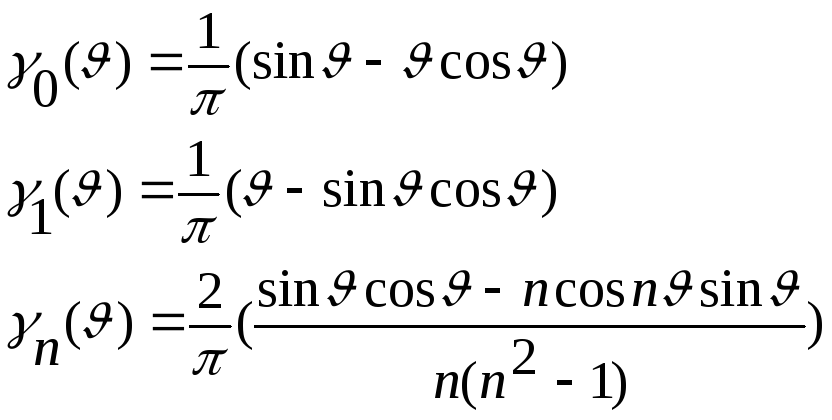 при
n=2,3…
при
n=2,3…
, где
![]() - коэффициент Берга.
- коэффициент Берга.
При степенной аппроксимации
Umвых![]() Umвх
+
Umвх
+
![]() Umвх
Umвх![]() +
+
![]() Umвх
Umвх![]() +…)
+…)
Зависимость Umвых = f(Umвх) называется колебательной характеристикой. Колебательная характеристика в общем случае нелинейна, т.к. угол отсечки , а значит, и коэффициент Берга зависят от амплитуды возбуждающего напряжения Umвх. Исключение составляет случай, когда положение рабочей точки совпадает с началом характеристики. При этом угол отсечения равен 90ْْ независимо от Umвх. Работа усилителя с углом отсечения 90ْ выгодна еще и потому, что в отсутствии высокочастотного сигнала (режим “молчания”) постоянная составляющая коллекторного тока обращается в нуль. Данное обстоятельство благопрятно сказывается на КПД усилителя.
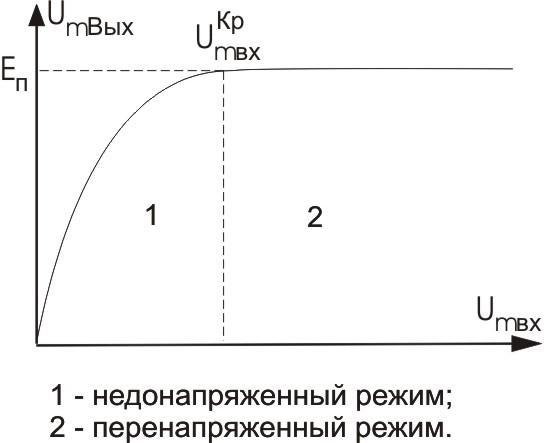
Важным параметром колебательной характеристики является ширина ее линейного участка, который определяет динамический диапазон усиливаемых сигналов. Естественная причина, которая ограничивает рост колебательной характеристики, состоит в следующем: при некотором критическом значении амплитуды входного сигнала Umвх кр колебательное напряжение на контуре становится близким по значению и напряжению источника питания Eпит. Дальнейший рост амплитуды напряжения на контуре становится невозможным.
При этом в некоторые моменты времени мгновенное значение напряжения на коллекторе транзистора становится малым. Как следствие, нормально запертый коллекторный переход открывается и цепь: “коллектор – база - источник сигнала - источник питания” резко шунтирует (замыкает) колебательную систему усилителя.
Если Umвх
> Umвх![]() , то говорят,
что усилитель работает в перенапряженном
режиме.
, то говорят,
что усилитель работает в перенапряженном
режиме.
Одной
из важных характеристик является КПД.
Чтобы вычислить КПД, необходимо знать
мощность, потребляемую от источника
питания: Pпит=En
I0
и полезную активную мощность, передаваемую
колебателному контуру :
![]() .
.
В мощных усилителях обычно стремятся максимально полно использовать источник питания, приближаясь к границе перенапряженного режима, т.е.: Umвх Епит.
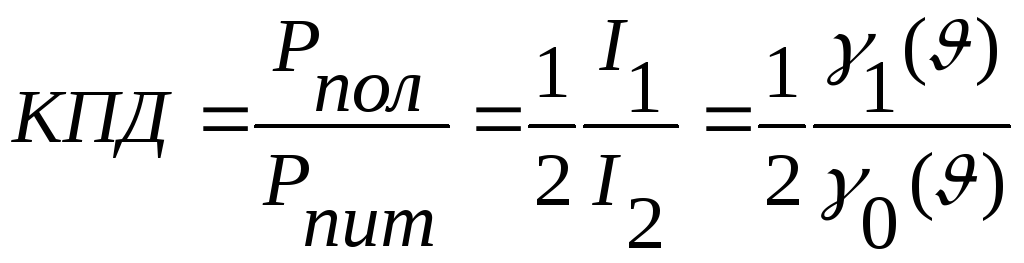 (*)
(*)
Т.е. определяется отношением (*). Это отношение максимально и равно 2 при =90ْ (КПД=1/2x2=1). С ростом это отношение уменьшается (при =90ْ равно 1,57. КПД=1/2x0,78). Поэтому с точки зрения эффективности использования источника питания выгоден режим с малым углом отсечки, когда КПД усилителя приближается к единице. Однако при этом резко снижается коэффициент 1 и для получения заданной полезной мощности приходится увеличивать амплитуду входного сигнала, что не всегда возможно. Принимая во внимание требование линейности колебательной характеристики, на практике идут на некоторое снижение КПД и выбирают угол отсечки, близкий к 90ْ.
Резонансное умножение частоты
Если в схеме резонансного усилителя, работающего с большой амплитудой входного сигнала, колебательная система будет настроена на частоту n - частоту одной из высших гармоник входного сигнала, то данное устройство может использоваться в качестве умножителя частоты.
Когда возникает необходимость в умножителях? Если необходимо создать источник гармонических колебаний с высокой стабильностью частоты, а непосредственное генерирование колебаний в заданном диапазоне невозможно, но имеется в распоряжении стабильный низкочастотный генератор.
Расчеты умножителей частоты и нелинейных резонансных усилителей в принципе не отличаются. Амплитуда выходного сигнала умножителя при кусочно-линейной аппроксимации:
Umвых
=
![]() Umвхn(
Umвхn(![]() ).
).
Но есть
трудности при создании умножителей
частоты. n(![]() )
при большой кратности (n)
имеет низкое значение. Поэтому следует
выбирать углы отсечки, максимизирующие
соответствующие коэффициенты Берга.
)
при большой кратности (n)
имеет низкое значение. Поэтому следует
выбирать углы отсечки, максимизирующие
соответствующие коэффициенты Берга.
Чем выше скваженность последовательности импульсов коллекторного тока, тем богаче их спектральный состав. Отсюда следует, что, желая создать умножитель с высокой кратностью, следует выбирать малые углы отсечки. При этом оптимальным считается:
опт=120ْ/n
Именно таким должен быть угол отсечки тока в умножителе частоты.
Свойство нелинейной цепи обогащать спектр, создавая на выходе спектральные составляющие, первоначально отсутствующие на входе, лучше всего проявляется, если входной сигнал представляет собой сумму нескольких колебаний с различными частотами.
Нелинейные преобразования суммы нескольких гармонических сигналов
Будем изучать нелинейный двухполюсник, ВАХ которого описывается многочленом второй степени :
i(u)
=
![]()
Приложенное напряжение помимо постоянной составляющей содержит два гармонически колбанияс различными частотами 12; амплитуды колебаний равны Um1 и Um2.
![]()
Такой сигнал называется бигармоническим.
Получаем:
![]()
Выполним тригонометрические преобразования:
![]()
![]() .
.
В составе тока присутствуют слагаемые, встречавшиеся ранее: постоянная составляющая, а также первые и вторые гармоники обоих источников входного сигнала. Новым является появление двух гармонических составляющих с частотами (1+2) и (1-2). Амплитуды этих колебаний a2Um1Um2 зависят от амплитуд входных сигналов и обращаются в нуль, если один из источников на входе отсутствует. Т.е. из-за нелинейности рассматриваемого двухполюсника в нем происходит взаимодействие двух колебаний, соответствующих отдельным гармоническим составляющим входного сигнала.
Переходные процессы в линейных электрических цепях.
Под переходными процессами понимают процессы перехода от одного режима работы электрической цепи к другому, чем-либо отличающемуся от предыдущего, например величиной амплитуды, фазы, формой или частотой. Переходные процессы вызываются коммутацией в цепи. Коммутация - это процесс замыкания или размыкания выключателей. Переходные процессы обычно являются быстро протекающими. Изучение переходных процессов важно, т.к. оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, выяснить всевозможные увеличения амплитуд токов, которые могут в десятки раз превышать амплитуду тока установившегося процесса.
Запишем уравнение по второму закону Кирхгофа при замкнутом
р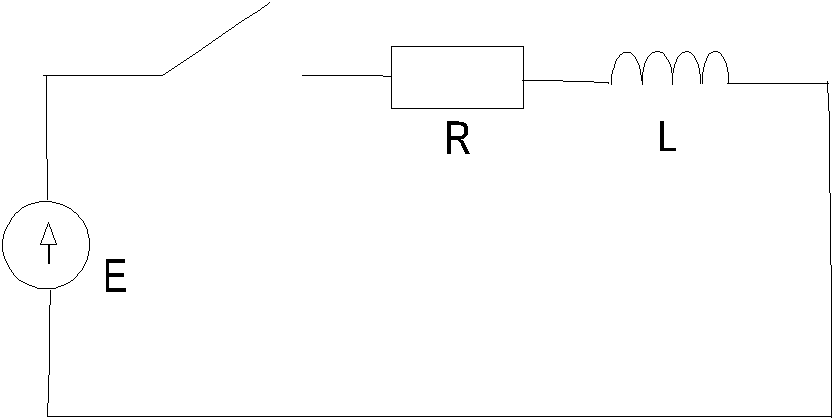 убильнике.
убильнике.
![]() Сумма падений
напряжения на L
и R
= эдc
E
Сумма падений
напряжения на L
и R
= эдc
E
![]()
![]() или
или
Общий интеграл линейного дифференциального уравнения равен сумме частного решения неоднородного уравнения + общее решение однородного уравнения . Частное решение для уравнения (1) = E/R
![]()
![]() Однородное
решение получаем из исходного, если в
нем взять правую часть = 0. Решением
однородного уравнения является
показательная фунция : Aept.
Для всех переходных процессов условимся,
что момент t=0
соотвествует моменту коммутации.
Однородное
решение получаем из исходного, если в
нем взять правую часть = 0. Решением
однородного уравнения является
показательная фунция : Aept.
Для всех переходных процессов условимся,
что момент t=0
соотвествует моменту коммутации.
![]() Решение
уравнения (1)
Решение
уравнения (1)
Подставим в (1) и получим тождество
![]()
![]() Частное решение
неоднородного дифференциального
уравнения будем называть принужденной
составляющей тока , а полное решение
уравнения - свободной
составляющей . Полная величина тока
Частное решение
неоднородного дифференциального
уравнения будем называть принужденной
составляющей тока , а полное решение
уравнения - свободной
составляющей . Полная величина тока
Принужденная составляющая тока физически представляет собой составляющую, изменяющуюся с той же частотой , что и действующая в схеме принуждающая э.д.с. Так, если в схеме действует принуждающая синусоидальная э.д.с. частоты w , то принужденная составляющая любого тока в схеме является соотвественно синусоидальным током частоты w . Если в схеме действует постоянный э.д.с., то принужденный ток есть постоянный ток.
В линейных электрических цепях свободные составляющие токов и напряжений затухают во времени по показательному закону ept
Из трех токов (полного, принужденного и свободного) основое значение имеет полный ток. Полный ток является тем током , который в действительности протекает по той или иной ветви цепи при переходном процессе. Его можно измерить и записать на осциллограмме .
1 закон коммутации.
![]()
![]() Ток через
индуктивность непосредственно до
коммутации iL(0_)
равен току через ту же индуктивность
непосредственно после коммутации iL(0+)
Ток через
индуктивность непосредственно до
коммутации iL(0_)
равен току через ту же индуктивность
непосредственно после коммутации iL(0+)
2 закон коммутации.
![]()
![]() Напpяжение
на емкости непосредственно до коммутации
UC(0_)
равно напряжению - после коммутации
UC(0+)
Напpяжение
на емкости непосредственно до коммутации
UC(0_)
равно напряжению - после коммутации
UC(0+)
Д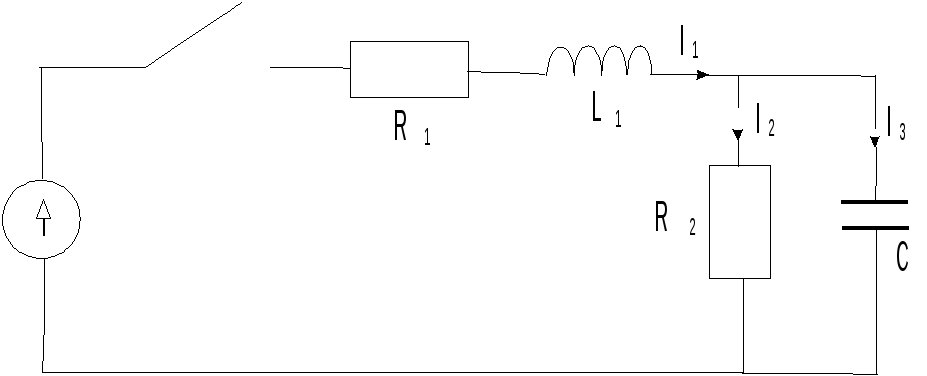 ля
послекоммутационной схемы составляют
уравнение по законам Кирхгофа для полных
токов.
ля
послекоммутационной схемы составляют
уравнение по законам Кирхгофа для полных
токов.
![]()
![]()
![]()
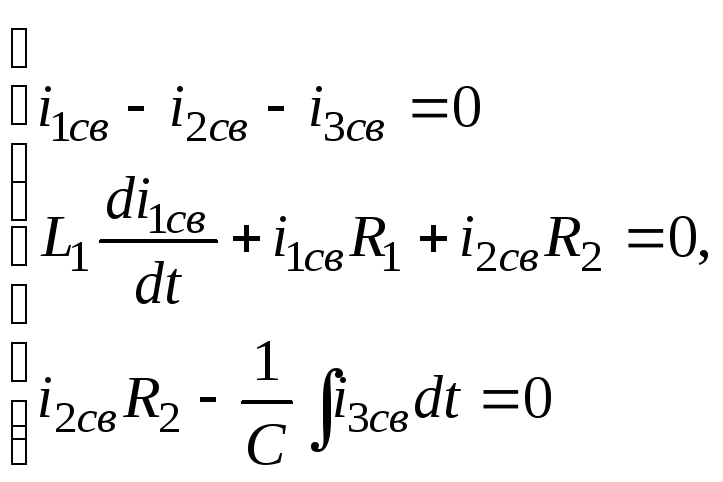
![]() В этих уравнениях
i1,
i2,
i3
- полные токи. Для того чтобы от этой
системы уравнений перейти к уравнениям
для свободных токов, освободим систему
от вынуждающих э.д.с. и вместо i1
запишем
i1св
, и т.д.
В этих уравнениях
i1,
i2,
i3
- полные токи. Для того чтобы от этой
системы уравнений перейти к уравнениям
для свободных токов, освободим систему
от вынуждающих э.д.с. и вместо i1
запишем
i1св
, и т.д.
![]()
![]()
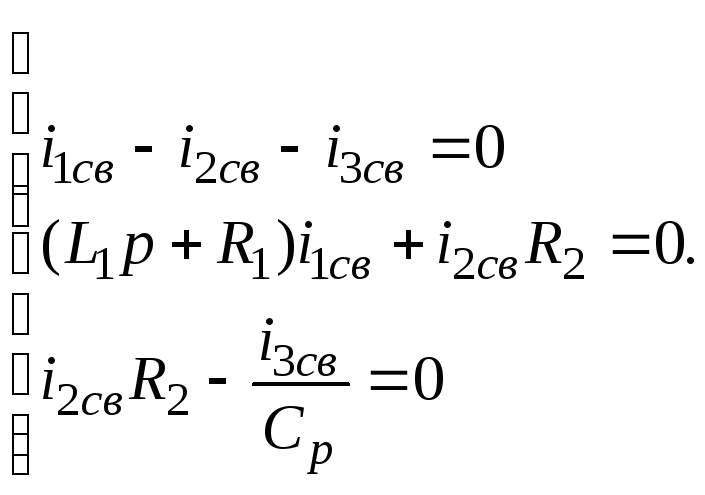
![]()
![]()
Это уравнение представляет собой систему алгебраических уравнений и не
содержит производных и интегралов.
Переход от систему дифференциальных уравнений к системе алгебраических уравнений из алгебраизацией системы дифференциальных уравнений.
![]()
![]()
![]()
-
-
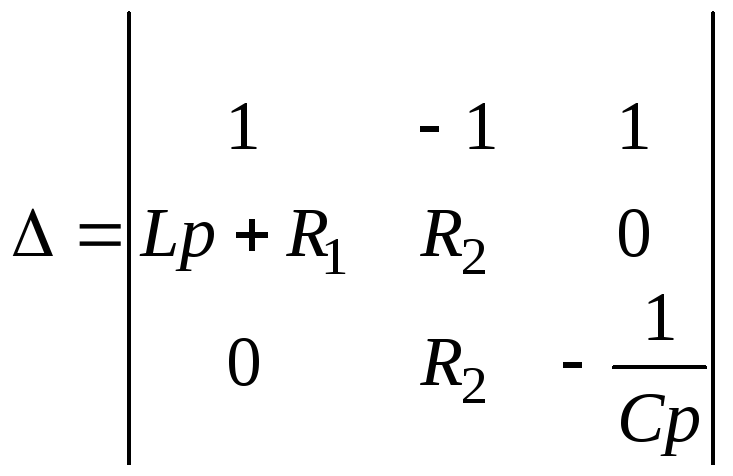 определитель системы.
определитель системы.
1 получают из определителя системы путем замены первого столбца правой частью уравнения 5.
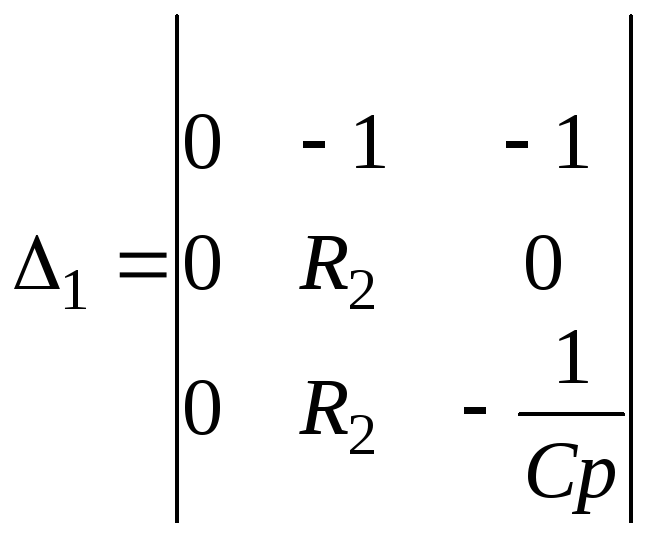
2 получают из путем замены второго столбца правой частью системы (5). Если в определителе один из столбцов состоит из нулей, то 1=0, 2 =0, 3=0.
![]()
![]()
![]() Свободные токи
могут быть не равны нулю в том случае,
если определитель системы =0.
Уравнение =0
из характеристическим уравнением.
Свободные токи
могут быть не равны нулю в том случае,
если определитель системы =0.
Уравнение =0
из характеристическим уравнением.
![]()
![]()
![]()
![]()
![]()
![]() Если дробь
равна 0, то равен 0 ее числитель. =>
Если дробь
равна 0, то равен 0 ее числитель. =>
Говорилось, что iсв=Aept.
Если характеристическое уравнение будет иметь не один корень, а несколько, например n, то для каждого свободного тока нужно взять
![]()
Характеристическое уравнение для определения p часто составляют более простым путем. С этой целью составляют выражение входного сопротивления для любой ветви цепи на переменном токе z(jw), заменяют в нем jw на p и приравнивают z(p) и нулю.
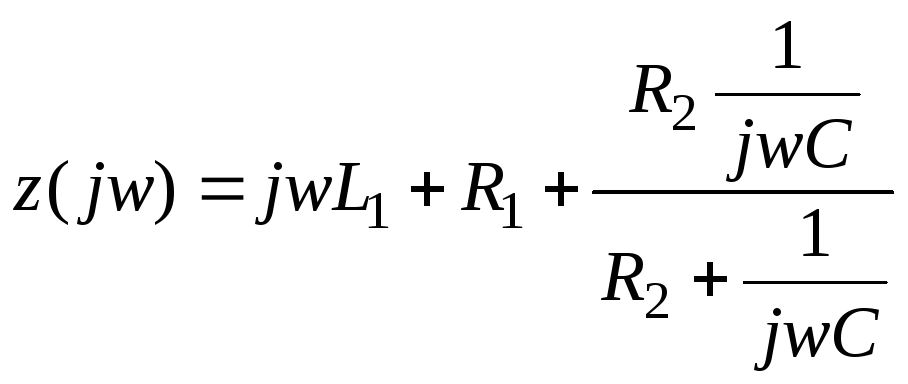 Для схемы на
рис.
Для схемы на
рис.
Jw=p и равен 0
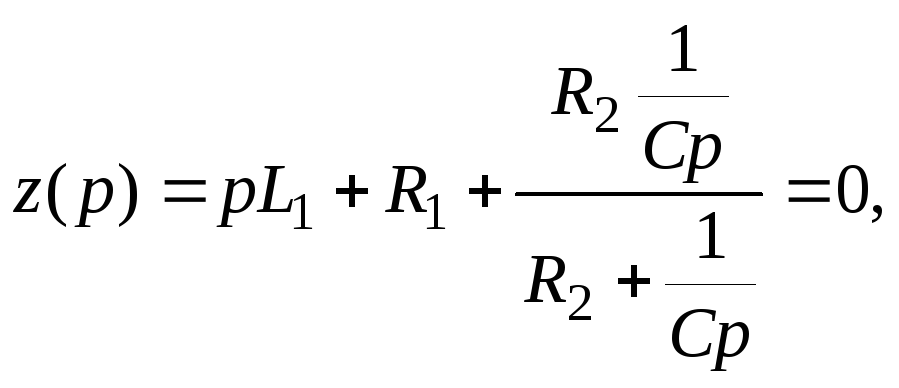
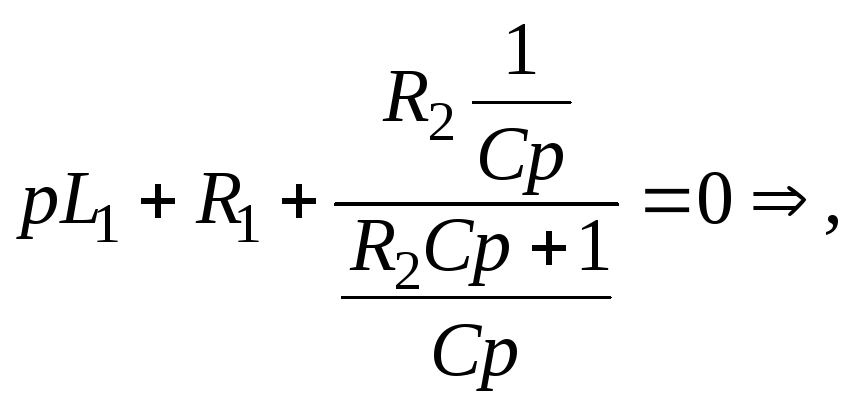
![]()
![]() Уравнения
полностью совпадают.
Уравнения
полностью совпадают.
Число корней характеристического уравнения = степени этого уравнения.
Уравнение 1 степени имеет всегда отрицательный действительный корень.
Уравнение 2 степени может иметь:
а) 2 действит. неравных отрицат. корня;
б) 2 действит. равных отрицат. корня;
в) 2 комплексно сопр. корня с отрицат. действит. частью.
Уравнение 3 степени может иметь:
а) 3 действит. неравных отрицат. корня;
б) 3 действит. отрицат. корня, из которых 2 равны друг другу;
в) 3 действит. равных отрицат. корня;
г) 1 действит. отрицат. корень и 2 сопряж. с отрицат. действит. частью.
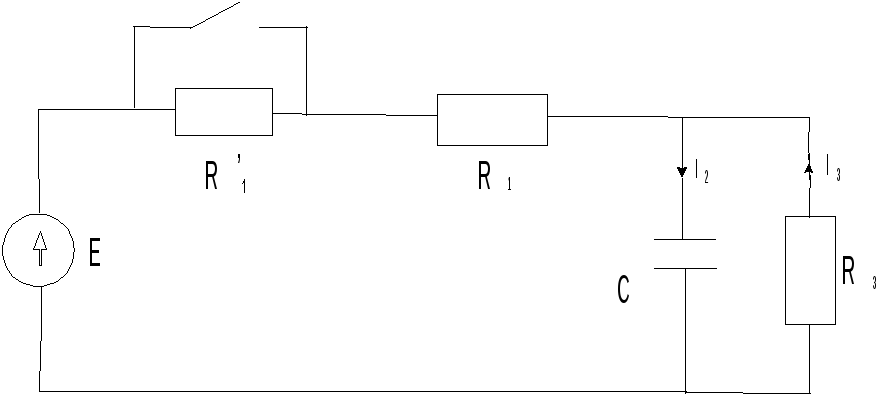 R1=R'1=R3=50
Ом, С=100 мкф, Е=150 В.
R1=R'1=R3=50
Ом, С=100 мкф, Е=150 В.
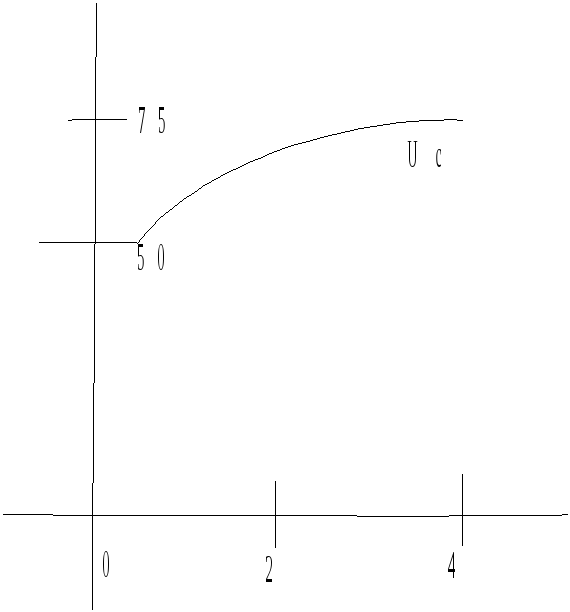
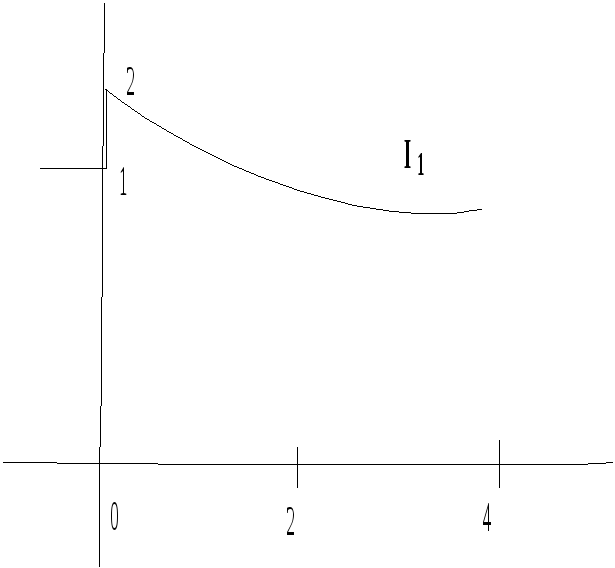
Требуется: 1) найти полные, принужденные и свободные составляющие токов и напряжения на конденсаторе j, 2) определить токи i1, i2,i3 и напряжение Uc в фунции времени.
![]()
![]() До коммутации
До коммутации
![]() Напряжение на
конденсаторе равнялось напряжению на
сопротивлении R3
Напряжение на
конденсаторе равнялось напряжению на
сопротивлении R3
Принужденные значения после коммутации:
![]()
![]()
![]()
![]() По второму
закону Кирхгофа составим уравнение для
контура, образованного первой и второй
ветвями при t=0+
По второму
закону Кирхгофа составим уравнение для
контура, образованного первой и второй
ветвями при t=0+
![]()
![]() Из уравнения
Из уравнения
![]()
По первому закону Кирхгофа
![]()
![]()
Свободные составляющие найдем как разности между полными и принужденными составляющими.
![]()
![]()
![]()
![]()
Характеристическое уравнение схемы
![]()
![]()
![]()
![]()
![]()
![]() имеет
один корень
имеет
один корень

Преобразование Лапласа.
Переход от фунции времени и фунции p осуществляется с помощью преобразования Лапласа. Операторный метод расчета позвооляет свести операцию дифференцирования к умножения, а операцию интегрирования - к делению.
Условимся под понимать комплексное число p=a+jb
![]()
![]()
![]()
 Фунцию времени
обозначают f(t)
и называют оригиналом. Ей соотвествует
фунция F(p),
называемая изображением.
Фунцию времени
обозначают f(t)
и называют оригиналом. Ей соотвествует
фунция F(p),
называемая изображением.
![]()
![]()
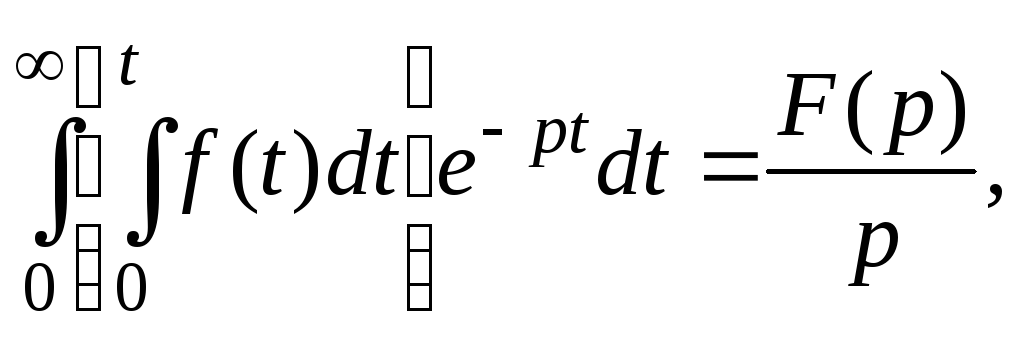

Выразим потенциал точки A через потенциал точки B.
![]()
![]()
Вместо , вместо
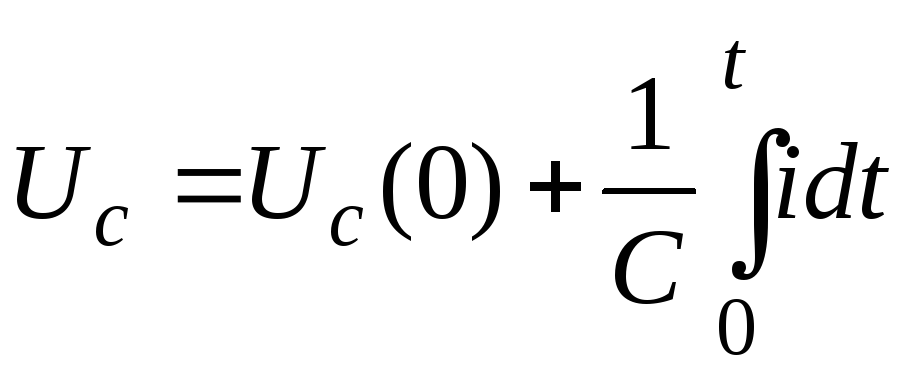
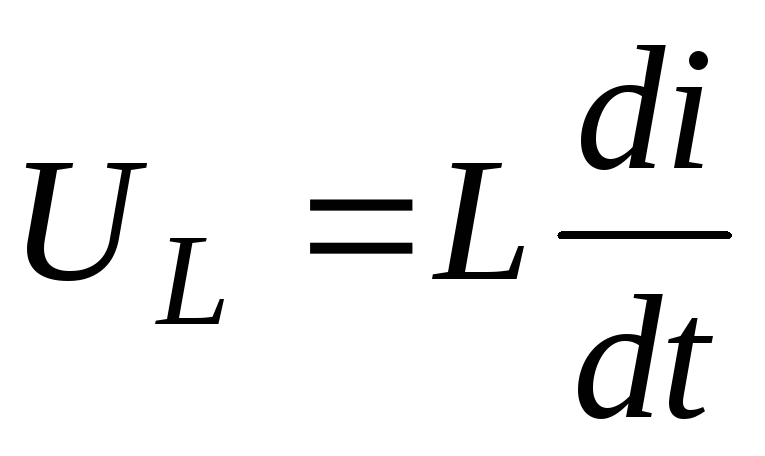
![]()
![]()
![]()
![]()
![]() Применим
преобразование Лапласа.
Применим
преобразование Лапласа.
![]()
![]()
![]()
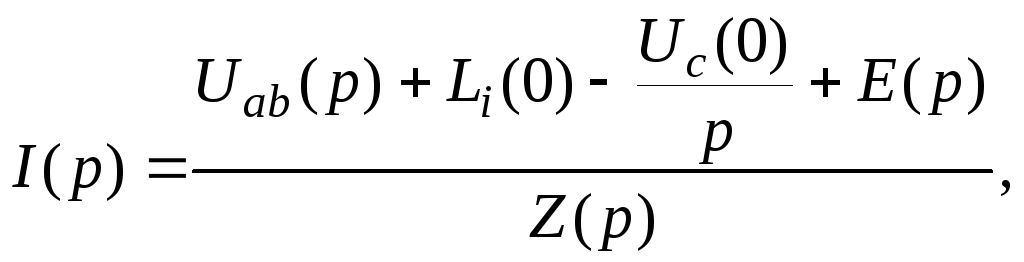
![]() где
где
Z(p) представляет собой операторное сопротивление участка цепи. Это уравнение из закона Ома в операторной форме для участка цепи, содержащего э. д. с.
![]() В частном
случае, когда на участке ab
отсутствует э. д. с. и к моменту коммутации
i(0)=0
и Uc(0)=0
В частном
случае, когда на участке ab
отсутствует э. д. с. и к моменту коммутации
i(0)=0
и Uc(0)=0
![]()
![]() Первый закон
Кирхгофа в операторной форме
Первый закон
Кирхгофа в операторной форме
![]()
![]() Второй закон
Кирхгофа в операторной форме
Второй закон
Кирхгофа в операторной форме
Четырехполосник и его основные уравнения.
Ч![]()
![]() етырехполосником
называют электрическую схему, имеющую
два входных и два выходных зажима.
Принято изображать четырехполосник в
виде прямоугольника
етырехполосником
называют электрическую схему, имеющую
два входных и два выходных зажима.
Принято изображать четырехполосник в
виде прямоугольника

![]()
Входной
ток
![]()
Входное
напряжение
![]()
Ток и
напряжение на выходе
![]() и
и![]()
К зажимам mn - источник питания
pq – нагрузка.
Для
любого пассивного Линейного четырехполосника
напряжение и ток на входе
![]() и
и
![]() связаны с напряжением и током на выходе
связаны с напряжением и током на выходе
![]() и
и
![]() двумя основными уровнениями:
двумя основными уровнениями:
![]() (1) ;
(1) ;
![]() (2) ; коофициенты связаны соотношением:
(2) ; коофициенты связаны соотношением:
![]() (3).
(3).

Напряжение на нагрузке
![]()
Заменим
нагрузку
![]() на э.д.с.
на э.д.с.
![]() , направленную встречно току
, направленную встречно току
![]() и
и
численно
равную
![]() .
.
Запишем
выражения для токов
![]() и
и
![]() через
через
![]() и
и
![]() и
входные и заимные
проводимости
ветвей. Если токи
и
входные и заимные
проводимости
ветвей. Если токи
![]() и
и
![]() рассматривать как контурные токи, то
рассматривать как контурные токи, то
э.д.с. контуров ,совпадающие с направлением контурных токов, войдут в уравнение со знаком «+», а э.д.с. не совпадающие с направлением соответствующих контурных токов, войдут со знаком «-».
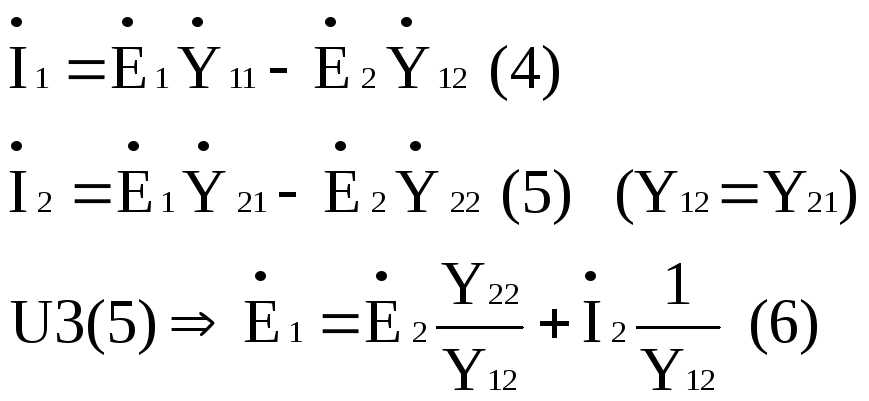
Подставим (6) в (4)
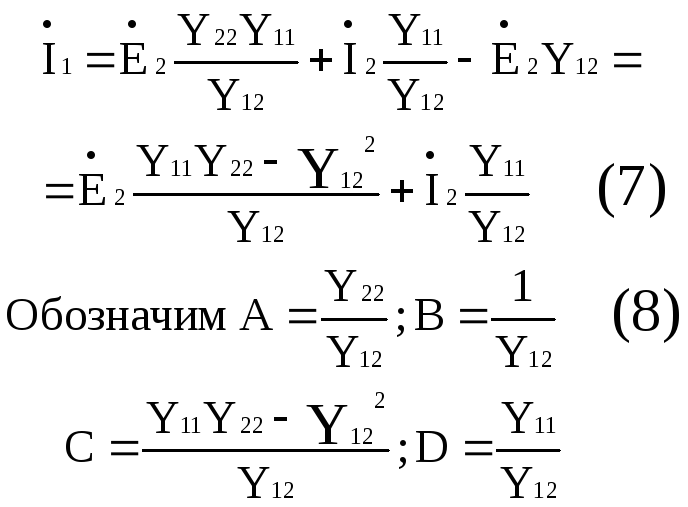
Заменив
в (6) и (7)
![]() на
на
![]() и
и
![]() на
на
![]() и
воспользовавшись обозначениями (8),
получим основные уравнения четырехполосника
и
воспользовавшись обозначениями (8),
получим основные уравнения четырехполосника
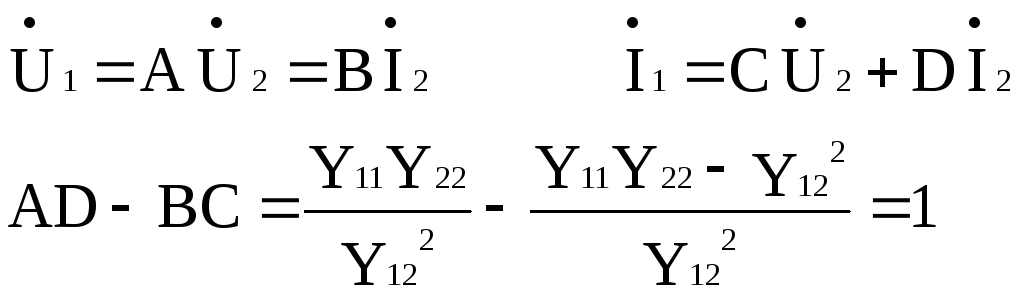
Проверим
какая связь существует между напряжением
и токами, если источник
![]() присоединить
к зажимам pq
, а нагрузку - к зажимам mn
присоединить
к зажимам pq
, а нагрузку - к зажимам mn
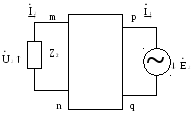
Как и
в предыдущем выводе, замена![]()
на
э.д.с.
![]()

Заменим
![]() на
на
![]() и
и![]() на
на
![]() и воспользовавшись (8), перепишем (11) и
(12)
и воспользовавшись (8), перепишем (11) и
(12)
![]()
Четрехполосник называется симметричным, если при перемене местами источника питания и нагрузки, токи в источнике питания и в нагрузке не изменяются (A = D).
Систему уравнений (1) и (2) называют A-формой записи уравнений четырехполосника.
![]()
Для
A-формы
положительные направления токов
![]() и
и
![]() соответствуют
изображенным на рис. 1.
соответствуют
изображенным на рис. 1.
Кроме A-формы, могут быть записаны еще 5 форм уравнений четырехполосника Y, Z, H, G ,B.
Для
Y,
Z,
H
и G-форм
записи положительное направление тока
![]() такое
же как на рис.1, а направление тока
такое
же как на рис.1, а направление тока
![]() противоположно
изображенному на этом рисунке. Для
B-формы
направления
противоположно
изображенному на этом рисунке. Для
B-формы
направления
![]() и
и
![]() противоположны
изображенным на рис. 1.
противоположны
изображенным на рис. 1.
![]()
![]()
![]()
![]()

Для
того, чтобы коэффициент одной формы
найти через коэффициент другой формы,
необходимо выразить какие-либо две
одинаковые величины в этих двух формах
и сопоставить их, учтя направление токов
![]() и
и
![]() для
этих форм.
для
этих форм.
В общем
случае
![]() не равно
не равно
![]() даже по модулю.
даже по модулю.
При параллельном, последовательном и параллельно-последовательном и последовательно-параллельном соединениях необходимо соблюдать условие регулярности соединения четырехполосников - через оба первичных зажима каждого четерехполоеника должны течь равные по величине и противоположные по направлению токи, то же и по отношению к вторичным зажимам каждого четырехполосника.
Передаточная функция.
Каждое
звено можно представить в виде некоторого
четырехполосника. Входными величинами
![]() и выходными величинами
и выходными величинами
![]() могут быть разные величины (ток,
напряжение, заряд).
могут быть разные величины (ток,
напряжение, заряд).

Каковы
бы ни была схема внутренних составлений
каждого звена, всегда можно выразить
операторное изображение выходной
величины
![]() (p)
через операторное изображение входной
величины
(p)
через операторное изображение входной
величины
![]() (p)
(p)
![]()
Коэффициент пропорциональности K(p) из передаточной функцией
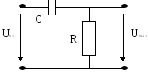
![]()
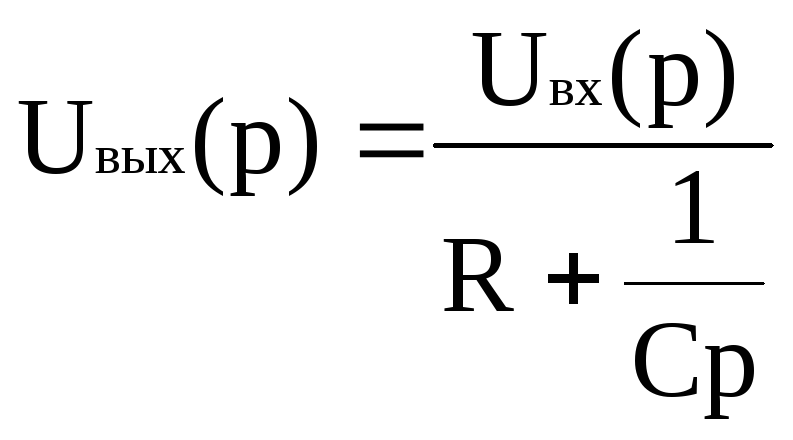
С понятием передаточной функции тесно связано понятие о частичной характеристики звена.
![]()
![]()
![]()
![]()
![]()

Электрические фильтры
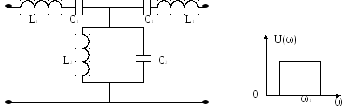
1. Назначения и типы фильтров.
Под электрическими фильтрами понимают четырехполосники, включаемые между источником питания и приемником, назначение которых состоит в том, чтобы беспрепятственно пропускать к приемнику токи одних частот и задерживать токи других частот.
Диапазон f, пропускаемы фильтром без затухания, называют полосой прозрачности; диапазон частот, пропускаемых с затуханием, - полосой затухания.
Фильтры обычно собирают по симметричной T или П -схеме.

Условимся
сопротивления
![]() в T-схеме и сопротивление
в T-схеме и сопротивление
![]() в T-схеме
называть продольными
сопротивлениями,
а
сопротивление
в T-схеме
называть продольными
сопротивлениями,
а
сопротивление
![]() в T-схеме
и сопротивление
в T-схеме
и сопротивление
![]() в П-схеме назовем поперечными
сопротивлениями.
в П-схеме назовем поперечными
сопротивлениями.
Фильтры, в которых произведение продольного сопротивления на соответ. Поперечное сопротивление представляет собой некоторое постоянное для данного фильтра число (число K), не зависящее от f, принято называть K-фильтрами. Фильтры, в которых это произведение зависит от f, m-фильтрами.
Фильтрующие свойства четырехполосников физически обусловлены возникновением в них резонансных режимов - резонансов токов или резонансов напряжений.
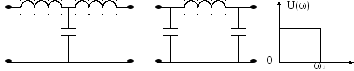
K-фильтры.
Фильтрами НЧ называются фильтры, пропускающие в нагрузку лишь
низкие
частоты с
![]() и
до
и
до
![]()
![]()
ФВЧ с
![]() до
до
![]()

Полосовой Ф с
![]() до
до
![]()
Под
заграждающими фильтрами понимают
фильтры, в которых полоса прозрачности
как бы разрезана на две части полосой
затухания 0 до
![]() и от
и от
![]() до
до
![]() .
.
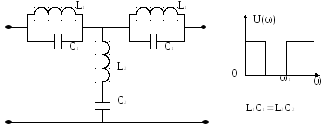
По схеме K-фильтров без проведения подробного математического анализа можно судить о том, к какому из перечисленных типов может быть отнесен тот или иной фильтр.
Если продольное сопротивление состоит только из L , то ФНЧ, если из C-то ФВЧ. Если продольное сопротивление состоит из последовательного соединения L и C , то фильтр полосового типа. Если из параллельного соединения L и C то фильтр заграждающий.
Трёхфазные цепи.
Под трёхфазной симметричной системой эдс понимают совокупность трех синусоидальных э.д.с. с одинаковой f и амплитудой, сдвинутых по фазе на 120о. Одну из эдс обозначают Еа, отстающую от нее на 120о э.д.с. – Ев, а опережающую на 120о-Ес.
Последовательность прохождения э.д.с. через одинаковые значения (например, через нулевое значение) называют последовательностью фаз.
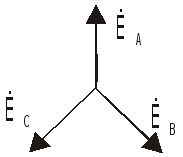
Совокупность трехфазной или нагрузок и соединительных проводов из трехфазной цепью. Токи, протекающие по отдельным участкам трехфазной цепи, сдвинуты относительно друг друга по фазе. Под фазой трехфазной цепи понимают участок трехфазной цепи, по которому протекает одинаковый ток. Под фазой будем также понимать аргумент синусоидально меняющейся величины.
Приемущества трехфазных систем.
-
передача энергии на дальние расстояния трехфазным током экономически более выгодна, чем переменным током с иным числом фаз.
-
элементы системы - трехфазный асинхронный двигатель и трехфазный трансформатор - весьма просты в производстве, экономичны и надежны в работе.
-
система обладает свойством неизменности величины мгновенной мощьности за период синусоидального тока, если нагрузка во всех трех фазах трехфазного генератора одинакова.
Существуют различные способы соединения обмоток генератора с нагрузкой. Самым неэкономичным способом явилось бы соединение каждой обмотки генератора с нагрузкой двумя проводами. В целях экономии обмотки трехфазного генератора соединяют в звезду или в ∆.

О- нулевая точка генератора.

 Пять простейших
способов соединения трехфазного
генератора с трехфазной нагрузкой.
Пять простейших
способов соединения трехфазного
генератора с трехфазной нагрузкой.
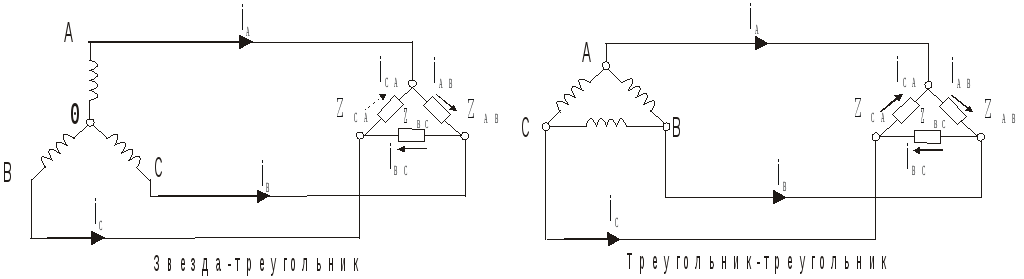
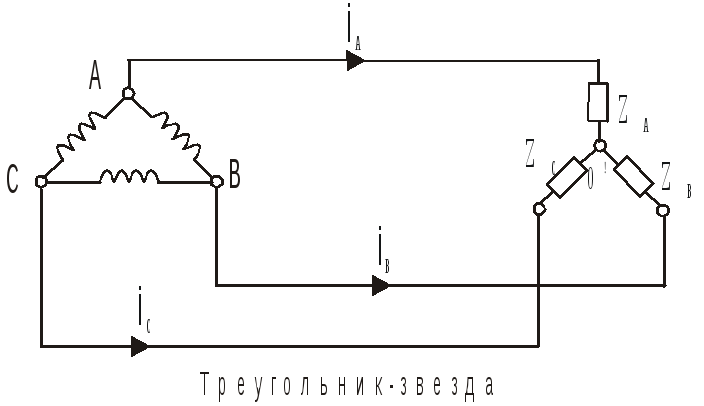
Провода, соединяющие точки А,В,С генератора с нагрузкой, называют линейными. Текущие по линейным проводам токи называются линейными. Условимся за положительное направление для них принимать направление от генератора к нагрузке. Модули линейных токов Iл. Модуль линейного напряжения Uл.
Каждую из трех обмоток генератора называют фазой генератора; каждую из трех нагрузок – фазой нагрузок; протекающие по ним токи – фазовыми токами Iф генератора или соответсвующими нагрузками, а напряжение на них – фазовыми напряжениями Uф.
При соединении
генератора в звезду линейное напряжение
в
![]() раза больше фазавого напряжения
генератора.
раза больше фазавого напряжения
генератора.
![]()
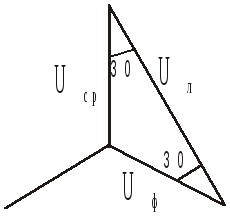
Линейный ток при соединении генератора в звезду равен фазовому току генератора. При соединении генератора в Δ Uл=Uф. При соединении нагрузки в звезду Iл=Iф. При соединении нагрузки в Δ положительные направления для токов в стороны Δ выбирают по часовой стрелке. При этом Iл ≠ Iф и определяется через них по первому закону Кирхгофа:
İА=İАВ-İСА; İВ=İВС-İАВ; İС=İАС-İВС
Если нулевой провод в схеме звезда-звезда с нулевым проводом обладает весьма малым сопротивлением, то потенциал точки 0’ практически = потенциалу точки 0. При этом в схеме образуются три обособленных контура. Точки в них равны:
![]()
По первому закону Киргофа, ток в нулевом проводе равен геометрической сумме фазовых токов
İ0 = İA+ İB+ İC.
Если нагрузка равномерна, т.е. ZA = ZB = ZC, то ток I0 = Ø и нулевой провод может быть изъят из схемы без изменения режима ее работы.
П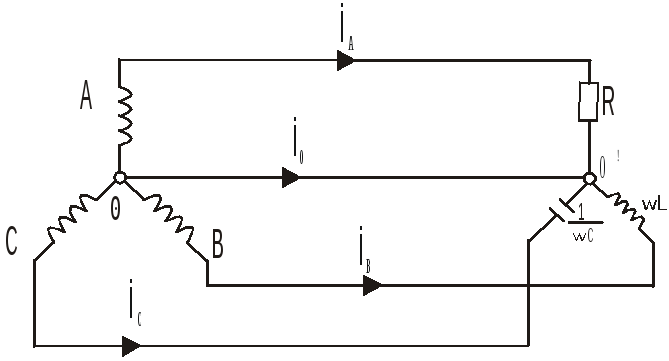 ример.
ример.
Э.Д.С. каждой фазы трехфазного генератора равна 127В. Сопротивления фаз нагрузки равны по величине 6,35 Ом, но имеют различный характер:
ZA = R, ZB=jwL, Zc= -j/wc.
Определить ток в нулевом проводе.
Токи всех фаз по модулю равны 127/6,35 =20А. Ток IA по фазе совпадает с ĖA, Ток IB на 90o отстает от ĖB. IC опережает на 90o EC.
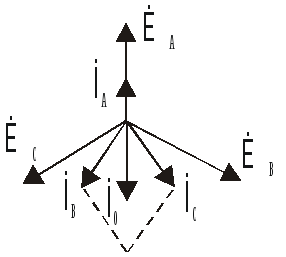
Сумма İa+İb+İc дает вектор тока İo. По модулю он равен 14,6 А.
İo=İB·![]() =İC·
=İC·![]() =20·
=20·![]() .
.
İo=İA-İo=20-20·![]() =-14,6A.
=-14,6A.
Пример.
Какой величины
должно быть взято сопротивление R
в фазе A,
чтобы ток в нулевом проводе стал = Ø?
Геометрическая сумма токов İB+İC
по модулю
равна 2.20cos30o
=20![]() .
Ток в нулевом проводе станет = Ø , если
ток İA
, направленный
противоположно сумме İB+İC
по модулю станет =20
.
Ток в нулевом проводе станет = Ø , если
ток İA
, направленный
противоположно сумме İB+İC
по модулю станет =20![]() A.
При этом сопротивление фазы А :
A.
При этом сопротивление фазы А :
R=E/20√3=127/20√3=3,66 Oм.
Пример.
Определить ток в нулевом проводе схемы, если в фазе А будет включено активное сопротивление 3,66 Ом, а индуктивность и емкость фаз В и С поменять местами.
WL=1/wc=6,35 Oм.
Векторная диаграмма.

Io=IA+IB+IC=(127/3,66)+(2∙127/6,35cos600)=20√3+2∙20∙(1/2)=34,6+34,6=69,2
