Преобразование электрических цепей

Понятие об эквивалентных преобразованиях

Анализ процессов в электрических цепях во многих случаях может быть существенно упрощен за счет использования различных преобразований, в результате которых отдельные участки идеализированных цепей заменяются другими участками, более удобными для анализа.

Два участка идеализированной электрической цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения остальной части цепи не изменяются. Преобразования электрических цепей, в результате которых некоторые участки электрической цепи заменяются эквивалентными им участками, называются эквивалентными. Из определения эквивалентных участков следует, что они должны иметь одинаковое число внешних выводов, причем в процессе эквивалентных преобразований токи этих выводов и напряжения между ними должны оставаться неизменными.

Эквивалентные участки электрических цепей обладают свойствами симметричности(если цепь А эквивалентна цепи Б, то цепь Б эквивалентна цепи А), рефлексивности(цепь А является эквивалентной самой себе) и транзитивности(если цепь А эквивалентна цепи Б, а цепь Б эквивалентна цепи В, то цепи А и В являются эквивалентными). Если эквивалентность двух участков электрической цепи выполняется при любых значениях внешних воздействий, то такие участки являются полностью эквивалентными. Различия между ними не могут быть установлены с помощью каких-либо измерений, проводимых на внешних выводах. Если эквивалентность двух участков соблюдается только при определенном значении внешних воздействий, то такие участки являются частично эквивалентными. Так, два участка линейной электрической цепи, находящейся под гармоническим воздействием, могут быть либо полностью, либо частично эквивалентными при заданной частоте внешнего воздействия.

Эквивалентные преобразования электрических цепей основаны на эквивалентных(равносильных) преобразованиях соответствующих систем уравнений электрического равновесия.

Каждое равносильное преобразование системы уравнений электрического равновесия исходной цепи (приведение подобных членов, исключение неизвестных, замена переменных и т.д.) приводит к эквивалентному преобразованию моделирующей цепи.

Соответственно изменяется и условное графическое изображение моделирующей цепи – схема цепи. На практике преобразования электрических цепей проводят без составления систем уравнений электрического равновесия, путем непосредственного преобразования схем по определенным правилам. Систему уравнений электрического равновесия цепи записывают для уже преобразованной цепи, схема которой имеет достаточно простой вид.

Участки цепей с последовательным соединением элементов

Рассмотрим неразветвленную электрическую цепь (рис. 1, а), содержащую N сопротивлений, М емкостей, К индуктивностей и V неуправляемых источников напряжения(обобщенная одноконтурная цепь). Так как через все элементы цепи протекает один и тот же ток i, то уравнение электрического равновесия, составленное на основе второго закона Кирхгофа и компонентных уравнений, может быть записано в следующем виде:

(1)

После приведения подобных членов (1) принимает вид:

, (2)

где

Уравнению (2) соответствует преобразованная цепь, схема которой изображена на рис. 1, б. Таким образом, ток и напряжение на зажимах обобщенной одноконтурной цепи не изменятся, если каждую из групп последовательно включенных однотипных элементов заменить одним эквивалентным элементом, параметр которого рассчитывается в соответствии с (2).

Из выражения (2) следует, что при последовательном включении сопротивлений, индуктивности и источников напряжения параметры эквивалентного элемента равны сумме параметров последовательно включенных элементов соответствующего типа.

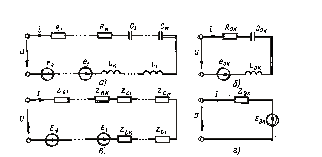
Рис. 1. Преобразование участка цепи с последовательным соединением элементов

При этом суммирование ЭДС источников напряжения производится алгебраически с учетом их знаков, которые определяются тем, совпадает или не совпадает направление ЭДС с направлением обхода контура. Очевидно, что значения или будет в N раз больше, чем параметр каждого из последовательно включенных элементов.

При последовательном включении емкостей значение величины, обратной , определяется как сумма величин, обратных каждой из последовательно включенных емкостей . Очевидно, что эквивалентная емкость будет меньше любой из последовательно включенных емкостей. При последовательном включении N одинаковых емкостей эквивалентная емкость в N раз меньше каждой из последовательно включенных емкостей.

Если обобщенная одноконтурная цепь находиться под гармоническим воздействием, то от эквивалентной схемы для мгновенных значений (рис. 1, а) удобнее перейти к эквивалентной схеме для комплексных действующих значений (рис 1, в). Уравнение электрического равновесия такой цепи, составленное на основании закона Ома и второго закона Кирхгофа в комплексной форме, имеет следующий вид:

После преобразования получаем

(3)

где

Комплексная схема замещения цепи, соответствующая уравнению (3), приведена на рис 1, г.

Таким образом, любой участок электрической цепи, представляющий собой последовательное соединение произвольного числа идеализированных неуправляе­мых источников напряжения и пассивных двухполюсников, при гармоническом воздействии может быть заменен ветвью, содержащей один источник напряжения, ЭДС которого равна алгебраической сумме ЭДС всех последовательно включенных источников, и один пассивный двухполюсник, комплексное сопротивление которого равно сумме комплексных сопротивлений всех последовательно включенных пассив­ных двухполюсников.

Участки цепей с параллельным соединением элементов

Пусть электрическая цепь (2, а) состоит из параллельно соединенных N сопротивлений, M емкостей, К индуктивностей и v неуправляемых источников тока (обобщенная двухузловая цепь). Все элементы цепи находятся под одним и тем же напряжением u, поэтому уравнение электрического равновесия, составленное на основании первого закона Кирхгофа, может быть записано в виде:

(4)

После приведения подобных членов получаем

(5)

где

Уравнению (5) соответствует преобразованная цепь, схема которой приведена на рис. 2, б. Очевидно, что ток и напряжение на зажимах обобщенной двухузловой цепи не изменяется, если каждую из групп параллельно включенных однотипных элементов заменить одним эквивалентным элементом, параметры которого рассчитываются в соответствии с (5).

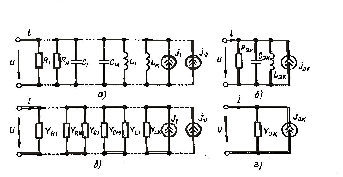
Рис. 2. Преобразование участка цепи с параллельным соединением элементов

Из выражения (5) следует, что при параллельном включении емкостей и источников тока параметры эквивалентного элемента равны сумме параметров параллельно включенных элементов соответствующего типа. При этом суммирование токов источников тока производится алгебраически с учетом их знаков, определяемых ориентацией источников относительно узла, для которого составляется уравнение (5). Очевидно, что превышает по значению любую из параллельно включенных емкостей . При параллельном соединении N одинаковых емкостей .

При параллельном включении сопротивлений или индуктивностей значения величин, обратных и , определяются как сумма значений всех величин, обратных параллельно включенным сопротивлениям или индуктивностям .

Очевидно, что значения будут меньше, чем сопротивление или индуктивность любого из параллельно включенных элементов соответствующего типа. При параллельном включении N одинаковых сопротивлений R или индуктивностей L а .

Для рассмотрения параметров обобщенной двухузловой цепи при гармоническом воздействии воспользуемся комплексной схемой замещения этой цепи (рис. 2, в). Уравнение электрического равновесия цепи в комплексной форме может быть записано следующим образом:

или (6)

где

Комплексная схема замещения цепи, соответствующая уравнению (6), изображена на рис. 2, г.

Таким образом, любой участок электрической нош, представляющий собой параллельное соединение произвольного числа идеализированных пассивных двухполюсников, может быть эаменен одним пассивным двухполюсником, комплексная проводимость которого равна сумме комплексных проводимостей всех параллельно включенных двухполюсников. Произвольное число параллельно включенных иде­ализированных источников тока может быть заменено одним источником, комплексное действующее значение тока которого равно алгебраической сумме комплексных действующих значений токов всех параллельно включенных источников.

Переходя в (6) от комплексных проводимостей к комплекс­ным сопротивлениям, находим эквивалентное комплексное входное сопротивление группы параллельно включенных идеализирован­ных пассивных двухполюсников:

(7)

Выражения, подобные (6) и (7), можно получить для комплексной проводимости и комплексного сопротивления любого участка цепи, являющегося, параллельным соединением произволь­ного числа идеализированных пассивных двухполюсников с задан­ным комплексным входным сопротивлением , или комплексной входной проводимостью :

(8)

где N — число параллельно включенных двухполюсников.

Используя (8), получим выражение для комплексного вход­ного сопротивления участка цепи, представляющего собой парал­лельное соединение двух элементов с комплексными сопротивлени­ями :

(9)

Участки цепей со смешанным соединением элементов

Правила преобразования участков цепей с параллельным или последовательным соединением элементов могут быть применены и для преобразования пассивных участков цепей со смешанным соединением элементов. Преобразование таких участков, представ­ляющих собой сочетание групп параллельно или последовательно включенных элементов, обычно производят в несколько этапов, на каждом из которых группу параллельно включенных элементов заменяют одним двухполюсником, комплексная проводимость ко­торого равна сумме комплексных проводимостей параллельно включенных элементов, а группу последовательно включенных эле­ментов — одним двухполюсником, комплексное сопротивление ко­торого равно сумме

комплексных сопротивлений всех последовате­льно включенных элементов.

Пример 1. Рассмотрим преобразование участка идеализированной цепи со смешанным соединением элементов (рис. 3, а), содержащего группу параллельно включенных элементов и группу последовательно включенных элементов

Заменяя параллельно включенные элементы одним элементом с комп­лексным сопротивлением получим преобразованную схему цепи (рис.3, б) с тремя последовательно включенными элементами . Вводя вместо этих элементов один с комплексным сопротивлением приходим к простейшей преобразо­ванной схеме рассматриваемого участка цепи с одним элементом (рис. 3, в).

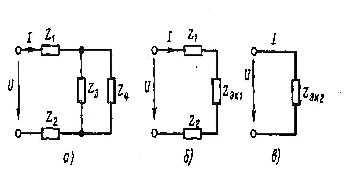
Рис. 3. К примеру 1

Пример 2. Определим эквивалентную индуктивность цепи при мкГн (рис. 4).

Участок цепи с тремя параллельно включенными одинаковыми индуктивностями обладает эквивалентной индуктивностью, в три раза меньшей, чем каждая из параллельно включенных индуктивностей: мкГн. Этот участок включен последовательно с индуктивностью поэтому искомая эквивалентная индуктивность мкГн.

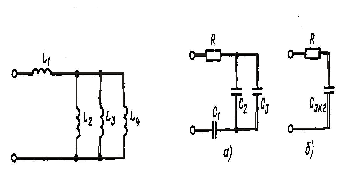
Рис. 4. К примеру 2 Рис. 5. К примеру 3

Пример 3 Найдем комплексное входное сопротивление участка цепи с параметрами элементов R=1.5 кОм, =40 пФ, =10 пФ, =50 пФ на частоте МГц (рис. 5, а).

Параллельно включенные емкости и могут быть заменены одной экви­валентной емкостью 60 пФ.

Емкости и , включенные последовательно, заменим одной емкостью =24 пФ. Получаем преобразованную цепь (рис. 5, б) комплексное входное сопротивление которой на частоте МГц

кОм

Таким образом, в результате объединения групп последовательно и параллельно включенных элементов происходит постепенное сворачивание цепи, причем участок со смешанным соединением пассивных элементов, имеющий два внешних вывода (пассивный двухполюсник), в конечном счете может быть заменен одним элементом, комплексное сопротивление которого равно входному сопротивлению данного участка цепи.

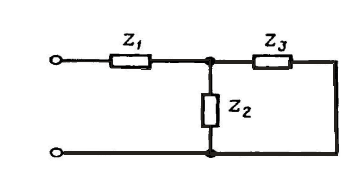
Рис. 6. Схема простейшей лестничной цепи

К цепям со смешанным соединением элементов относятся цепные, или лестнич­ные, цепи, входное сопротивление или входная проводимость которых могут быть представлены в виде цепной (непрерывной) дроби, т. е. с помощью выражения типа

(10)

Коэффициенты называются элементами цепной дроби. Число элементов дроби N может быть конечным (конечная цепная дробь) или бесконечным (бесконечная цепная дробь).

Для удобства изображения условимся записывать цепную дробь (10) в виде

(11)

Рассмотрим простейшую лестничную цепь (рис 6) Нетрудно установить, что входное сопротивление этой цепи

Заменяя в этом выражении сопротивление элемента его проводимостью окончательно получаем:

или в форме (11)

Таким образом, входное сопротивление рассматриваемой цепи может быть представлено в виде конечной цепной дроби, элементы которой равны соответственно . Используя аналогичные преобразования, можно представить в виде цепной дроби и входное сопротивление лестничной цепи более общего вида (рис. 7, а):

(12)

Как следует из (12), число элементов цепной дроби равно числу идеализированных двухполюсных элементов, образующих лестничную цепь, причем элементами дроби являются комплексные сопротивления двухполюсников, образующих продольные ветви ле­стничной цепи и комплексные проводимости двухпо­люсников, входящих в поперечные ветви .

Если лестничная цепь содержит поперечную ветвь, подключен­ную непосредственно к внешним зажимам цепи (рис. 7, б), то в виде цепной дроби может быть представлена входная проводи­мость:

(13)

Таким образом, для того чтобы выражения для входных со­противлений или входных проводимостей лестничных цепей могли быть записаны в виде цепных дробей типов (12), (13), необ­ходимо элементы, образующие продольные ветви, представить их комплексными сопротивлениями, а элементы, входящие в попереч­ные ветви,— их комплексными проводимостями.

Для определения тока или напряжения произвольной ветви лест­ничной цепи (рис. 7) по заданному значению напряжения U или тока I на входе этой цепи можно воспользоваться простым при­емом, известным из литературы как метод пропорциональных вели­чин (метод пропорционального пересчета, метод единичного тока, метод подобия). В соответствии с этим методом ток N-й ветви(наиболее удаленной от входных зажимов) обозначим, например, .

Выразим через напряжение N-й ветви , ток и напряжение N-2 ветвей:

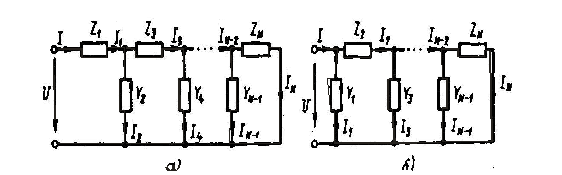
Рис. 7. Схема лестничных цепей общего вида

и т.д вплоть до напряжения и тока первой ветви. Так как рассматриваемая цепь является линейной, то напряжение и токи всех ветвей окажутся прямо пропорциональными . В том случае, когда заданным является напряжение на U входе цепи, ток определим, приравнивая напряжение U сумме напряжений первой и второй ветвей (рис. 7, а) или напряжению первой ветви (рис. 7, б). Если задано комплексное действующее значение тока на входе двухполюсника I, ток находим, приравнивая ток I току первой ветви (рис. 2.38, а) или сумме токов первой и второй ветвей (рис. 7, б). Подставляя полученное значение в выражение для тока или напряжения интересующей ветви, выражаем искомую величину через напряжение или ток на входе цепи.

Пример 4. Найдем ток i через входные зажимы цепи, схема которой приведена на рис. 8. Параметры элементов:

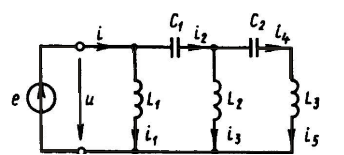
Рис. 8. К примеру 4

задача может быть решена двумя способами.

1. Определим комплексную входную проводимость цепи с помощью (13):

См.

Комплексное действующее значение тока находим, используя закон Ома в комплексной форме:

мА,

откуда

мА.

2. Обозначим комплексное действующее значение тока пя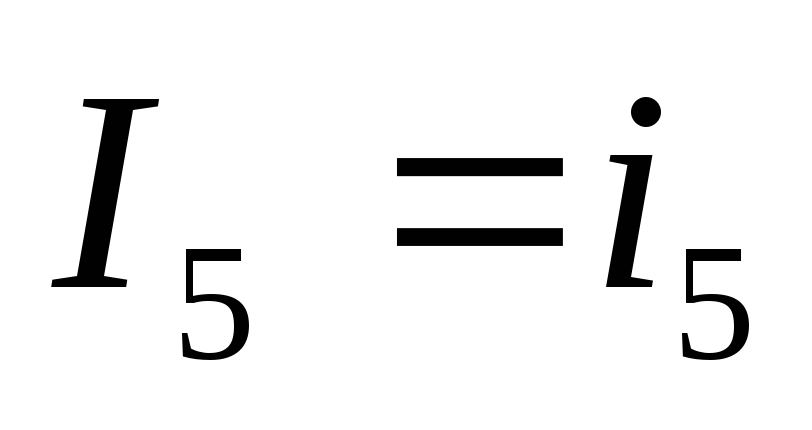той ветви . Комплексное действующее значение напряжения этой ветви

Выражаем через комплексные ток и напряжение:

четвертой ветви

третьей ветви

второй ветви

первой ветви

и комплексное напряжение и ток на входе цепи

Принимая во внимание, что комплексное действующее значение напряжения на входе цепи известно (U=E=50 В), определяем комплексное действующее значение тока пятой ветви:

мА.

Подставляя значение в найденные ранее выражения, получаем комплексные ток и напряжение любой ветви рассматриваемой цепи. В частности, комплексное действующее значение входного тока цепи

мА,

откуда

мА.

Преобразование звезды в треугольник и треугольника в звезду

Соединение трех сопротивлений, имеющее вид трехлучевой звезды, называется соединением звезда, а соединение трех сопротивлений так, что они образуют собой стороны треугольника – соединением треугольника.

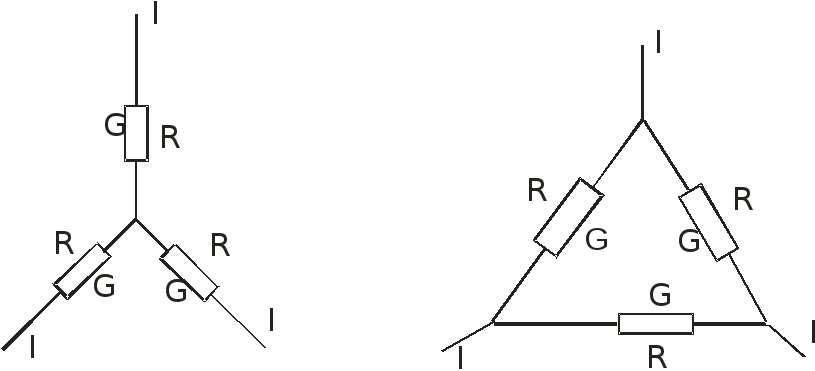
Очень часто при расчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи будут одинаковы, то вся внешняя схема «не заметит» произведенной замены.

Для звезды:

(14)

Для треугольника:

(15)

Так как ток в схеме звезды должен равняться току в схеме треугольника при любых значениях потенциалов , то коэффициент при в правой части (15) должен равняться коэффициенту при в правой части (14), а коэффициент при в правой части (15) должен равняться коэффициенту при в правой части (14).

Последние формулы дают возможность найти проводимости сторон треугольника через проводимости лучей звезды.

; ; ;

; ; ;

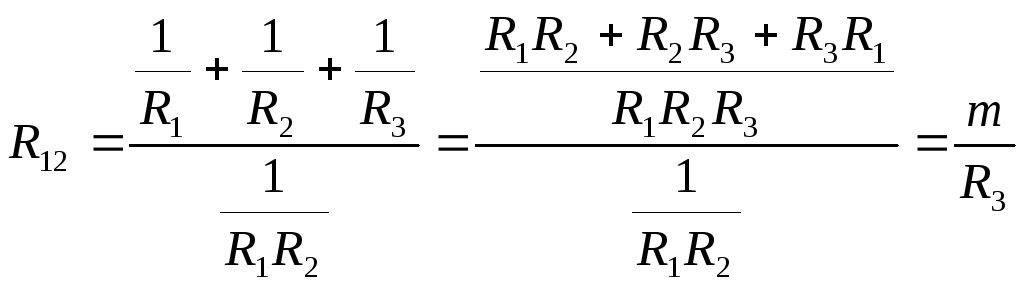(16)

(17)

(18) (19)

Подставив (16), (18) и (19) в (17), получим

; ;

Периодические несинусоидальные токи в линейных электрических цепях

Периодическими несинусоидальными токами и напряжениями называют токи и

Напряжения, изменяющиеся во времени по периодическому несинусоидальному закону.

Из курса математики известно, что любую периодическую функцию f(x) с периодом

2 можно разложить в ряд Фурье.

Переменная величина x связана со временем t соотношением х = t=2

Ряд Фурье записывают так: f(x)=A₀ + +

A₀-постоянная составляющая

-амплитуда синусной составляющей первой гармонии

-амплитуда косинусной составляющей первой гармонии

-амплитуда синусной составляющей второй гармонии и т.д.

A₀=

Так как =sin k x + cos k x =A_k sin (k x+),

Где и

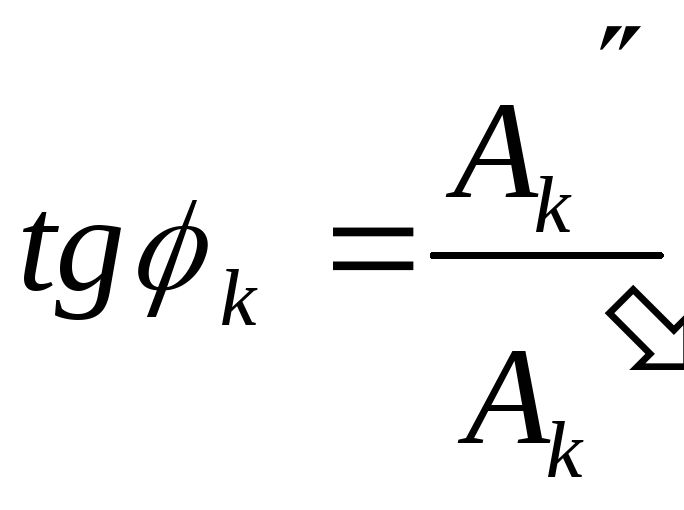
То ряд Фурье можно записать в другой форме f(x)=A₀+A₁ sin (x +₁)+A₂ sin(2x+₂) +…=

=A₀+A_k sin (k x+_k).

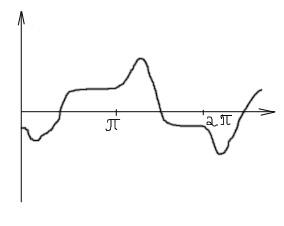
Кривая удовлетворяет условию –f(x+)=f(x).

Симметричная относительно оси абсцисс.

При разложении таких кривых в ряд Фурье отсутствуют постоянная составляющая и четные гармонии … 0 f(x)=

Симметричная относительно оси ординат f(-x)= f(x)

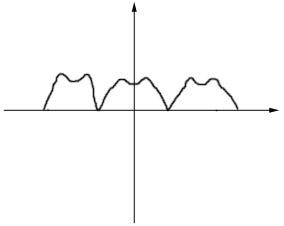
В разложении таких кривых в ряд Фурье отсутствуют синусоидальные составляющие,

т.е.

f(x)=

Симметричная относительно начала координат –f(-x) = f(x)

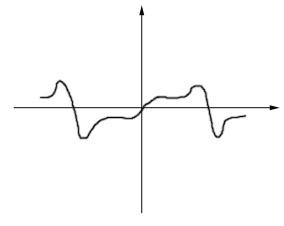
В разложении таких кривых в ряд Фурье отсутствуют косинусные составляющие

Определение гармонии ряда Фурье основано на замене определенного интеграла суммой конечного числа слагаемых. С этой целью период функции f(x) ,равный 2,

разбивают на n равных частей и интегралы заменяют суммами .

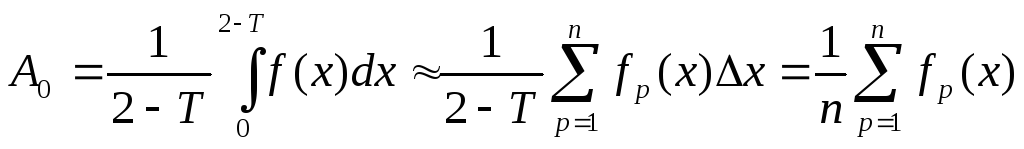
где f p(x) – значение функции f(x) при x=(p-0,5)∆ x, т.е. в середине p-го интервала.

Пример: Найти первые 3 гармонии и постоянную составляющую функции f(x),симметричную относительно оси абсцисс. Значения ординат за первый полупериод при разбивании периода n= 24 части следующие

p = 1 2 3 4 5 6 7 8 9 10 11 12

f p(x)= 7 11 13,5 15,4 17,4 20,5 25,4 32,5 27,7 19,2 10 5

Т.к. кривая симметрична относительно оси абсцисс, то А₀ =

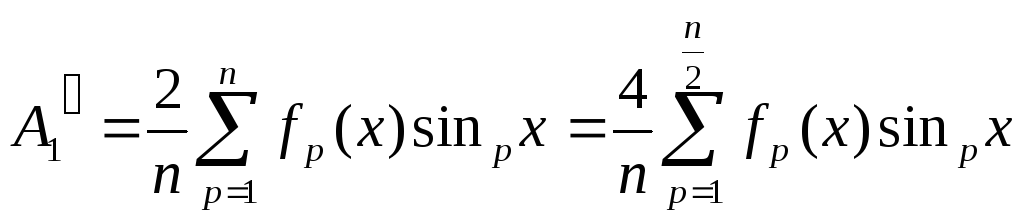
(7 sin 7º 30' + 11sin 22º 30' + 13,5 sin 37º 30' + 15,4 sin 52º 30' + 17,4 sin 67º 30' + 20,5 sin 82º 30' + 25,4 sin 97º30' + 32,5 sin 112º30' + 27,7 sin 127º 30' + 19,2 sin 142º 30' + 10 sin 157º 30' + 5 sin 172º 30' )  25,4

-5,23 3,47 5,1

Амплитуда первой гармонии

А =

tg ₁ =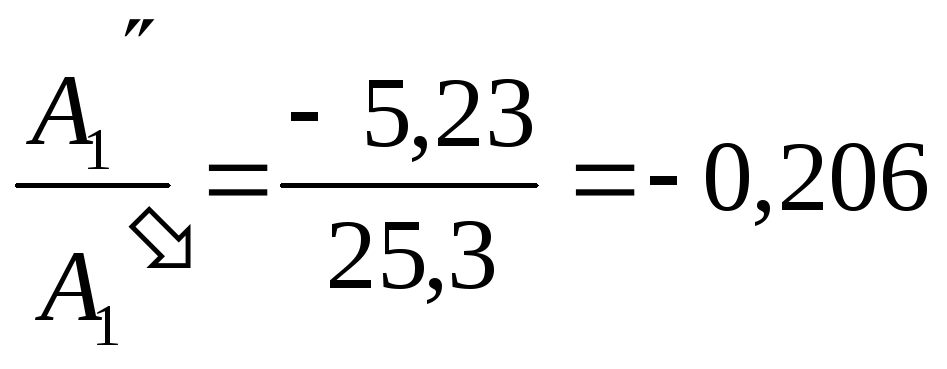 ₁ = -11º40'

A₃= 6 ₃ =55º50'

f(  t )= 25,9 sin (  t - 11º40' ) + 6sin (3 t + 55º 50' )

Для проведения расчета ток или напряжение должны быть представлены рядом Фурье. Согласно принципу наложения, мгновенное значение тока любой ветви схемы равно сумме мгновенных значений тонов отдельных гармоник.(так же и напряжение). Расчет производят для каждой из гармоник в отдельности.

Сначала рассчитывают токи и напряжения, возникающие от действия постоянной

составляющей э.д.с. , или источника тока , после этого – токи и напряжения от действия первой гармонии , затем от второй гармонии , от третьей и т.д. .

При расчете токов и напряжений , возникающих от действия постоянной составляющей э.д.с. , необходимо иметь в виду , что падение напряжения на индуктивности L от постоянного тока равна нулю , а также что постоянный ток через емкость С не проходит.

При расчете следует учитывать, что индуктивное сопротивление прямо ~ частоте; по этому для k-гармоники X_LK в k раз больше, чем для первой гармоники X_L1.

X_LK= kwL= k X_L1

Емкостное сопротивление уменьшается с ростом частоты; поэтому для k-гармоники X_CK в k раз меньше, чем для первой гармоники.

Резонансный режим работы – ток совпадает по фазе с э.д.с.

Если воздействующая э.д.с. не синусоидальна, то в электрической цепи могут возникнуть резонансные режимы не только на первой гармонике, но и на высших гармониках.

Резонанс на k-гармонике I_K cовпадает по фазе с U_K, а I_i не совпадает с U_i .

Исследование резонансных явлений при несинусоидальных токах часто производят, полагая активные сопротивления индуктивных катушек равными нулю.

В этом случае входное сопротивление при резонансе токов равно , а сопротивление при резонансе напряжений равно нулю.

При возникновении резонансного режима на какой-либо высшей гармонике токи и напряжения этой гармоники могут оказаться большими, чем токи и напряжения первой гармоники на участке цепи, несмотря на то , что амплитуда соответствуютщей высшей гармоники э.д.с. на входе схемы может быть в несколько раз меньше амплитуды первой гармоники э.д.с.

Пример

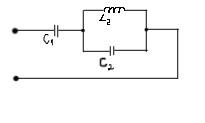
Задана индуктивность L₂. Полагая активное сопротивление индуктивной катушки равным нулю. Найти, при каких значениях емкостей и входное С₁ и С₂ сопротивление схемы для первой гармоники равняется нулю, а для девятой гармоники равно бесконечности.

Входное сопротивление схемы для первой гармоники

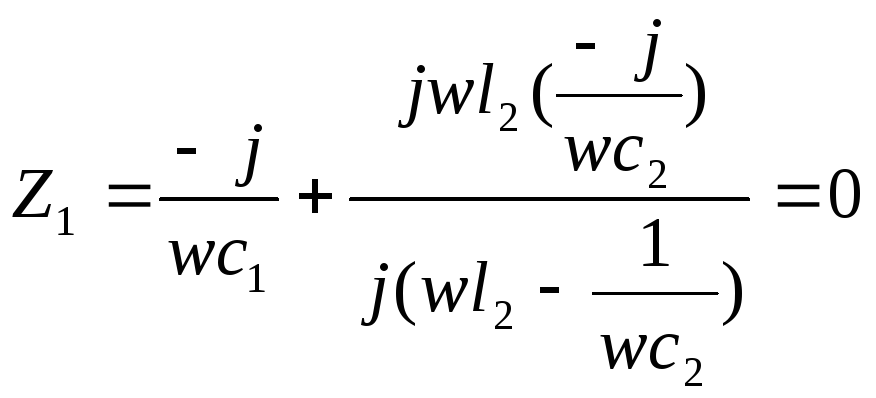
Входное сопротивление для девятой гармоники.

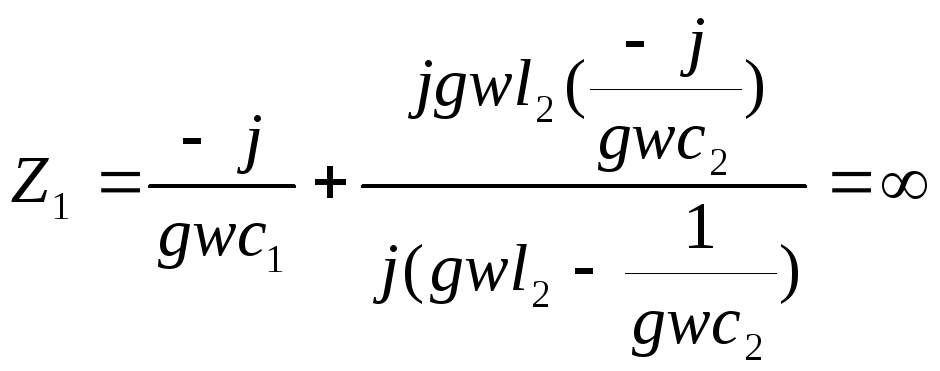
Совместное решение дает

Действующее значение тока

i = I₀ + I_1m sin ( t +₁ )+ I_2m sin ( 2 t+₂ ) +… .

то

Но

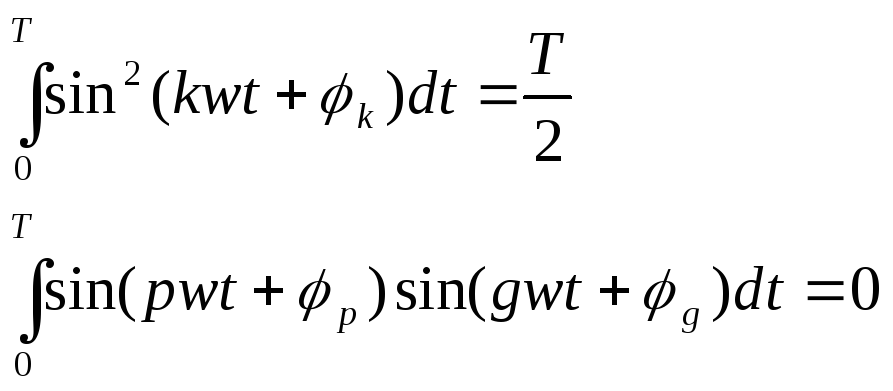
Поэтому

Или

Так как амплитуда k–гармоники тока I_km в  2 раз больше действующего значения k-гармоники I_R, то и

Под активной мощностью P несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники

Если представить напряжение и ток рядом Фурье

P =I₀U _I + I₁U _I cos₁ + U _I I₂cos₂ +…

Активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник.

Нелинейные электрические цепи постоянного тока.