Связанные колебательные контуры общие сведения

Два контура называются связанными, если возбуждение электрических колебаний в одном из них приводит к возникновению колебаний в другом. Каждый из связанных контуров может быть либо колебательным (если он содержит индуктивные катушки и конденсаторы), либо апериодическим (если он содержит реактивные элементы только одного типа). Наибольший практический интерес представляют связанные колебательные контуры, так как их избирательные свойства лучше, чем избирательные свойства одиночных колебательных контуров.

В зависимости от типа элемента, с помощью которого осуществляется взаимодействие между контурами, различают контуры с трансформаторной, индуктивной, емкостной и комбинированной (индуктивно-емкостной) связями. По способу включения элемента связи связанные контуры подразделяются на контуры с внешней и внутренней связями. Принципиальные электрические схемы связанных колебательных контуров некоторых типов приведены на рис. 3. 42.

Внешнее воздействие на связанные колебательные контуры обычно задается в виде напряжения источника энергии Г, включенного в один из контуров, называемый первичным. В качестве реакции связанных контуров на внешнее действие рассматривают ток или напряжение одного из элементов другого контура, называемого вторичным.

Каждому типу связанных колебательных контуров можно поставить в соответствие так называемый четырехполюсник связи (рис.3.43), который получается из исходных контуров при их размыкании устранении из них всех элементов, имеющих другой характер по сравнению с элементом связи.

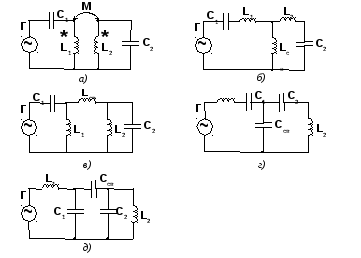
Рис. 3.42. Принципиальные электрические схемы связанных колебательных контуров:

а — с трансформаторной связью; б — с внутренней индуктивной (автотрансформаторной) связью; в — с внешней индуктивной связью; г — с внутренней емкостной связью; д — с внешней емкостной связью

Рис. 3.43. Четырехполюсники связи, соответствующие контурам, приведенным на рис. 3.42

Назовем коэффициентом передачи из первичного контура во вторичный К₂₁ комплексный коэффициент передачи соответствующего четырехполюсника связи по напряжению от зажимов 1 — 1’ к зажимам 2— 2’ (при холостом ходе на зажимах 2 — 2’)

а коэффициентом передачи из вторичного контура в первичный — комплексный коэффициент передачи четырехполюсника связи по напряжению от зажимов 2 — 2’ к зажимам 1 — 1’ (при холостом ходе на зажимах 1 — 1’)

Нетрудно убедиться, что коэффициенты передачи К₁₂ и К₂₁ связанных контуров, схемы которых приведены на рис. 3. 42, а — д, а соответствующие четырехполюсники связи — на рис. 3. 43, а — д, являются действительными числами и не зависят от частоты.

Среднее геометрическое из коэффициентов передачи К₁₂ и К₂₁ называется коэффициентом связи между контурами

(3.105)

Коэффициент связи не зависит от частоты и используется для количественной оценки степени связи между контурами.

Для контуров с трансформаторной связью (см. рис. 3. 42, а) при определении коэффициентов передачи К₁₂ и К₂₁ можно воспользоваться компонентными уравнениями связанных индуктивностей (2. 172):

(3.106)

Подставляя выражение (3. 106) в (3. 105), можно установить, что коэффициент связи между контурами с трансформаторной связью равен коэффициенту связи между входящими в эти контуры индуктивностями:

(3.107)

Анализируя четырехполюсники связи, получим выражения для коэффициентов связи между контурами:

с внутренней индуктивной (автотрансформаторной) связью (см. рис. 3. 42, б)

(3.108)

с внешней индуктивной связью (см. рис. 3. 42, в)

(3.109)

с внутренней емкостной связью (см. рис. 3.42, г)

(3.110)

и с внешней емкостной связью (см. рис. 3.42, д)

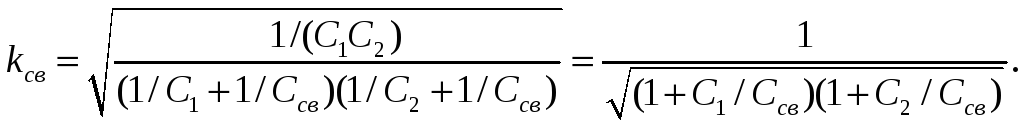
(3.111)

Из выражений (3.107) — (3.111) следует, что значение коэффициента связи между контурами k_св не может превышать единицы, причем с увеличением параметра элемента связи (M, L_св, С_св) возрастает коэффициент k_св между контурами с трансформаторной, автотрансформаторной и внешней емкостной связями и уменьшается коэффициент связи между контурами с внешней индуктивной и внутренней емкостной связями.