
- •Екзаменаційні питпння за курсом «тау – частина1»
- •1. Дайте визначення поняття керування?
- •2. Які алгоритми роботи об’єктів курування вам вібомі?
- •3. Що нази вається вектором вихідного стану об’єкта керування?
- •4. Що називаться структурною схемою сау?
- •5. Класифікація систем автоматичного керування?
- •6. Що називається помилкою керування?
- •7. Назвіть основні причини відхилення вектора вихідного стану від необхідного значення?
- •8. Для яких цілей необхідні керуючі впливи?
- •9. Що називаеться керуючим пристроєм?
- •10. Що називається системою автоматичного керування?
- •11. Які принципи керування вам відомі?
- •12. Яка сау називається замкнутою?
- •13. У чому складаеться сутність принципу керування по збурюванню?
- •14. Основні переваги і недоліки сау, побудоватних на бузі принципу керування по збурюванню?
- •15. У чому полягає сутність керування по відхиленню?
- •16. Для яких цілей використовується зворотний зв’язок у сау? Які види зворотних зв’язків вам відомі?
- •17. У чому полягають основні особливості принципу комбінованого керування?
- •18. Які основні переваги і недоліки сау з комбінованим керуванням Вам відомі?
- •19. Що називається статичною характеристикою сау і її елементів?
- •20. Які види статичних характеристик сау Вам відомі?
- •21. Які особливості властиві астатичним елементам?
- •22. Дайте визначення сатичної сау?
- •23. Дайте визначення астатичної сау?
- •24. Які способи з’єднання елементів сау вам відомі?
- •25. Як визначити статичну характеристику сау, що складається з послідовно з’єднаних елементів?
- •26 Як визначити статичну характеристику сау, що складається з паралельно з’єднаних елементів?
- •27. Як визначити статичну характеристику сау при з'єднанні лементів з використанням зворотного зв'язка?
- •28. Для яких цілей використається лінеаризація статичних характеристик сау?
- •29. Опишіть основні принципи лінеаризації статичних характеристик сау?
- •30. Що розуміється під поняттям динамічні режими роботи сау?
- •31.Який математичний апарат використається для аналізу динамічних
- •33. Як представити рівняння руху сау у формі Коші?
- •34.Які методи рішення диференціальних рівнянь Вам відомі?
- •35. Що називається перетворенням Лапласа. Як воно виробляється?
- •36. Які основні властивості перетворення Лапласа Вам відомі?
- •37.Що називається передатною функцією сау?
- •38. Що називається характеристичним рівнянням системи?
- •39. Частотні характеристики сау і їхнє експериментальне визначення?
- •40. Змінні стани і рівняння стану динамічної системи?
- •41. Типові динамічні ланки і їхні рівняння, передатні функції, тимчасові і частотні характеристики?
- •42. Правила структурних перетворень сау і визначення передатних функцій складних систем?
- •43.Застосування теорії графів для визначення передатних функцій складних багатоконтурних сау?
- •44. Прямі показники якості перехідних процесів?
- •45. Оцінка якості перехідних процесів по частотних характеристиках?
- •46. Кореневі критерії оцінки якості перехідних процесів?
- •47. Інтегральні методи оцінки якості перехідних процесів?
- •48. Характеристики основних елементів сау: тиристорний перетворювач, широтно-імпульсний перетворювач, датчик струму, датчик швидкості, електродвигун постійного струму, асинхронний двигун?
- •49. Стійкість сау. Алгебраїчні критерії стійкості?
- •50. Стійкість сау. Частотні критерії стійкості?
- •51. Статистичні характеристики сау і зв'язок між ними?
- •52. Комбіновані аср. Принцип інваріантості?
- •53. Каскадні аср. Розрахунок каскадних аср?
- •54. Взаємозалежні системи регулювання. Методи розрахунку зв'язаних систем регулювання. Принцип автономності?
- •55. Регулювання об'єктів із запізнюванням?
- •56. Системи регулювання нестаціонарними об'єктами?
- •57. Робастні системи керування і чутливість?
- •58. Синтез сау методом логарифмічних частотних характеристик для об'єктів з астатизмом другого порядку?
- •59. Синтез сау методом логарифмічних частотних характеристик для об'єктів з астатизмом першого порядку?
- •60. Синтез сау методом логарифмічних частотних характеристик для статичних об'єктів?
- •61. Експрес методи розрахунку настроювання одно контурних систем регулювання?
- •62. Модальне керування в сау?
- •63. Синтез систем керування з регулятором стану?
- •Екзаменаційні питпння за курсом «тау – частина2»
- •2. Нелінійні характеристики (однозначні, неоднозначні) і їхній математичний опис.
- •3. Методи лінеаризації нелінійних характеристик.
- •4. Дослідження нелінійних систем (метод гармонійного балансу).
- •5. Дослідження нелінійних систем (метод фазових траєкторій).
- •6. Нелінійні системи (побудова перехідного процесу по фазовій траєкторії).
- •7. Нелінійні системи (побудова фазових траєкторій методом ізоклін).
- •8. Нелінійні системи (знаходження результуючої статичної характеристики при паралельному, послідовному, зустрічно-паралельному з'єднанні нелінійних елементів).
- •9. Методи дослідження стійкості нелінійних систем. Другий (прямій) метод Ляпунова.
- •10. Методи дослідження стійкості нелінійних систем. Критерій абсолютної стійкості в.М. Попова.
- •11. Поняття про дискретні системи автоматичного керування і їхня класифікація.
- •12. Релейні системи автоматичного керування. Визначення, особливості, призначення, достоїнства й недоліки.
- •13. Особливості динаміки релейних систем автоматичного керування.
- •14. Фазові портрети релейних систем.
- •15. Імпульсні системи автоматичного керування. Визначення, особливості, призначення, класифікація, достоїнства й недоліки.
- •16. Особливості динаміки імпульсних систем автоматичного керування.
- •17. Математичний апарат імпульсних систем (ґратчаста функція, зміщена ґратчаста функція).
- •18. Математичний апарат імпульсних систем (різниця ґратчастих функцій, різницеві рівняння).
- •19. Математичний апарат імпульсних систем (z-перетворення і його основні властивості).
- •20. Передатні функції імпульсного фільтра.
- •21. Цифрові системи автоматичного керування. Визначення, особливості, призначення, достоїнства.
- •23. Опишіть типову структуру одно контурної сау.
- •29. Розрахунок помилок у цас.
- •30. Способи побудови перехідних процесів у цас.
- •31. Порядок синтезу цсу для об'єктів з астатизмом другого порядку.
- •32. Порядок синтезу цсу для об'єктів з астатизмом першого порядку.
- •34. Модальне керування в цсу.
- •35. Поняття оптимальної системи автоматичного керування.
- •36. Послідовність проектування оптимальної сау.
- •45. Класифікація адаптивних і самонастроювальних систем.
- •46. Самонастроювальні сау з оптимізацією статичних режимів.
- •47. Самонастроювальні сау з оптимізацією динамічних режимів.
- •48. Методи пошуку екстремуму функції настроювальних параметрів.
- •49. Найпростіша що самоорганізується сау.
- •50. Поняття про системи, що самонавчаються, автоматичного керування.
41. Типові динамічні ланки і їхні рівняння, передатні функції, тимчасові і частотні характеристики?
Большинство сиcтем может быть представлено совокупностью относительно звеньев с передаточными функциями невысокого порядка. Такие звенья называются типовыми.
Типовым называется такое звено, которое описывается дифференциальным уравнением не выше второго порядка. К таким звеньям относятся:
-
безинерционное звено – звено нулевого порядка,
-
апериодическое звено – звено первого порядка,
-
интегрирующее звено – звено первого порядка,
-
дифференциальное звено – звено первого порядка,
-
колебательное звено – звено второго порядка.
Безинерционное звено.
Уравнение движения для безинерционного звена имеет вид
![]() .
.
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
![]()
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как
![]() .
.
Выполняя обратное
преобразование изображения переходной
характеристики
![]() ,
получаем:
,
получаем:
![]()
Выполняя
аналогичные преобразования над
изображением весовой функции, получаем
выражение для определения весовой
функции
![]() .
.
![]()
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
![]()
Исходя из этого, амплитудно-частотная характеристика звена представляется точкой на комплексной плоскости.
Логарифмическая частотная характеристика представляется прямой параллельной оси частот. Это следует из выражения для определения логарифмической частотной характеристики вида:
![]() .
.
Апериодическое звено
Уравнение движения для безинерционного звена имеет вид
![]() .
.
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
![]()
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как
![]() .
.
Корни
характеристического уравнения
![]() определяются
как
определяются
как
![]() .
.
Выполняя обратное
преобразование изображения переходной
характеристики
![]() получаем:
получаем:
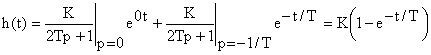 .
.
Выполняя аналогичные преобразования над изображением весовой функции
![]()
получаем выражение
для определения весовой функции
![]() .
.

Переходная и весовая характеристики звена приведены на рис. 5.
T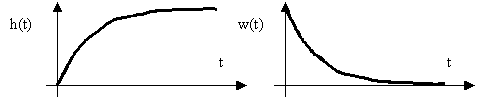
Рис. 5. Временные характеристики апериодического звена.
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
![]()
Исходя из этого, амплитудно-частотная характеристика звена определяется как:
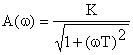 .
.
Вещественная
![]() и
мнимая
и
мнимая
![]() частотные
характеристики звена определяются как
частотные
характеристики звена определяются как
![]()
![]()
АФЧХ звена определяется как
![]()
Выражение для расчета ЛАЧХ принимает вид:
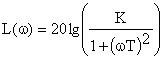 .
.
![]() .
.
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
 .
.
На рис. 6 приведены амплитудно-фазовая и логарифмическая частотные характеристики безинерционного звена.
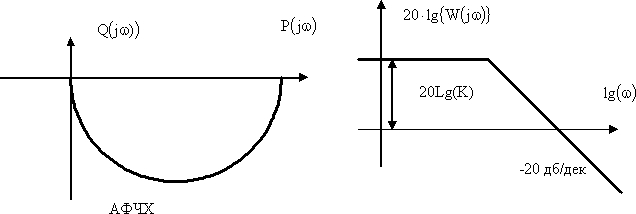
Рис. 6. Амплитудно-фазовая частотная и логарифмическая частотные характеристики апериодического звена
Интегрирующее звено
Уравнение движения для интегрирующего звена имеет вид
![]()
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
![]()
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика звена определяется как
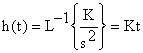 .Весовая
характеристика определяется как
.Весовая
характеристика определяется как
![]() .
.
Эти характеристики интегрирующего звена приведены на рис. 7.
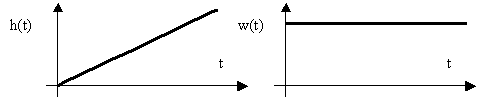
Рис. 7. Временные характеристики интегрирующего звена
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
![]()
Исходя из этого, амплитудно-частотная характеристика звена определяется как:
![]()
Вещественная
![]() и
мнимая
и
мнимая
![]() частотные
характеристики звена определяются как
частотные
характеристики звена определяются как
![]() .
.
![]()
Выражение для расчета ЛАЧХ принимает вид:
![]()
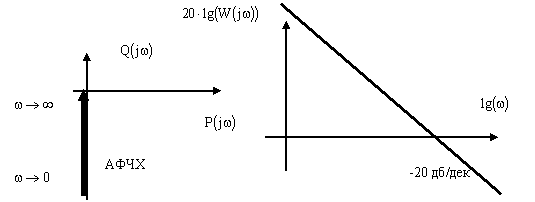
Рис. 8. Амплитудно-фазовая частотная и логарифмическая частотные характеристики звена.
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
![]() .
.
Амплитудно-фазовая и логарифмическая частотные характеристики звена показаны на рис. 8.
Дифференцирующее звено
Уравнение движения для дифференцирующего звена имеет вид
![]()
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
![]()
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика дифференцирующего звена определяется как
![]() .
.
На рис. 9. приведена переходная характеристика дифференцирующего звена.
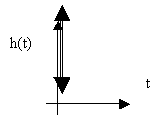
Рис. 9. Переходная характеристики звена
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
![]()
Исходя из этого, амплитудно-частотная характеристика звена определяется как:
![]()
Вещественная
![]() и
мнимая
и
мнимая
![]() частотные
характеристики звена определяются как
частотные
характеристики звена определяются как
![]() .
.
![]()
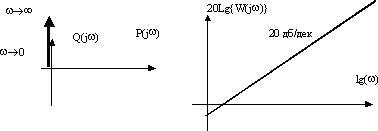
Рис. 10. Амплитудно-фазовая частотная и логарифмическая частотные характеристики звена
Выражение для расчета ЛАЧХ принимает вид:
![]()
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
![]() .
.
Амплитудно-фазовая и логарифмическая частотные характеристики звена показаны на рис. 10.
Колебательное звено
Уравнение движения для колебательного звена имеет вид
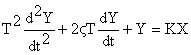 ,
,
где
![]() –
постоянная времени звена,
–
постоянная времени звена,
![]() —
коэффициент
демпфирования.
—
коэффициент
демпфирования.
Выполняя над этим уравнением преобразование Лапласа, получаем выражение для передаточной функции звена следующего вида:
![]()
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Корни характеристического уравнения звена определяются как:
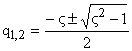
Для колебательного звена характерно различное распределение корней при разных комбинациях его параметров. В общем случае выражение переходная характеристика определяется выражением вида:
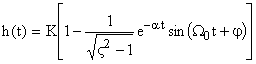 ,
,
где
![]() —
декремент затухания;
—
декремент затухания;
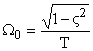 —
частота собственных колебаний;
—
частота собственных колебаний;
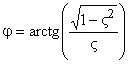 —
начальная фаза
колебаний
—
начальная фаза
колебаний
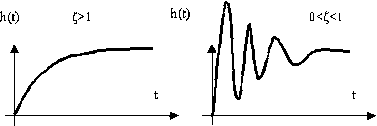
Рис. 11. Временные характеристики звена
Временные характеристики колебательного звена определяются распределением корней его характеристического полинома. На рис. 11 приведены переходные характеристики колебательного звена при действительно и комплексно-сопряженных корней характеристического полинома.
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:
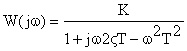
Исходя из этого, амплитудно-частотная характеристика колебательного звена определяется как:
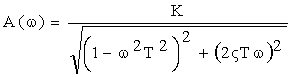
Вещественная
![]() и
мнимая
и
мнимая
![]() частотные
характеристики звена определяются как
частотные
характеристики звена определяются как
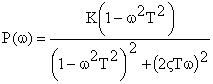 .
.
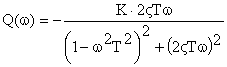
Выражение для расчета ЛАЧХ принимает вид:
![]()
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
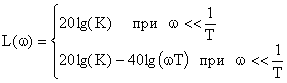 .
.
Амплитудно-фазовая и логарифмическая частотные характеристики звена показаны на рис. 12.
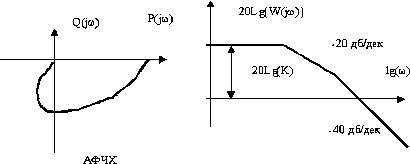
Рис. 12. Амплитудно-фазовая частотная и логарифмическая частотные характеристики колебательного звена
