17. Основные правила стандартизации психодиагностических методик.

091208-matmetody.txt

Стандартизацией психодиагностических методов называется процедура получения шкалы, позволяющей сравнивать индивидуальный результат по тесту с результатами большой группы.

с. 47 (54)

Тестовые шкалы разрабатываются для того, чтобы оценить индивидуаль­ный результат тестирования путем сопоставления его с тестовыми нормами, полученными на выборке стандартизации. Выборка стандартизации специаль­но формируется для разработки тестовой шкалы — она должна быть репре­зентативна генеральной совокупности, для которой планируется применять данный тест. Впоследствии при тестировании предполагается, что и тестиру­емый, и выборка стандартизации принадлежат одной и той же генеральной совокупности.

Исходным принципом при разработке тестовой шкалы является предпо­ложение о том, что измеряемое свойство распределено в генеральной сово­купности в соответствии с нормальным законом. Соответственно, измерение в тестовой шкале данного свойства на выборке стандартизации также должно обеспечивать нормальное распределение. Если это так, то тестовая шкала является метрической — точнее, равных интервалов. Если это не так, то свой­ство удалось отразить в лучшем случае — в шкале порядка. Естественно, что большинство стандартных тестовых шкал являются метрическими, что по­зволяет более детально интерпретировать результаты тестирования — с уче­том свойств нормального распределения — и корректно применять любые методы статистического анализа. Таким образом, основная проблема стандар­тизации теста заключается в разработке такой шкалы, в которой распределе­ние тестовых показателей на выборке стандартизации соответствовало бы нормальному распределению.

Исходные тестовые оценки — это количество ответов на те или иные воп­росы теста, время или количество решенных задач и т. д. Они еще называют­ся первичными, или «сырыми» оценками. Итогом стандартизации являются тестовые нормы — таблица пересчета «сырых» оценок в стандартные тестовые шкалы.

Существует множество стандартных тестовых шкал, основное назначение которых — представление индивидуальных результатов тестирования в удоб­ном для интерпретации виде. Некоторые из этих шкал представлены на рис. 5.5. Общим для них является соответствие нормальному распределению, а различаются они только двумя показателями: средним значением и мас­штабом (стандартным отклонением — о), определяющим дробность шкалы.

Общая последовательность стандартизации (разработки тестовых норм — таб­лицы пересчета «сырых» оценок в стандартные тестовые) состоит в следующем:

1. определяется генеральная совокупность, для которой разрабатывается методика и формируется репрезентативная выборка стандартизации;

2. по результатам применения первичного варианта теста строится рас­ пределение «сырых» оценок;

3. проверяют соответствие полученного распределения нормальному за­ кону;

4. если распределение «сырых» оценок соответствует нормальному, про­ изводится линейная стандартизация;

5. если распределение «сырых» оценок не соответствует нормальному, то возможны два варианта:

• перед линейной стандартизацией производят эмпирическую норма­ лизацию;

• проводят нелинейную нормализацию.

Проверка распределения «сырых» оценок на соответствие нормальному закону производится при помощи специальных критериев, которые мы рас­смотрим далее в этой главе.

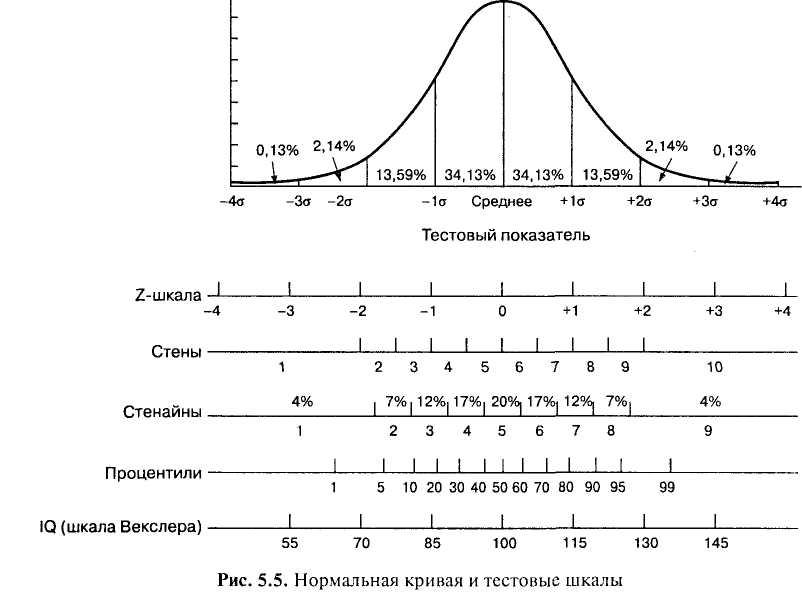
Линейная стандартизация заключается в том, что определяются границы интервалов «сырых» оценок, соответствующие стандартным тестовым пока­зателям. Эти границы вычисляются путем прибавления к среднему «сырых» оценок (или вычитания из него) долей стандартных отклонений, соответству­ющих тестовой шкале.

Тестовые нормы — таблица пересчета «сырых» баллов в стены

Стены	1	2	3	4	5	6	7	8	9	10
«Сырые» баллы	<11	11-13	14-16	17-19	20-22	23-25	26-28	29-31	32-34	>34

Пользуясь этой таблицей тестовых норм индивидуальный результат («сырой» балл) переводят в шкалу стенов, что позволяет интерпретировать выраженность измеря­емого свойства.

Эмпирическая нормализация применяется, когда распределение «сырых» баллов отличается от нормального. Она заключается в изменении содер­жания тестовых заданий. Например, если «сырая» оценка — это количе­ство задач, решенных испытуемыми за отведенное время, и получено рас­пределение с правосторонней асимметрией, то это значит, что слишком большая доля испытуемых решает больше половины заданий. В этом случае необходимо либо добавить более трудные задания, либо сократить время решения.

Нелинейная нормализация применяется, если эмпирическая нормализа­ция невозможна или нежелательна, например, с точки зрения затрат вре­мени и ресурсов. В этом случае перевод «сырых» оценок в стандартные про­изводится через нахождение процентильных границ групп в исходном распределении, соответствующих процентильным границам групп в нор­мальном распределении стандартной шкалы. Каждому интервалу стандарт­ной шкалы ставится в соответствие такой интервал шкалы «сырых» оценок, который содержит ту же процентную долю выборки стандартизации. Вели­чины долей определяются по площади под единичной нормальной кривой, заключенной между соответствующими данному интервалу стандартной шкалы г-оценками.

Например, для того чтобы определить, какой «сырой» балл должен соот­ветствовать нижней границе стена 10, необходимо сначала выяснить, какому г-значению соответствует эта граница (z = 2). Затем по таблице нормального распределения (приложение 1) надо определить, какая доля площади под нормальной кривой находится правее этого значения (0,023). После этого определяется, какое значение отсекает 2,3% наибольших значений «сырых» баллов выборки стандартизации. Найденное значение и будет соответство­вать границе 9 и 10 стена.

Изложенные основы психодиагностики позволяют сформулировать мате­матически обоснованные требования к тесту. Тестовая методика должна со­держать:

• описание выборки стандартизации;

• характеристику распределения «сырых» баллов с указанием среднего и стандартного отклонения;

• наименование, характеристику стандартной шкалы;

• тестовые нормы — таблицы пересчета «сырых» баллов в шкальные.