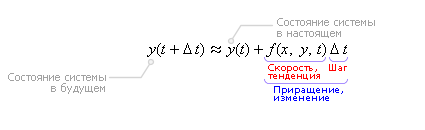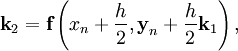- •1. Векторы и матрицы в matlab. Решение систем линейных уравнений. Функции matlab det(a), rank(a), rref(a), inv(a) .
- •1)Стандартные векторы:
- •2)Стандартные матрицы:
- •3) Операции над векторами и матрицами:
- •9) Обратная матрица:
- •8)Системы линейных уравнений. Существование и единственность решения
- •3. Тригонометрические ряды Фурье. Ряды Фурье в комплексной форме.
- •4. Интегральное преобразование Фурье
- •5. Дискретное преобразование Фурье, реализация в matlab. Функции fft(X) и ifft(X). Частота Найквиста.
- •6. Теорема в.А.Котельникова (теорема отсчетов).
- •8. Линейные системы. Передаточная функция.
- •Линейные стационарные системы
- •Дискретная передаточная функция
- •9. Ачх и фчх. Фильтры. Функции matlab: freqs(b,a), tf2zp(b,a), zp2tf(z,p,k), residue(b,a)
- •10. Цифровая фильтрация. Z-преобразование. Примеры фильтров. Функции matlab: freqz(b,a), residuez(b,a), filter(b,a,X), impz(b,a,n,f)
- •12. Стационарные случайные процессы. Корреляционная (ковариационная) функция и спектральная плотность стационарного случайного процесса.
12. Стационарные случайные процессы. Корреляционная (ковариационная) функция и спектральная плотность стационарного случайного процесса.
Стационарным называется сигнал, вероятностные характеристики которого не зависят от времени.
Корреляционная функция. Она характеризует стохастическую (случайную) связь между двумя мгновенными значениями случайного сигнала, разделенного заданным интервалом времени τ
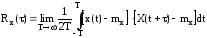 ;
;
Взаимная корреляционная функция. Она характеризует стохастическую связь мгновенными значениями случайных сигналов x(t) и y(t), разделенными интервалом времени τ
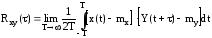 .
.
Корреляция (или ковариация) двух случайных величин показывает степень линейной зависимости этих величин друг от друга.
Для
случайных процессов вводят понятия
корреляционных и ковариационных функций,
аргументом которых в случае стационарных
СП является временной интервал
![]() ,
разделяющий два выборочных значения
случайных процессов. Если случайные
величины являются значениями одного и
того же СП, например, процесса
,
разделяющий два выборочных значения
случайных процессов. Если случайные
величины являются значениями одного и
того же СП, например, процесса
![]() ,
то указанная функция называется
автоковариационной
(или просто ковариационной);
она рассчитывается по формуле:
,
то указанная функция называется
автоковариационной
(или просто ковариационной);
она рассчитывается по формуле:
|
|
|
|
|
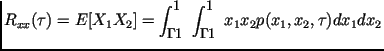
и
характеризует меру статистической
зависимости значений
![]() и
и
![]() ,
сдвинутых относительно друг друга на
интервал времени
,
сдвинутых относительно друг друга на
интервал времени
![]() .
Величина временного сдвига
.
Величина временного сдвига
![]() может
быть как положительной, так и отрицательной,
и меняется в пределах
может
быть как положительной, так и отрицательной,
и меняется в пределах
![]() .
.
Аналогично
автокорреляционная
(или просто корреляционная)
функция СП
![]() имеет
вид:
имеет
вид:
|
|
|
|
|
|
|
|
|
|
Если
же случайные величины принадлежат
разным случайным процессам, например,
![]() и
и
![]() ,
то функции называются взаимными
ковариационной и корреляционной,
рассчитываются по формулам:
,
то функции называются взаимными
ковариационной и корреляционной,
рассчитываются по формулам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и
характеризуют степень связанности
(взаимозависимости) двух СП
![]() и
и
![]() в
зависимости от временного сдвига
в
зависимости от временного сдвига
![]() .
.
Спектральная плотность такого процесса может быть найдена на основании теоремы Винера-Хинчина как преобразование Фурье от корреляционной функции:
|
В Матлабе: xcorr – взаимная корр. функция xcorr2 — расчет двумерной взаимной корреляционной функции xcov — расчет ковариационной функции csd — оценка взаимной спектральной плотности pburg — оценка спектральной плотности мощности методом Берга pcov — оценка спектральной плотности мощности ковариационным методом S = corrcoef(X) возвращает матрицу коэффициентов корреляции для двумерного массива, когда каждый столбец рассматривается как переменная, а каждая строка - как наблюдение.
13. Прохождение случайного сигнала через линейную систему (фильтр). Случайные сигналы — сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. В качестве примера рассмотрим гармонический сигнал со случайной начальной фазой. Во многих практических задачах используется модель случайного процесса, реализации которого представляют собой гармонические колебания с известными (детерминированными) амплитудой и частотой, но случайной начальной фазой. Таким образом, реализация рассматриваемого случайного процесса может быть записана как: x(t)=A*cos(ω0*t+φ), где А амплитуда (детерминированная), ω0 — частота(детерминированная), и φ — случайная начальная фаза, которая в большинстве практически интересных случаев может считаться равномерно распределённой на интервале 0…2π, то есть имеющей следующую плотность вероятности:
Графики нескольких реализаций данного случайного процесса, представляющие собой смещённые друг относительно друга по временной оси синусоиды.Как видим, конкретный вид реализации процесса в данном случае определяется значением всего лишь одной случайной величины: начальной фазы. Случайные процессы, конкретный вид реализаций которых определяется значениями конечного числа параметров (случайных величин), называют квазидетерминированными случайными процессами.
14. Процесс случайного блуждания. Модели ARIMA. Случайный процесс специального вида, исторически связанный с моделью перемещения частицы под действием некоторого случайного механизма в произвольном фазовом пространстве. Обычно рассматривается случайное блуждание, порождаемое суммами взаимно независимых одинаково распределённых величин X1, X2, ..., Xnили цепями Маркова. Пусть S0=0, Sn= X1 + X2 + ... + Xn, тогда последовательность координат (n, Sn), n=0, 1, 2, ..., описывает траекторию случайного блуждания. Основные черты общих случайных блужданий можно охарактеризовать на примере простейшего случайного блуждания, порождаемого схемой испытаний Бернулли. Описание случайного блуждания принято в терминах частицы, которая движется по точкам вида k (k - целое) оси x. Движение начинается в момент t = 0, и положение частицы меняется только в дискретные моменты времени 0, 1, 2, ... На каждом шаге координата частицы увеличивается или уменьшается на величину 1 с вероятностями p и q = p-1, соответственно, независимо от предшествующего движения. Обычно случайные блуждания изображают геометрически, беря ось t за ось абсцисс, а ось x - за ось ординат. Пусть Xj - случайная величина, равная величине перемещения частицы на j-м шаге, т. е. X1 = 1 с вероятностью p и X1 = -1 с вероятностью q. Тогда X1, X2, ..., Xn, ... образуют последовательность независимых бернуллиевских случайных величин. параметрические модели стационарных случайных процессов — модели авторегрессии и скользящего среднего. Пусть Xt — значения стационарного случайного процесса, =EXt, xt=Xt-. Введем случайный процесс (t) N(0,2), для которого Et=0, Dt=2, Ett+=0 (0). Случайный процесс t будем называть белым шумом. Модель AR(1) авторегрессии первого порядка имеет вид xt= a xt-1+ξt, (12.1) где |a|<1 — необходимое условие стационарности процесса xt. В случае a=1 получаем модель случайного блуждания xt=xt-1+ξt. (12.2) Временной ряд (12.2) является нестационарным. Пусть x0=0. Тогда Ext=0, Dxt=2t, а для стационарного процесса дисперсия не должна зависеть от времени t. Допустим, что для модели (12.1) дисперсия постоянна: Dxt=x2. Тогда из формулы (12.1) следует, что
Наши вычисления показывают, что действительно, процесс авторегрессии первого порядка стационарен только при условии |a|<1. При этом надо дополнительно потребовать, чтобы начальное значение x0 было случайной величиной, причем Ex0=0, Dx0=x2. Если же исходить из фиксированного (неслучайного) значения x0=0, то можно показать, что значение дисперсии (12.3) устанавливается в пределе при t∞. Модель AR(2) авторегрессии второго порядка определяется формулой xt=a1xt-1+ a2xt-2+ξt . (12.4) Условие стационарности в этом случае сводится к требованию, чтобы корни (в общем случае комплексные) уравнения 1- a1z-1 - a2z-2=0 (12.5) удовлетворяли условию |z|<1.
15. Интерполяционный полином Лагранжа. Интерполяция многочленами в MATLAB. Функции polyfit(x,y,n), polyval(pn,x) Интерполяцио́нный
многочле́н Лагра́нжа — многочлен минимальной
степени, принимающий данные значения
в данном наборе точек. Для n +
1 пар чисел Лагранж предложил
способ вычисления таких многочленов:
где базисные полиномы определяются по формуле:
lj(x) обладают следующими свойствами:
Отсюда следует, что L(x), как линейная комбинация lj(x), может иметь степень не больше n, и L(xj) = yj, Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n +1, содержащая коэффициенты аппроксимирующего полинома. y = polyval(p, s) Y = polyval(p, S) Функция y = polyval(p, s), где p = [p1 p2 ... pn pn+1] - вектор коэффициентов полинома p(x) = p1xn + p2xn-1 + ... + pnx + pn+1, вычисляет значение этого полинома в точке x = s. Функция Y = polyval(p, S), где S - одномерный или двумерный массив, вычисляет значение этого полинома для каждого элемента массива, поэтому size(Y) = size(V). Вычислим значение полинома p(x) = 3x2 + 2x +1 в точке x = 5. p = [3 2 1] p = 3 2 1 y = polyval(p, 5) y = 86
16. Метод наименьших квадратов: случай парной регрессии. Реализация МНК в EXCEL. Функция «ЛИНЕЙН». Пусть имеется n пар чисел (xi,yi), i=1,2,…,n, относительно которых предполагается, что они отвечают линейной зависимости между величинами x и y: y=a+bx , возможно, с некоторой ошибкой i, так что yi=a+bxi+i, i=1,2,…,n . (4.1) Какими
должны быть наилучшие значения
параметров a
и b?
Применяя метод
наименьших квадратов,
мы требуем, чтобы сумма квадратов
ошибок i
была наименьшей:
Необходимым условием минимума этой функции, как известно, является равенство нулю ее частных производных по a и b:
ЛИНЕЙН(Значения_y; Значения_x; Конст; статистика) Значения_y - массив значений y.Значения_x- необязательный массив значений x, если массив х опущен, то предполагается, что это массив {1;2;3;...} такого же размера, как иЗначения_y.Конст - логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если Конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если аргумент Конст имеет значение ЛОЖЬ, то b полагается равным 0 и значения a подбираются так, чтобы выполнялось соотношение y = ax.Статистика - логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если аргумент статистика имеет значениеЛОЖЬ или опущен, то функция ЛИНЕЙН возвращает только коэффициент a и постоянную b.
17. Метод наименьших квадратов: случай множественной регрессии. Реализация МНК в EXCEL. Функция «ЛИНЕЙН». На опыте получены значения x и y, сведенные в таблицу
по методу наименьших квадратов. Решение.
91a+21b=179,1, 21a+6b=46,3, a=0,98 b=4,3.
где m - число учитываемых факторов (независимых переменных), n - объем выборки.
18. Статистические аспекты метода наименьших квадратов: статистические свойства оценок, коэффициент детерминации R2.
Коэффициент детерминации R2 характеризует качество регрессионной модели. R2[0,1] и чем меньше R2 отличается от 1, тем лучше регрессионная модель.
20. Линейные операторы. Линейные преобразования. Ортогональные преобразования Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу L по некоторому правилу ставится в соответствие элемент А L. Преобразование А называется линейным, если для любых векторов L и L и любого верно: A(+) = A+A A() = A Линейное преобразование называется тождественным, если оно преобразует элемент линейного пространства сам в себя. Пример. Является ли А линейным преобразованием. А=+; 0.Запишем преобразование А для какого- либо элемента . А = + Проверим, выполняется ли правило операции сложения для этого преобразования А(+) = ++; A() + A() = +++, что верно только при = 0, т.е. данное преобразование А нелинейное. Если в пространстве L имеются векторы линейного преобразования , то другой векторявляется линейной комбинацией векторов . Если только при = = … = = 0, то векторы называются линейно независимыми. Если в линейном пространстве L есть n линейно независимых векторов, но любые n + 1 векторов линейно зависимы, то пространство L называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства L. Следствие: Любой вектор линейного пространства может быть представлен в виде линейной комбинации векторов базиса Ортогональное преобразование — линейное преобразование евклидова пространства, сохраняющее длины или (что эквивалентно этому) скалярное произведение векторов. -Ортогональные преобразования и только они переводят ортонормированный базис в ортонормированный. - Необходимым и достаточным условием ортогональности является также равенство , где — сопряженное, а — обратное линейные преобразования. -В ортонормированном базисе ортогональные преобразования (и только им) соответствуютортогональные матрицы. - Собственные значения ортогональных преобразований равны по модулю , а собственные векторы, отвечающие различным собственным значениям, ортогональны. - Определитель ортогонального преобразования равен (собственное ортогональное преобразование) или (несобственное ортогональное преобразование). - В произвольном -мерном евклидовом пространстве ортогональное преобразование является композицией конечного числа отражений. -Множество всех ортогональных преобразований евклидова пространства образует группу относительно операции композиции — ортогональную группу данного евклидова пространства. -Собственные ортогональные преобразование образуют нормальную подгруппу в этой группе (специальную ортогональную группу).
21. Задача на собственные значения. Функция MATLAB [V,D]=eig(A). Вектор х (ненулевой) называется собственным вектором квадратной матрицы А, если Ах=lх для некоторого числа l, которое называется собственным числом м. А, соответсвующим собственному вектору х. Любой вектор kх также является собственным вектором для того же собственного числа l. Собственные числа м. А являются корнями характеристического уравнения det(А-lЕ)=0. Его левая часть h(l)=det(A-lE) называется характеристическим полиномом. Его степень равна порядку матрицы А. Наличие и количество собственных чисел матрицы зависит от того, над каким полем она рассматривается. Если это мн-во вещественных чисел, то комплексные корни характеристического уравнения игнорируются. В матлабе функция eig: Функция d = eig(A) вычисляет собственные значения матрицы A. Функция [R, D] = eig(A) вычисляет диагональную матрицу D собственных значений и матрицу R правых собственных векторов, удовлетворяющих соотношению A * R = R * D. Эти векторы нормированы так, что норма каждого из них равна единице. Левые собственные векторы могут быть найдены следующим образом: [L, D] = eig(A’); Матрицы собственных значений D для A и A’ содержат одни и те же собственные значения, хотя порядок их следования может быть различен. Матрица левых собственных векторов удовлетворяет соотношению A’ * L = L * D. Для согласования независимо найденных систем правых и левых собственных векторов систему левых векторов необходимо нормировать так, чтобы соблюдалось условие L * R = eye(n,n). Функция [R, D] = cdf2rdf(R, D) преобразовывает комплексные выходы функции eig в действительные, при этом комплексные собственные значения преобразовываются в блоки размера 2 х 2, а комплексная матрица правых собственных векторов R преобразовывается в действительную, столбцы которой, соответствующие действительным собственным значениям, сохраняются, а соответствующие комплексным - расщепляются на два: [Re(ri) Im(ri)].
22. Норма вектора и норма матрицы. Число обусловленности. Функции MATLAB norm(A), cond(A). Норма — функция, заданная на векторном пространстве и обобщающая понятие длины вектора или абсолютного значения числа. Норма вектора
Норма в векторном
пространстве
Эти условия являются аксиомами нормы. Векторное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства.
Чаще всего норму
обозначают в виде:
Вектор с
единичной нормой (
Любой ненулевой
вектор x можно нормировать,
то есть разделить его на свой модуль:
вектор Норма матрицы
Нормой матрицы A называется вещественное
число
Если выполняется также и четвёртое свойство, норма называется мультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы мультипликативны. Немультипликативные нормы для матриц являются простыми нормами, заданными в линейных пространствах матриц.
Матричная
норма
для всех число обусловленности Пусть задан ограниченный обратимый линейный оператор A. характеризует точность решения задачи и является мерой аменабельности этого решения в численном представлении, то есть насколько задача хорошо или плохо обусловлена.
Если
оператор
Описание: Нормы векторов: Функция n = norm(v, p) вычисляет p-норму вектора v, определяемую следующим образом: || v ||p = sum(abs(v).^p)^1/p. Cправедливы следующие соотношения: norm(v) = norm(v, 2); norm(v, inf) = max(abs(v)); norm(v, -inf) = min(abs(v)). Нормы матриц: Функция n = norm(A, p) вычисляет подчиненную p-норму матрицы A только для значений p, равных 1, 2, inf. Cправедливы следующие соотношения: norm(A, 1) = max(sum(abs(A))); norm(A, inf) = max(sum(abs(A’))); norm(A, ‘fro’) = sqrt(sum(diag(A’ * A))); norm(A) = norm(A, 2) = smax(A). Пример:
k = cond(A) Описание: Функция k = cond(A) возвращает число обусловленности матрицы A по отношению к операции обращения, которое равно отношению максимального сингулярного числа к минимальному: k = max/ min. Число обусловленности по отношению к операции обращения - это мера относительной погрешности, равная k = ||(A-1)||/||A||, где ||A|| - норма матрицы погрешностей исходных данных. Оно характеризует точность операции обращения матрицы или решения системы линейных уравнений. Эта функция неприменима для разреженных матриц
23. Сингулярное разложение матрицы. Псевдообратные матрицы. Метод наименьших квадратов. Функция MATLAB [U,D,V]=svd(A).
Любая матрица M
порядка
Псевдообратные матрицы A + называется псевдообратной матрицей для матрицы A, если она удовлетворяет следующим критериям:AA + A = A;A + AA + = A + (A + является слабым обращением в мультипликативной полугруппе);(AA + ) * = AA + (это означает, что AA + — эрмитова матрица);(A + A) * = A + A (A + A — тоже эрмитова матрица).Здесь M * — эрмитово сопряжённая матрица M (для матриц над полем действительных чисел M * = MT). Свойства:Псевдообращение обратимо, более того, эта операция обратна самой себе:
(A + ) + =
A.Псевдообращение коммутирует с
транспонированием, сопряжением и
эрмитовым сопряжением:(AT) + = (A + )T, Псевдообратное произведения матрицы A на скаляр α равно соответствующему произведению матрицы A + на обратное число α - 1:(αA) + = α − 1A + , для α ≠ 0. Если псевдообратная матрица для A * A уже известна, она может быть использовано для вычисления A + :A + = (A * A) + A * .Аналогично, если матрица (AA * ) + уже известна: A + = A * (AA * ) + . Метод наименьших квадратов –регрессионный анализ разность между настоящим значением, и предсказанным моделью
сумма квадратов этих разностей минимально
s = svd(A) [U, S, V] = svd(A) [U, S, V] = svd(A, 0) Если A - действительная матрица размера m х n (m >= n), то ее можно представить в виде [1]: A = U * S * VT,где UTU = V * VT = In и S = diag(s1, ...sn). Такое разложение называется сингулярным разложением матрицы A.Матрица U сформирована из n ортонормированных собственных векторов, соответствующих n наибольшим собственным значениям матрицы AAT, а матрица V - из ортонормированных собственных векторов матрицы ATA. Диагональные элементы матрицы S - неотрицательные значения квадратных корней из собственных значений матрицы ATA; они называются сингулярными числами.Допустим, что s1>= s2 >=... >= sn >= 0. Если ранг матрицы A равен r, то значения sr+1 = sr+2 = ... = sn = 0.Существует другое, более экономное сингулярное разложение: A = Ur * Sr * VrT,где UrTUr = Vr * VrT = Ir и Sr = diag(s1, ..., sr).Функция s = svd(A) вычисляет только сингулярные числа матрицы A.Функция [U, S, V] = svd(A) вычисляет диагональную матрицу S тех же размеров, которые имеет и матрица A с неотрицательными диагональными элементами в порядке их убывания, а также унитарные матрицы преобразований U и V.Функция [U, S, V] = svd(A, 0) выполняет экономное сингулярное разложение. Пример 1: Рассмотрим прямоугольную матрицу размера 4 х 2. A =
Полное сингулярное разложение [U, S, V] = svd(A)
24. Численное дифференцирование. Разностные формулы для производных первого и второго порядков, их спектральный анализ.
Пусть имеется
функция Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно его заменить более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных ввобще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования. Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции приближенного заменяется соответствующей производной интерполяционного многочлена
Рассмотрим простейшие формулы численного дифференцирования, которые получаются указанным способом. Будем предполагать, что функция задана в равностоящих узлах
Построим интерполяционный многочлен первой степени
Производная
Производную
функцию
Величина
Пусть Интерполяционный многочлен Ньютона второй степени имеет вид
Берем производную
В точке
Получаем приближенную формулу
Величина Наконец, если взять вторую производную
Величина Формулы (1)-(3) называются формулами численного дифференцирования.
Предполагая
функцию
25. Численное интегрирование: формулы прямоугольников, трапеций, Симпсона. Функции MATLAB: quad (‘f ’,a,b), dblquad(‘f ’,x1,x2,y1,y2) Суть: интеграл, считаем площадь под графиком Метод прямоугольников
Пусть требуется
определить значение интеграла функции
на отрезке
Метод трапеций Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций. Площадь трапеции на каждом отрезке:
Метод парабол (метод Симпсона) Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид
Функция quad(f,a,b) вычисляет интеграл по формулам Симпсона quad('sin(x)',0,1) Функция dblquad(f,a1,b1,a2,b2) вычисляет двойной интеграл
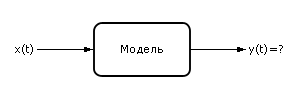
26. Численные методы интегрирования обыкновенных дифференциальных уравнений: метод Эйлера, метод Рунге-Кутта. Функция MATLAB: [t,y]=ode45(‘f ’,tlist,y0). Пусть нам известна входная динамическая последовательность X (входной сигнал) и модель (способ преобразования входного сигнала в выходной сигнал). Рассматривается задача определения выходного сигнала y(t) (см. рис. 10.1).
Модель динамической системы может быть представлена дифференциальным уравнением. Основное уравнение динамики: y' = f(x(t), y(t), t). Известны начальные условия в нулевой момент времени t0: y(t0), x(t0). Чтобы определить выходной сигнал, заметим, что по определению производной:
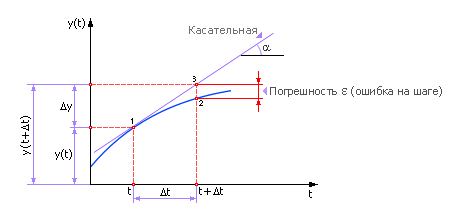
Нам известно положение системы в точке «1», требуется определить положение системы в точке «2». Точки отделены друг от друга расстоянием Δt (рис. 10.2). То есть расчет поведения системы производится по шагам. Из точки «1» мы скачком (дискретно) переходим в точку «2», расстояние между точками по оси t называется шагом расчета Δt.
Тогда:
или
Последняя формула называется формулой Эйлера. Очевидно, чтобы узнать состояние системы в будущем y(t + Δt), надо к настоящему состоянию системы y(t) прибавить изменение Δy, прошедшее за время Δt. метод Эйлера - самый простой Пусть дана задача Коши для уравнения первого порядка
где функция f определена
на некоторой области
Приближенное решение в узлах xi, которое обозначим через yi определяется по формуле
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
метод Рунге-Кутта - продвинутый, можно выбирать точность Рассмотрим задачу Коши
Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:
где h — величина шага сетки по x и вычисление нового значения проходит в четыре стадии:
Этот метод имеет четвёртый порядок точности, т.е. суммарная ошибка на конечном интервале интегрирования имеет порядокO(h4) (ошибка на каждом шаге порядка O(h5)).
Функция MATLAB: рунге кутта 4 и 5 порядка точности [t, X] = ode45(‘<имя функции>‘, t0, tf, x0) ‘<имя функции>‘ - строковая переменная, являющаяся именем М-файла, в котором вычисляются правые части системы ОДУ; t0 - начальное значение времени; tf - конечное значение времени; x0 - вектор начальных условий;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

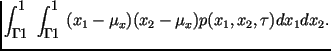
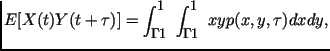
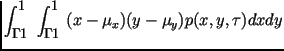
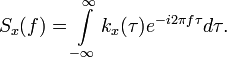
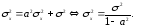 (12.3)
(12.3)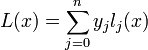
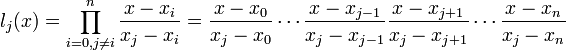
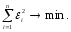 (4.2)Подставляя значения i
из (4.1) в (4.2), получим функцию
(4.2)Подставляя значения i
из (4.1) в (4.2), получим функцию
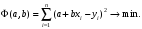
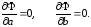
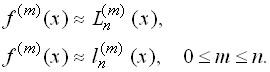
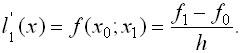
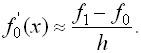 (1)
(1)
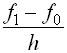 называется первой разностной
производной.
называется первой разностной
производной.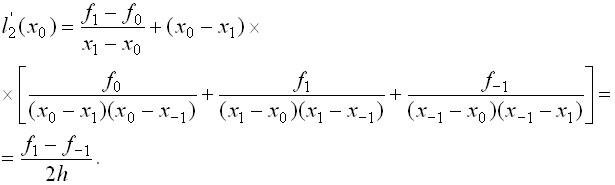
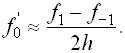 (2)
(2)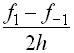 называется центральной
разностной производной.
называется центральной
разностной производной.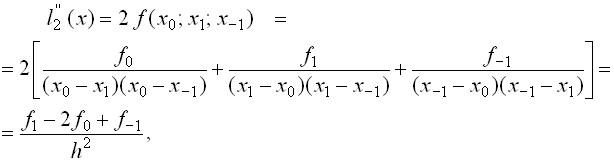 получаем
приближенную формулу.
получаем
приближенную формулу.  (3)
(3)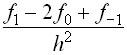 называется
второй разностной производной.
называется
второй разностной производной.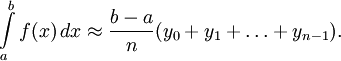
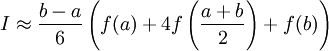 .
.