MathCad_программ_10_06_15 / методичка

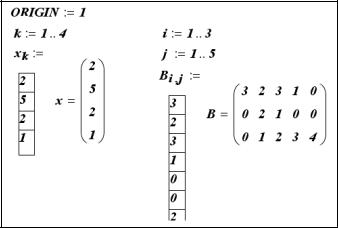
Решение. Конструкции, осуществляющие формирование требуемого вектора и матрицы, показаны на рис. 3.5.

Рис. 3.5. Ввод элементов массивов с клавиатуры

Заметим, что ввод элементов матрицы осуществляется построчно, т.е. первоначально вводятся элементы первой строки, затем – второй и т.д. Это обусловлено тем, что переменная i – номер строки является параметром внешнего цикла. Заметим, что на рис. 3.5 показаны не все вводимые элементы массива В (вводятся 15 элементов).

3.3.Верхний индекс массива

Внекоторых задачах обработки массивов возникает необходимость выделить определенный столбец. Для эффективного выполнения такого выделения массивы MathCAD могут иметь верхний индекс. Верхний индекс позволяет обращаться к отдельному столбцу массива.

53

Чтобы ввести верхний индекс, необходимо ввести имя массива, а затем нажать клавиши Ctrl 6 или щелкнуть на кнопке

палитры инструментов Matrix. Затем в появившихся угловых скобках ввести номер выделяемого столбца (с учетом значения системной переменной ORIGIN).

Пример 3.3.1. Из второго и четвертого столбца матрицы В примера 3.2.2 сформировать векторы c, d .

Решение. Конструкции, формирующие эти векторы, приведены на рис. 3.6.

Рис. 3.6. Использование верхнего индекса массива

3.4. Основные функции обработки массивов

Пакет MathCAD содержит большой набор встроенных функций, позволяющих возвращать различные характеристики массивов, создавать новые матрицы и преобразовывать существующие, обрабатывать массивы и облегчающих решение широкого круга задач линейной алгебры.

Вызов функций осуществляется выполнением пунктов меню Insert/Functions и в появившемся диалоговом окне выбирается нужная категория функций (для обработки массивов это

Vector and Matrix), а затем из правого списка Function Name вы-

бирается конкретная функция обработки массива (рис. 3.7). В нижней части окна выводится краткая информация о параметрах выбранной функции и ее назначении. Заметим, что обращение к функции можно ввести с клавиатуры.

Ниже приводится список встроенных функций, часто используемых для обработки массивов и разделенных на группы по назначению функций.

54

Рис. 3.7. Встроенные векторные и матричные функции

Функции определения характеристик массива. Эти функ-

ции вычисляют размеры массива и диапазон изменения его элементов. Имена и назначение функций приведены в табл. 3.1.

Таблица 3.1

55

Пример 3.4.1. Использование функций из табл. 3.1 показано на рис. 3.8.

Рис. 3.8. Вычисление характеристик массивов

Формирование матриц специального типа. Встроенные функции MathCAD, осуществляющие формирование матриц специального вида, приведены в табл. 3.2.

Таблица 3.2

56

Пример 3.4.2. Формирование матриц специального типа с использованием функций из табл. 3.2 показано на рис. 3.9.

Рис. 3.9. Формирование специального типа матриц

Заметим, что значение системной переменной ORIGIN в этом фрагменте равно 0. Докажите это, используя определение матрицы М и формирование вектора b.

Формирование новых массивов из существующих. Функ-

ции MathCAD для формирования новых массивов из существующих массивов приведены в табл. 3.3.

57

Пример 3.4.3. Используя функции табл. 3.3, сформировать новые матрицы из матриц, приведенных на рис. 3.10.

Решение. Первоначально сформируем исходные матрицы, показанные на рис. 3.10. Затем сформируем новые матрицы, приведенные на рис. 3.11.

Рис. 3.10. Формирование исходных матриц

Специальные характеристики матрицы. К специальным характеристикам матрицы можно отнести функции, определяющие такие характеристики матриц, как след, ранг, нормы и другие величины, через элементы исходной матрицы. Некоторые функции MathCAD приведены в табл. 3.4.

58

Пример 3.4.4. Вычислить специальные характеристики матриц D, M , элементы которых приведены на рис. 3.12.

Решение. Вычисление характеристик показано на рис. 3.12.

Рис. 3.12. Вычисление специальных характеристик матриц

3.5. Вычисления с массивами

Над векторами и матрицами можно производить вычисления в точности так же, как и над числами. Некоторые из операторов MathCAD имеют особые значения в применении к векторам и матрицам. Например, символ умножения означает просто умножение, когда применяется к двум числам, но он же означает скалярное произведение, когда применяется к векторам, и умножение матриц – когда применяется к матрицам.

В табл. 3.5. представлены векторные и матричные операторы MathCAD. Многие из этих операторов доступны из соответствующих палитр инструментов. Отметим, что операторы, которые имеют в качестве аргумента вектор, требуют вектор-

столбец, а не вектор-строку.

Операторы, не перечисленные в этой таблице, не будут работать для векторов и матриц. При попытке использовать такой оператор с вектором или матрицей MathCAD будет отмечать это сообщением об ошибке «неверная операция с массивом», или

«нескалярная величина». Используя оператор векторизации,

60

можно выполнить любую скалярную операцию или функцию поэлементно с вектором или матрицей.

Введем следующие обозначения: для матриц – A и M, для векторов – v и u и для скалярных величин – z.

61

62