Вычитание векторов

Вектор называется противоположным вектору , если их сумма равна нулевому вектору: . Противоположный вектор имеет длину , коллинеарен и противоположно направлен вектору (рис.1.8,а,б). Нулевой вектор является противоположным самому себе.

Разностью векторов и называется сумма вектора с вектором , противоположным вектору :

Для нахождения разности векторов и приложим к произвольной точке векторы и , а также вектор , противоположный вектору (рис.1.9,а). Искомую разность находим по правилу параллелограмма

Для нахождения разности проще использовать правило треугольника (рис. 1.9,6). Для этого прикладываем к произвольной точке векторы и . Вектор при этом равен искомой разности

Вычитание векторов — действие, обратное сложению — можно определить также следующим образом: разностью векторов и называется такой вектор , который в сумме с вектором дает вектор (рис.1.9,в), т.е. разность — это решение линейного векторного уравнения .

Решение. Учитывая равенство , получаем по правилу треугольника .

Поскольку и , то .

По правилу параллелограмма . Так как и , находим

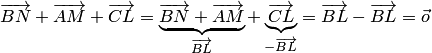
Умножение вектора на число

Произведением ненулевого вектора на действительное число называется вектор , удовлетворяющий условиям:

1) длина вектора равна , т.е. ;

2) векторы и коллинеарные ;

3) векторы и одинаково направлены, если , и противоположно направлены, если .

Произведение нулевого вектора на любое число считается (по определению) нулевым вектором: ; произведение любого вектора на число нуль также считается нулевым вектором: . Из определения произведения следует, что:

а) при умножении на единицу вектор не изменяется: ;

б) при умножении вектора на получается противоположный вектор: ;

в) деление вектора на отличное от нуля число сводится к его умножению на число , обратное .

г) при делении ненулевого вектора на его длину, т.е. при умножении на число получаем единичный вектор, одинаково направленный с вектором .

Действительно, длина вектора равна единице: .

Вектор коллинеарен и одинаково направлен с вектором , так как ;

д) при умножении единичного вектора на число получаем коллинеарный ему вектор, длина которого равна .

вектора на и , а также противоположный вектор .

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов , , и любых действительных чисел справедливы равенства:

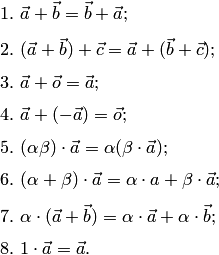
Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.

Линейные комбинации векторов

Применяя линейные операции, можно составлять суммы векторов, умноженных на числа.

Вектор называется линейной комбинацией векторов , если он может быть представлен в виде

,

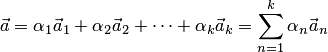где — некоторые числа. В этом случае говорят, что вектор разложен по векторам , а числа называют коэффициентами разложения.

Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Отметим следующие свойства линейных комбинаций векторов:

1. Если векторы — коллинеарны, то любая их линейная комбинация им коллинеарна.

2. Если векторы — компланарны, то любая их линейная комбинация им компланарна.

Докажем, например, первое свойство. При умножении вектора на число получаем (по определению) вектор, колпинеарный данному. При сложении двух векторов, параллельных некоторой прямой, получаем (по определению) вектор, параллельный той же самой прямой. Поэтому линейная комбинация двух коллинеарных векторов и коллинеарна им. По индукции свойство распространяется на любое конечное число коллинеарных векторов.

Аналогично доказывается второе свойство.